《电路基础》第八章学习笔记
本章学习二阶电路,典型是RLC电路。电路中包含三种无源元件(两种储能元件)。可以用二阶微分方程表征其特性。
-
初值与终值的确定
-
关键点:
-
分析电路时,必须始终仔细地处理电容器两端电压v(t)的极性以及流过电感器电流i(t) 的方向,v与i必须严格按照无源符号规约予以定义。
-
电容两端的电压总是连续的
\[v(0^+)=v(0^-) \] -
流过电感的电流总是连续的
\[i(0^+)=i(0^-) \] -
电容和电感是破局关键。分析的时候从这两个下手更简明。
-
-
-
无源激励RLC串联电路
-
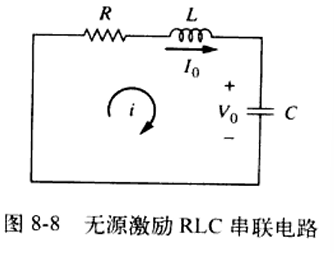
对上图运用KVL,得到:
\[Ri+L\frac{\mathrm{d}i}{\mathrm{d}t } +\frac{1}{C}\int_{-\infty}^{t} i\mathrm{d}t =0 \]对这个式子中的 t 求导:
\[\frac{\mathrm{d^2}i }{\mathrm{d}t^2 }+\frac{R}{L}\frac{\mathrm{d}i }{\mathrm{d}t }+\frac{i}{LC}=0 \]这是一个二阶微分方程。
初值带入后化简运算,进一步得到:
\[s^2+\frac{R}{L}s+\frac{1}{LC}=0 \]这是一个一元二次方程,我们可以通过求根公式求出解的答案。
-
两个根的更简洁的表达式可以写成:
\[s_{1}=-\alpha +\sqrt{\alpha ^2-\omega _{0}^2} ,s_{2}=-\alpha -\sqrt{\alpha ^2-\omega _{0}^2} \]其中,
\[\alpha =\frac{R}{2L},\omega _{0}=\frac{1}{\sqrt{LC}} \]-
特征根 \(s_{1}\) 和 \(s_{2}\) 与电路的自然相应有关,称为自然频率
-
\(\omega_{0}\) 称为振荡频率/无阻尼自然频率
-
\(\alpha\) 称为奈培频率/阻尼因子
-
上面的一元二次方程可以简写为:
\[s^2+2\alpha s+\omega _{0}^2=0 \]这样就简单舒服多了!
-
-
解的三种情况:
-
过阻尼(\(\alpha>\omega_{0}\))
\[i(t)=A_{1}e^{s_{1}t}+A_{2}e^{s_{2}t} \] -
临界阻尼(\(\alpha=\omega_{0}\))
\[i(t)=(A_{2}+A_{1}t)e^{-\alpha t} \] -
欠阻尼(\(\alpha<\omega_{0}\))
\[i(t)=e^{-\alpha t}(B_{1}cos\omega_{d}t+B_{2}sin\omega_{d} t) \]
-
-
RLC网络的性质:
- 特征:阻尼衰减
- 由于两类储能元件的存在,振荡响应成为可能(LC振荡电路)
- 不同情况下响应的波形是不同的。
-
-
无源激励RLC并联电路
-

对上图顶点KCL之后化简可得:
\[s^2+\frac{1}{RC}s+\frac{1}{LC}=0 \]剩下的同上面串联电路进行分析,就不过多展开了。
-
-
RLC串联电路的阶跃响应
-
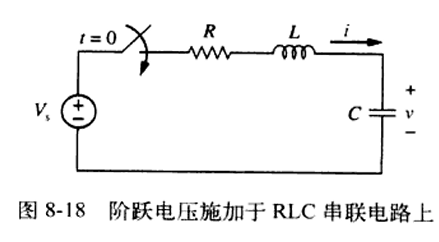
对这个电路使用KVL,化简之后得到:
\[\frac{\mathrm{d^2}v }{\mathrm{d}t^2 }+\frac{R}{L}\frac{\mathrm{d}v }{\mathrm{d}t }+\frac{v}{LC}=\frac{V_{s}}{LC} \] -
上式的解包含:瞬态响应与稳态响应
\[v(t)= v_{1}(t)+v_{ss}(t) \]所以过阻尼,欠阻尼,临界阻尼的全解:在 \(A_{1},A_{2}\) 的表达式中加入 \(V_{s}\)
-
-
RLC并联电路的阶跃响应
-
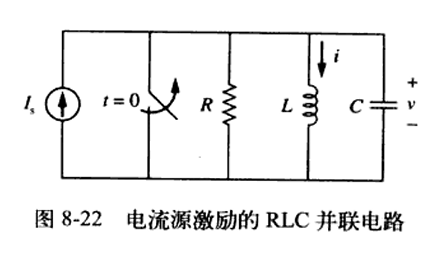
对顶部节点使用KCL得到:
\[\frac{\mathrm{d^2}i }{\mathrm{d}t^2 }+\frac{1}{RL}\frac{\mathrm{d}i }{\mathrm{d}t }+\frac{i}{LC}=\frac{I_{s}}{LC} \]上式的解包含:瞬态响应与稳态响应
\[x(t)= x_{1}(t)+x_{ss}(t) \]所以过阻尼,欠阻尼,临界阻尼的全解:在 \(A_{1},A_{2}\) 的表达式中加入 \(I_{s}\)
-
-
一般二阶电路
-
分析方法:(重要)😄
-
确定电路的初始条件以及终值
-
关闭独立源,用KCL和KVL求解瞬态响应 \(x_{1}(t)\) 。得到二阶微分方程就可以求出特征根。
-
电路的稳态响应为:
\[x_{ss}(t)=x(\infty) \] -
电路的全响应即瞬态响应与稳态响应之和。
-
-
-
对偶原理(互换关系)
-
内容:
对偶原理指出了电路的特征方程与电路原理之间存在的对偶关系。

如果两个电路能够用对偶量可相互交换的相同的特征方程来描述,则称这两个电路时互为对偶的。
-
有效性:
只要求出一个电路的解,就可以自动推出其对偶电路的解。
-
如何得到一个电路的对偶电路:
- 在给定电路的各网孔中心设置一个节点,在该给定电路之外设置对偶电路的参考节点(GND)
- 在节点之间画线,使每条线通过一个元件,并将该元件用其对偶元件取代。
- 对于引起正的(顺时针方向)网孔电流的电压源而言,其对偶电流源的参考方向为地节点流向非参考节点。
-
呼,终于结束了,再记电路笔记要患上腱鞘炎了。
typora记笔记真的磨人,但是阅读的时候感觉特别清晰+美观。
latex还是敲太慢了。
笔记任务完成了,多做习题巩固,常看常新。
这本书写的真好。如果有纸质版就更好了,可惜买不到。
2025.10.3
