一.题面:
点这里
二.分析:
1.性质分析:
首先,对于题目中复杂的过程描述,我们应当找到生成新图的本质。
考虑对于第 \(i\) 次操作的意义,通过点 \(u\) 生成了一个全新的点 \(u'\),然后对于 \(\forall_{v\in V(u)}\) ,如果 \(v'\) 不存在,生成无向边 \((v,u')\) ,如果 \(v'\) 存在,则生成无向边 \((v',u')\)。
那么基于这个描述,我们可以手动模拟此过程。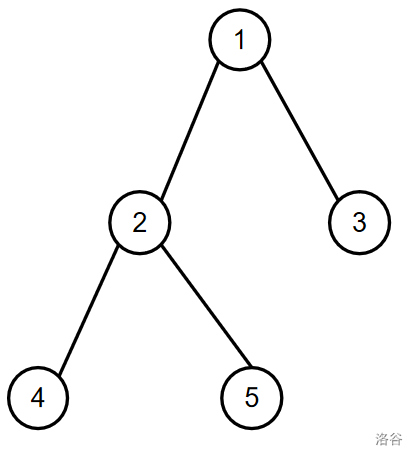
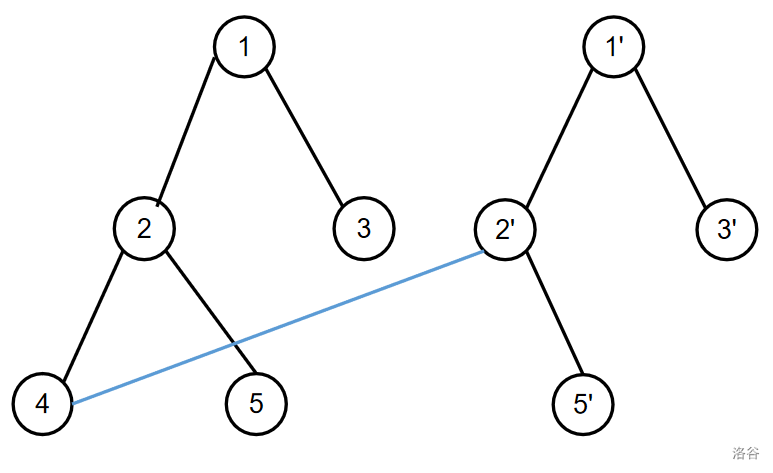
这是题目所给的样例,结合上述分析,我们断定题目描述的过程的本质是将原图部分被标记点对称到另一个 \(G\) 上,并且将 \(G\) 中的点与原图对应点的未被标记的相邻节点连接从而得到一个新图的过程。
那么我们现在应当使用一些手段分析这个图。因为这个图是部分对称,另外有一部分是关联原图与生成的图,所以考虑分类。
现在我们定义黑边指的是两个端点都已经被复制的边的数量,红边指的是端点由一个已复制点和一个未复制点所连接的边(满足题目范围的图可能很大,有些边两个端点都未被复制,由于对答案无贡献,我们不做考虑)。如下图所示:
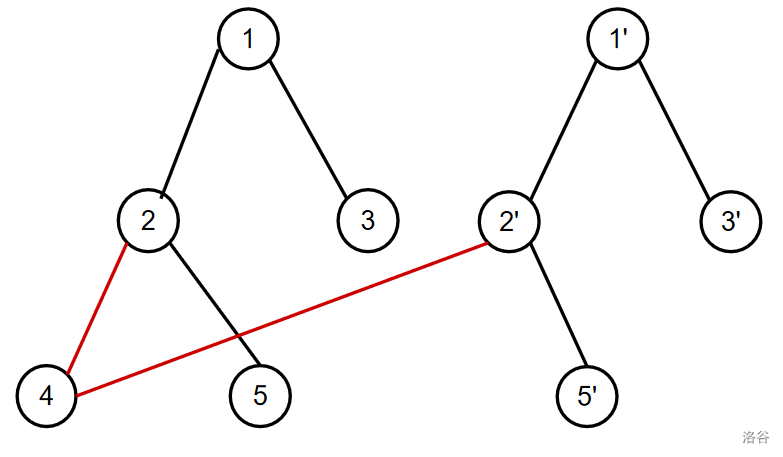
考虑生成树的问题,本质上是一个断边后导致断环成树的问题。所以考虑如何断边。似乎题目所给的样例有些弱,我们可以再制造一些更多点的样例。
先考虑删红边的问题,我们称两个红边为一对当且仅当他们有一个公共端点且另外两个端点是复制得到的。
现在给出一个引理:
证明:
考虑删去若干条黑边,使得原图和对称图中存在若干个极大联通子图,那么对于这些联通子图,若不存在一对红边连接原图与对称图,那么这些极大联通子图将对于整个图被彻底独立,所以至少存在一对这样的边。另一方面,如果存在两对,那么在原图上会形成一个环。所以最多只有一对。
有了这个引理,就可以换一个角度考虑计数的过程:
步骤一:
选择一些黑边作为断边,使得原图和对称图存在分别存在若干个联通块。
步骤二:
显然我们一定要使每个联通块存在一对红边,使得联通块与其对称部分有所相连。所以我们就钦定某一对红边不断,然后剩下的每一对红边选择其中一条进行断边。
发现整个过程与断边选择密切相关且有可计数性,考虑使用动态规划解决。注意到整个图的结构类似于两颗树以某种方式产生了对称联系从而产生了环,所以尝试使用树形dp方式定义状态。
2.构建模型:
因为图具有对称性,所以原图和对称图反过来是一样的效果,这意味着从一对分叉红边向两个图进行转移得到的结果是一样的,所以对于 \(u,u'\) 我们将其代表状态 \(f\) 存储在同一个dp值中(可以预见的是,最后的转移过程中应当是存在某种翻倍操作以满足对称性)。
定义:
表示对于 \(u,u'\) 所在联通块是(1)否(0)存在一对红边的方案数。显然这样定义的转移是符合树上联通块dp的模型的。转移考虑采用合并子树方法。需要注意的是,对于题目中每一次更新,我们都应当维护一个新产生的联通块进行dp,同时只遍历这个联通块以及其周边节点,因为周边节点以外的节点要么未被操作,要么在之前某一时刻被dp处理过了,所以不会对当前联通块造成贡献。
对于已存在一对红边的情况。若在前面的转移中已经保留了一对红边且子节点 \(v\) 所在联通块不存在与对称图的连接,那么应当保存连接 \((u/u',v/v')\) 所以直接把 \(T(v)\) 的贡献转移给 \(u\)。同理若在前面没有保留,那么必须使得 \(v\) 所在联通块有连接且直接贡献给 \(u\)。若 \(v\) 所在联通块已有连接,且前面转移也有连接,则我们必须断开 \(u\) 与 \(v\) 的连接,而经过上述分析我们得到无论断开黑边还是红边我们都应当将贡献翻倍,因为对于对称图和原图断边的贡献要分开算。
所以由上述分析可得:
而对于不存在红边的情况,分析方法是类似的,但是结果更简单:
由于是合并子树,所以在递归转移时应当注意先更新 \(f_{u,1}\) 然后再更新 \(f_{u,0}\)。
Code:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cstdio>
#define int long longconst int N = 5000 + 10, MOD = 998244353;
int n, f[N][2], head[N], cnt, fa[N];
bool vis[N];int find_fa(int x) {return x == fa[x] ? x : fa[x] = find_fa(fa[x]);
}
struct edge{int v, last;
}e[N << 1];void add(int u, int v) {e[++cnt].v = v;e[cnt].last = head[u];head[u] = cnt;
}void dfs(int u, int fath) {if (!vis[u]) return ;f[u][1] = 0;f[u][0] = 1;for (int i = head[u]; i; i = e[i].last) {int v = e[i].v;if (v == fath) continue;dfs(v, u);f[u][1] = (f[u][1] * f[v][0] % MOD + f[u][0] * f[v][1] % MOD + 2 * f[u][1] * f[v][1] % MOD) % MOD;f[u][0] = (f[u][0] * f[v][0] % MOD + 2 * f[u][0] * f[v][1] % MOD) % MOD;}
}signed main() {std::cin >> n;for (int i = 1; i <= n - 1; ++i) {int u, v;std::cin >> u >> v;add(u, v);add(v, u);}for (int i = 1; i <= n; ++i) {fa[i] = i;}for (int i = 1; i <= n; ++i) {f[i][0] = 0, f[i][1] = 1;}for (int i = 1; i <= n - 1; ++i) {int node;std::cin >> node;vis[node] = true;for (int i = head[node]; i; i = e[i].last) {int v = e[i].v;if (vis[v]) {fa[find_fa(v)] = node;}}dfs(node, -1);int ans = 1;for (int i = 1; i <= n; ++i) {if (fa[i] == i) ans = (ans * f[i][1]) % MOD;}std::cout << ans << '\n';}return 0;
}
