题目一:【模板】一维差分
https://ac.nowcoder.com/acm/problem/226303
解题思路
差分就是帮助我们解决"某一个区间统一加上(减去)某一个数"这类问题的。本题第一步先预处理出一个差分数组,假设差分数组的名字为f,f[i]就表示题给数组的当前元素与前一个元素的差值,即为a[i]-a[i-1]。第二步就是利用差分数组来解决区间统一加k的操作,这里有一个性质,如果我们要对[l,r]区间里边的每一个数都加上一个数,其实仅需要将f[l] += k,对f[r + 1] -= k,就可以了,请看下图的推导。

经过对f数组的操作,其实就实现了区间加k的操作,但是这仅仅是对f数组进行了操作,意思就是我对a数组的[l,r]区间进行了统一+k操作之后对f数组的改变我已经完成了,但题目要的是a数组区间+k之后的结果,所以第三步就是还原出a数组,其实只要对f数组执行前缀和操作就可以了,看下图。

代码实现
#include
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL a[N];
//注意:这里的f数组也可以直接利用差分数组的定义来实现(此时就不需要原始数组a了)
//在最一开始的时候可以理解为f数组里边的元素全都是0,而a数组也全都是0
//当读入a[i]的时候,就相当于对区间[i,i]执行了+a[i]的操作,所以可以直接利用差分数组的性质来创建差分数组
//即为 f[i] += a[i] f[i + 1] -= a[i];
LL f[N];//差分数组
int n, m;
int main()
{
cin >> n >> m;
for (int i = 1; i > a[i];
f[i] = a[i] - a[i - 1];
}
while (m--)
{
int l, r, k;
cin >> l >> r >> k;
f[l] += k;
f[r + 1] -= k;
}
//还原数组a
for (int i = 1; i <= n; i++)
{
a[i] = a[i - 1] + f[i];
cout << a[i] << " ";
}
return 0;
}注意事项:差分数组在使用的时候必须要所有操作全部操作完成之后才能还原出操作之后的数组,其实就是前缀和数组。有些题目会多次输入输出,此时如果用差分来做就会导致时间复杂度过高。
题目二:海底高铁
https://www.luogu.com.cn/problem/P3406
解题思路
题目的意思就是总共N个城市,Uim要去M个地方,需要我们输出最少花费,那么我们根据题意,每经过相邻的两个城市可能的花费就是要么直接花A元买车票,要么就是先用C元买一张IC卡,然后再用B元买车票,总计C+B元。我们可以将Uim要去的所有城市都看成一小段(就是每两个城市之间看成一段),计算出每一段他经过的次数,假设为k,要求的是最小的花费,仅需要min(Ak,C+Bk),这样就得到了该段的最小花费,最后将所有段的最小花费累加起来就是结果。
如何计算经过i段的次数呢?每次乘车,都可以看作是区间 [l,r] 里边的每一个元素+1,这就可以直接用差分来计算了(相当于模板题里边的修改差分数组),请看下图(图片中的f数组就是差分数组)。

代码实现
#include
using namespace std;
typedef long long LL;
const int N = 1E5 + 10;
LL f[N];//本题采用直接计算差分数组的方式
int n, m;
int main()
{
cin >> n >> m;
int l;
cin >> l;//标记区间左边的元素
for(int i = 2;i > r;
//第一个if就表示区间大小有问题,不能用swap,因为用了swap就找不到 l 了,直接反过来计算就可以了。
if (l > r)
{
f[r]++;
f[l]--;
}
else
{
f[l]++;
f[r]--;
}
l = r;//更新区间新的左值
}
//还原数组(数组里边的值就表示每段经过的次数)---前缀和
for (int i = 1; i > a >> b >> c;
ret += min(a * f[i], c + b * f[i]);
}
cout << ret << endl;
return 0;
}题目三:二维差分
https://ac.nowcoder.com/acm/problem/226337
解题思路
在解决这道题目之前,我们先来探究一下二维差分数组的性质。请看下图。
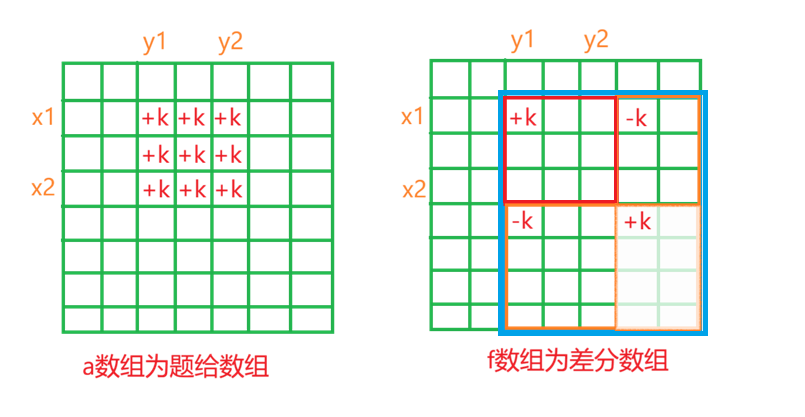
我们要知道,差分数组通过前缀和运算是可以还原出子矩阵统一+k之后的结果矩阵的。
现对[x1,y1]~[x2,y2]的a数组部分统一执行+k操作。(如上图所示)
假设我们在f数组[x1,y1]坐标位置处+k,就会导致以[x1,y1]为左上角的所有元素的前缀和都+k(即蓝色框出的部分)对于红色方框内的部分来说,前缀和+k的结果正是我们想要的,但是对于在蓝色方框内但不在红色方框内的部分,我们不需要它们+k,因此,需要对[x1,y2+1]和[x2+1,y1]这两个坐标内的元素执行-k操作,这样就可以让以它们为左上角的矩阵里边的所有元素不发生改变(即黄色框出部分),但是阴影部分的元素很显然在计算前缀和的时候多减了一个k,所以我们还需要在[x2+1,y2+1]的地方+k。
知道了二维差分数组的性质之后,对于本道题,第一步先预处理出一个差分数组,每读入一个元素,就相当于是在a数组的[i,j]~[i,j]区间位置实现了一个+k的效果,那么根据二维差分数组的性质,我们就可以直接预处理出一个差分数组。接着就可以执行m次操作了,还是利用二维差分的性质。最后就是利用前缀和还原出区间+k之后的数组。
代码实现
#include
using namespace std;
typedef long long LL;
const int N = 1010;
LL f[N][N];
int n, m, q;
int main()
{
cin >> n >> m >> q;
//预处理差分数组----下边也可以将二维差分的性质封装成一个函数
for (int i = 1; i > x;
f[i][j] += x;
f[i][j + 1] -= x;
f[i + 1][j] -= x;
f[i + 1][j + 1] += x;
}
}
//q次操作
while (q--)
{
int x1, y1, x2, y2, k;
cin >> x1 >> y1 >> x2 >> y2 >> k;
f[x1][y1] += k;
f[x1][y2 + 1] -= k;
f[x2 + 1][y1] -= k;
f[x2 + 1][y2 + 1] += k;
}
//前缀和操作
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + f[i][j];
cout << f[i][j] << " ";
}
cout << endl;
}
return 0;
}题目四:地毯
https://www.luogu.com.cn/problem/P3397
解题思路
本题基本上就是套用上边的那道模板题目,一共是有m块地毯,每给出一块地毯的坐标就相当于在[x1,y1]~[x2,y2]范围之内所有的值+1,最后利用前缀和还原出”+k“之后的结果数组就可以了。
代码实现
#include
using namespace std;
const int N = 1010;
int f[N][N];
int n, m;
int main()
{
cin >> n >> m;
while (m--)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
f[x1][y1] += 1;
f[x1][y2 + 1] -= 1;
f[x2 + 1][y1] -= 1;
f[x2 + 1][y2 + 1] += 1;
}
//前置和还原
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + f[i][j];
cout << f[i][j] << " ";
}
cout << endl;
}
return 0;
}