《电路基础》第四章学习笔记
本章内容:
认识什么是线性电路,学习戴维南定理和诺顿定理。
-
线性性质
-
线性是齐次性与可加性的组合
-
齐次性:如果输入乘以一个常数,那么输出也会相应乘以同一个常数。
例如这个公式:
\[v=iR \]如果电流乘以常数k,那么电压也相应地增加了 k 倍。
\[kiR=kv \] -
可加性:对各个输入之和的响应等于每个输入单独作用于系统时的响应之和,仍以上述电阻的电压-电流关系为例。
我们列出两个式子:
\[v_{1}=i_{1}R \]\[v_{2}=i_{2}R \]两个式子相加,得到:
\[v=(i_{1}+i_{2})R=i_{1}R+i_{2}R=v_{1}+v_{2} \]
-
-
线性电路是指输入与输出呈线性关系的电路
-
-
叠加原理
-
内容:
线性电路中元件的两端电压(或流经元件的电流)是在每个独立源单独作用下在该元件两端的电压的代数和。
-
步骤:
- 关闭除一个独立电源以外其他所有独立电源,求出有效独立源作用于电路的输出(电压或电流)
- 对于其他各独立源重复上面的步骤
- 将各个独立源单独作用于电路时产生的响应进行代数相加,从而得到电路总的响应。
-
优缺点:
- 优点:降低电路的复杂程度,将复杂电路简化
- 缺点:涉及的计算比较多
-
适用性:
- 叠加原理的基础是线性性质,因此它并不适用于各电源产生的功率,因为电阻吸收的功率遂电压或电流的平方关系变化。
-
-
电源变换
-
电源变换是指用与电阻并联的电流源 \(i_{5}\) 取代与电阻串联的电压源 \(v_{5}\) (或者反之)的转换过程
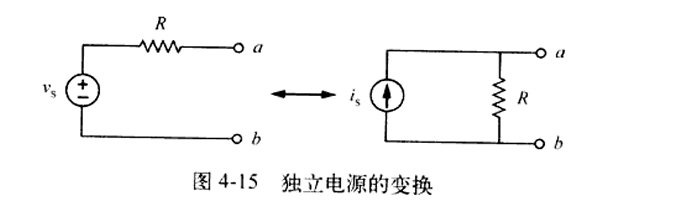
电源变换同样适用于受控源,但前提是必须对受控电量做细致的处理。
实则等效电路法,高中学过,不赘述了。
-
-
戴维南定理
-
内容:
用等效电路取代电路中不变部分。
戴维南等效电路:
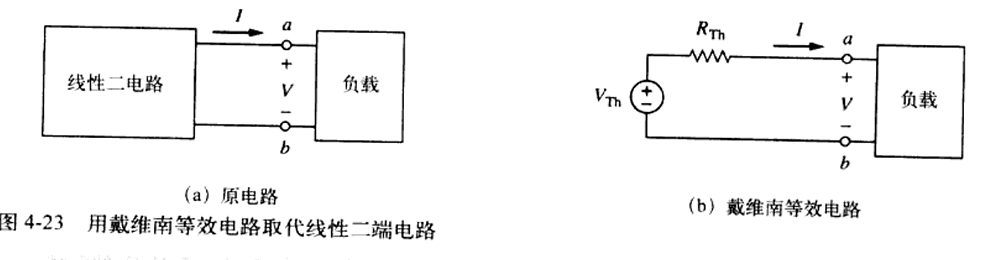
线性二端电路可以用一个由电压源 \(V_{Th}\) 和与之串联的电阻 \(R_{Th}\) 组成的等效电路所取代、其中 \(V_{Th}\) 为端口的开路电压,\(R_{Th}\) 为独立源关闭时端口的输入(或者等效)电阻
-
两种特殊情况:
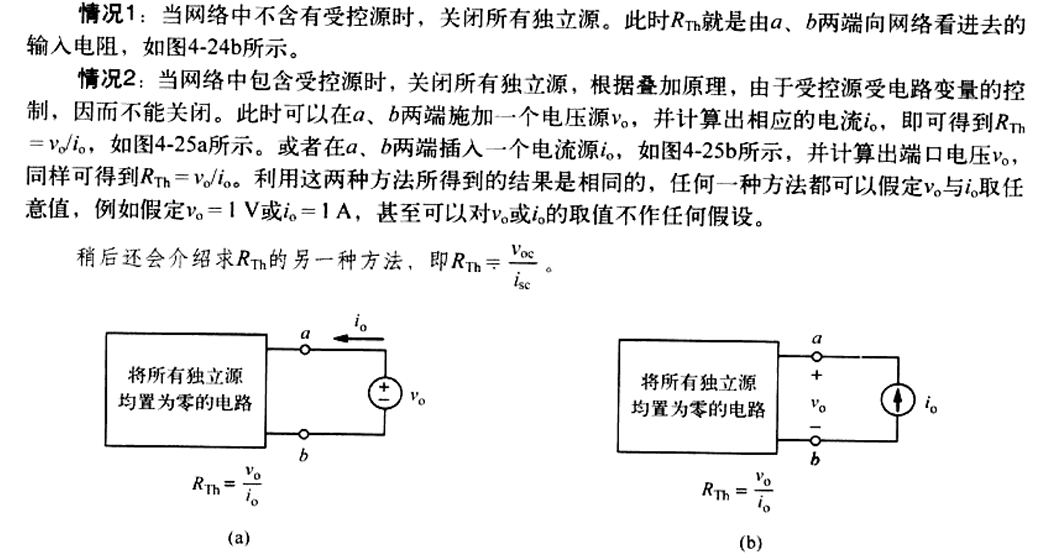
-
-
诺顿定理
-
内容:
线性二端电路可以用由电流源 \(I_{N}\) 和与之并联的电阻 \(R_{N}\)构成的等效电路所取代,其中 \(I_{N}\) 为流过端口的短路电流。\(R_{N}\) 为独立源关闭时,端口的输入电阻或等效电阻。
(这句话有病句啊qwq,到底什么意思?而且是书上的原话)
等效电路:

由电源变换的关系可知,戴维南等效电阻与诺顿等效电阻是相等的。
-
-
最大功率传递定理
-

传递给负载的功率为:
\[p=i^{2}R_{L}=(\frac{V_{Th}}{R_{Th}+R_{L}} )^{2}R_{L} \]
-
