当前位置：首页 > news >正文

牛客刷题-Day11

news 2025/10/11 9:30:09

牛客刷题-Day11

今日刷题：\(1051-1055\)

1051 [HAOI2012]音量调节

题目描述

一个吉他手准备参加一场演出。他不喜欢在演出时始终使用同一个音量，所以他决定每一首歌之前他都要改变一次音量。在演出开始之前，他已经做好了一个列表，里面写着在每首歌开始之前他想要改变的音量是多少。每一次改变音量，他可以选择调高也可以调低。
音量用一个整数描述。输入文件中给定整数 \(beginLevel\)，代表吉他刚开始的音量，以及整数 \(maxLevel\)，代表吉他的最大音量。音量不能小于 \(0\) 也不能大于 \(maxLevel\)。输入文件中还给定了 \(n\) 个整数 \(c_1,c_2,c_3,...,c_n\)，表示在第 \(i\) 首歌开始之前吉他手想要改变的音量是多少。
吉他手想以最大的音量演奏最后一首歌，你的任务是找到这个最大音量是多少。

输入描述

第一行依次为三个整数：\(n\)，\(beginLevel\)，\(maxlevel\)。
第二行依次为 \(n\) 个整数：\(c_1,c_2,c_3,...,c_n\)。

输出描述

输出演奏最后一首歌的最大音量。如果吉他手无法避免音量低于 \(0\) 或者高于 \(maxLevel\)，输出 \(-1\)。

示例

输入

3 5 10
5 3 7

输出

备注

\(1≤n≤50\)，\(1≤c_i≤maxLevel\)，\(1≤maxLevel≤1000\)，\(0≤beginLevel≤maxLevel\)。

解题思路

状态表示：\(f_{i,j}\) 表示唱第 \(i\) 首歌是否可以达到 \(j\) 音量；
状态计算：从 \(i-1\) 到 \(i\)，要么调高，要么调低音量，\(f_{i,j-c_i} = f_{i,j-c_i} | f_{i-1,j}\)，\(f_{i,j+c_i} = f_{i,j+c_i} | f_{i-1,j}\)，注意边界。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 60, M = 1010;int n, st, ed;
int c[N], f[N][M]; // f[i][j] 表示唱第 i 首歌是否可以达到 j 音量int main() {scanf("%d%d%d", &n, &st, &ed);for (int i = 1; i <= n; i++)scanf("%d", &c[i]);f[0][st] = 1;for (int i = 1; i <= n; i++)for (int j = ed; j >= 0; j--) {if (j - c[i] >= 0)f[i][j - c[i]] = f[i][j - c[i]] | f[i - 1][j];if (j + c[i] <= ed)f[i][j + c[i]] = f[i][j + c[i]] | f[i - 1][j];}int ans = -1;for (int i = 0; i <= ed; i++)if (f[n][i])ans = i;printf("%d\n", ans);return 0;
}

1052 [NOIP2014]飞扬的小鸟

题目描述

为了简化问题，我们对游戏规则进行了简化和改编：

游戏界面是一个长为 \(n\)，高为 \(m\) 的二维平面，其中有 \(k\) 个管道（忽略管道的宽度）。
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。
小鸟每个单位时间沿横坐标方向右移的距离为 \(1\)，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度 \(X\)，每个单位时间可以点击多次，效果叠加；如果不点击屏幕，小鸟就会下降一定高度 \(Y\)。小鸟位于横坐标方向不同位置时，上升的高度 \(X\) 和下降的高度 \(Y\) 可能互不相同。
小鸟高度等于 \(0\) 或者小鸟碰到管道时，游戏失败。小鸟高度为 \(m\) 时，无法再上升。
现在，请你判断是否可以完成游戏。如果可以，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

输入描述

第 \(1\) 行有 \(3\) 个整数 \(n\)，\(m\)，\(k\)，分别表示游戏界面的长度，高度和水管的数量，每两个整数之间用一个空格隔开；
接下来的 \(n\) 行，每行 \(2\) 个用一个空格隔开的整数 \(X\) 和 \(Y\)，依次表示在横坐标位置 \([0,n-1]\) 上玩家点击屏幕后，小鸟在下一位置上升的高度 \(X\)，以及在这个位置上玩家不点击屏幕时，小鸟在下一位置下降的高度 \(Y\)。
接下来 \(k\) 行，每行 \(3\) 个整数 \(P\)，\(L\)，\(H\)，每两个整数之间用一个空格隔开。每行表示一个管道，其中 \(P\) 表示管道的横坐标，\(L\) 表示此管道缝隙的下边沿高度为 \(L\)，\(H\) 表示管道缝隙上边沿的高度（输入数据保证 \(P\) 各不相同，但不保证按照大小顺序给出）。

输出描述

第一行，包含一个整数，如果可以成功完成游戏，则输出 \(1\)，否则输出 \(0\)。
第二行，包含一个整数，如果第一行为 \(1\)，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

示例1

输入

输出

1
6

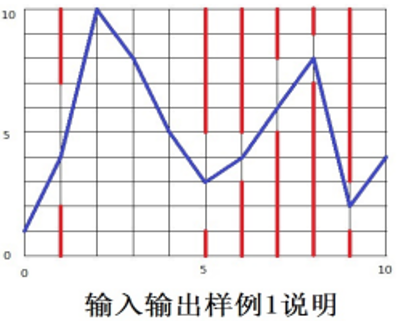
说明
如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

示例2

输入

输出

0
3

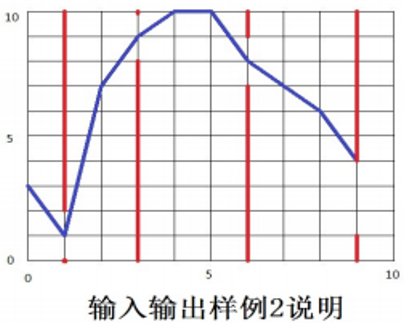
说明
如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

备注

对于 \(30\%\) 的数据：\(5≤n≤10,5≤m≤10,k=0\)，保证存在一组最优解使得同一单位时间最多点击屏幕 \(3\) 次；
对于 \(50\%\) 的数据：\(5≤n≤20,5≤m≤10\)，保证存在一组最优解使得同一单位时间最多点击屏幕 \(3\) 次；
对于 \(70\%\) 的数据：\(5≤n≤1000,5≤m≤100\)；
对于 \(100\%\) 的数据：\(5≤n≤10000,5≤m≤1000,0≤k\)。

解题思路

状态表示：\(f_{i,j}\) 表示在 i 处高度为 j 的点击次数。
状态计算：初始在横坐标为 \(0\) 且任意高度都可以，因此 \(f_{0,j}=0,0\le j\le m\)；如果是点击上升，因为可以多次点击，则 \(f_{i,j}=min\{f_{i-1,j-x_{i-1}}+1,f_{i-1,j-2 * x_{i-1}}+2,...\}\)；如果下降，则 \(f_{i,j}=max\{f_{i,j},f_{i-1,j+y_{i-1}}\}\)；更新完之后，如果对应的点存在管道，则修改为正无穷，表示该处不可达。
优化：在点击上升的转移方程中，如果枚举点击次数，则会多套一层循环，时间复杂度不允许；类似完全背包的优化思路，\(f_{i,j}=min\{f_{i-1,j-x_{i-1}}+1,f_{i-1,j-2 * x_{i-1}}+2,...\}\)，\(f_{i,j-x_{i-1}}=min\{f_{i-1,j-2*x_{i-1}}+1,f_{i-1,j-3*x_{i-1}}+2,...\}\)，后一个式子替换前面的得到 \(f_{i,j}=min\{f_{i-1,j-x_{i-1}}+1,f_{i,j-x_{i-1}}+1\}\)。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = 1010 * 2;int n, m, k;
struct Pipe {int l, h;
} g[N]; // 管道
int x[N], y[N];
int f[N][M]; // 在 i 处高度为 j 的点击次数
bool pos[N];int main() {scanf("%d%d%d", &n, &m, &k);for (int i = 0; i < n; i++)scanf("%d%d", &x[i], &y[i]);for (int i = 0; i < k; i++) {int p;scanf("%d", &p);pos[p] = true;scanf("%d%d", &g[p].l, &g[p].h);}memset(f, 0x3f, sizeof f);for (int i = 0; i <= m; i++)f[0][i] = 0;for (int i = 1; i <= n; i++) {for (int j = x[i - 1] + 1; j <= x[i - 1] + m; j++)f[i][j] = min(f[i - 1][j - x[i - 1]] + 1, f[i][j - x[i - 1]] + 1);for (int j = m + 1; j <= m + x[i - 1]; j++)f[i][m] = min(f[i][m], f[i][j]);for (int j = 1; j <= m - y[i - 1]; j++)f[i][j] = min(f[i][j], f[i - 1][j + y[i - 1]]);if (pos[i]) {for (int j = 1; j <= g[i].l; j++)f[i][j] = 0x3f3f3f3f;for (int j = g[i].h; j <= m; j++)f[i][j] = 0x3f3f3f3f;}}int ans = 0x3f3f3f3f;for (int i = 1; i <= m; i++)ans = min(ans, f[n][i]);if (ans != 0x3f3f3f3f) {printf("1\n%d", ans);} else {int i = 0, j = 0;for (i = n; i; i--) {for (j = 1; j <= m; j++)if (f[i][j] < 0x3f3f3f3f)break;if (j <= m)break;}int cnt = 0;for (j = 1; j <= i; j++)if (pos[j])cnt++;printf("0\n%d", cnt);}return 0;
}

1054 [USACO 2008 Jan S]Running

题目描述

The cows are trying to become better athletes, so Bessie is running on a track for exactly \(N\) (\(1 ≤ N ≤ 10,000\)) minutes. During each minute, she can choose to either run or rest for the whole minute.
The ultimate distance Bessie runs, though, depends on her 'exhaustion factor', which starts at \(0\). When she chooses to run in minute \(i\), she will run exactly a distance of \(D_i\) (\(1 ≤ D_i ≤ 1,000\)) and her exhaustion factor will increase by \(1\) -- but must never be allowed to exceed \(M\) (\(1 ≤ M ≤ 500\)). If she chooses to rest, her exhaustion factor will decrease by \(1\) for each minute she rests. She cannot commence running again until her exhaustion factor reaches \(0\). At that point, she can choose to run or rest.
At the end of the N minute workout, Bessie's exaustion factor must be exactly \(0\), or she will not have enough energy left for the rest of the day.
Find the maximal distance Bessie can run.

输入描述

Line \(1\): Two space-separated integers: \(N\) and \(M\);
Lines \(2..N+1\): Line \(i+1\) contains the single integer: \(D_i\).

输出描述

Line \(1\): A single integer representing the largest distance Bessie can run while satisfying the conditions.

示例

输入

输出

说明
Bessie runs during the first minute (distance=\(5\)), rests during the second minute, runs for the third (distance=\(4\)), and rests for the fourth and fifth. Note that Bessie cannot run on the fifth minute because she would not end with a rest factor of \(0\).

解题思路

状态表示：\(f_{i,j}\) 表示第 \(i\) 分钟疲劳值为 \(j\) 时的运动距离，求解最大值。
状态计算：如果继续运动，则 \(f_{i,j}=max\{f_{i,j},f_{i-1,j-1}+d_i\}\)；如果选择休息，则疲劳值为 \(0\) 也可以继续休息，\(f_{i,0}=max\{f_{i,0},f_{i-1,0}\}\)，要么就只能休息至疲劳值归零，\(f_{i,0}=max\{f_{i,0},f_{i-j,j}\}\)，此时休息时间和疲劳值在数值上相等。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = 510;int n, m;
int d[N];
int f[N][M];int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++)scanf("%d", &d[i]);memset(f, -0x3f, sizeof f);f[0][0] = 0;for (int i = 1; i <= n; i++) {for (int j = 0; j <= min(i, m); j++)f[i][0] = max(f[i][0], f[i - j][j]);f[i][0] = max(f[i][0], f[i - 1][0]);for (int j = 1; j <= m; j++)f[i][j] = max(f[i][j], f[i - 1][j - 1] + d[i]);}printf("%d\n", f[n][0]);return 0;
}

1055 金币馅饼

题目描述

最近，奶牛们热衷于把金币包在面粉里，然后把它们烤成馅饼。第 \(i\) 块馅饼中含有 \(N_i(1<=N_i<=25)\) 块金币，并且，这个数字被醒目地标记在馅饼表面。
奶牛们把所有烤好的馅饼在草地上排成了一个 \(R\) 行 \((1<=R<=100)\) \(C\) 列 \((1<=C<=100)\) 的矩阵。你现在站在坐标为 \((1,1)\) 的馅饼边上，当然，你可以拿到那块馅饼里的所有金币。你必须从现在的位置，走到草地的另一边，在坐标为 \((R,C)\) 的馅饼旁边停止走动。每做一次移动，你必须走到下一列的某块馅饼旁边，并且，行数的变动不能超过1（也就是说，如果现在你站在坐标为 \((r,c)\) 的馅饼边上，下一步你可以走到坐标为 \((r-1,c+1)\)，\((r,c+1)\)，或者 \((r+1,c+1)\) 的馅饼旁边）。当你从一块馅饼边经过，你就可以拿走馅饼里所有的金币。当然啦，你一定不会愿意因半路离开草地而失去唾手可得的金币，但，最终你一定得停在坐标为 \((R,C)\) 的馅饼旁边。
现在，你拿到了一张标记着馅饼矩阵中，每一块馅饼含金币数量的表格。那么，按照规则，你最多可以拿到多少金币呢？

输入描述

第 \(1\) 行：两个用空格隔开的整数，\(R\) 和 \(C\)；
第 \(2..R+1\) 行：每行包含 \(C\) 个用空格隔开的正整数，依次表示一行中从左往右各个馅饼里金币的数量。

输出描述

第 \(1\) 行: 输出一个正整数，表示你所能收集到的最大金币数目。

示例

输入

3 7
6 5 3 7 9 2 7
2 4 3 5 6 8 6
4 9 9 9 1 5 8

输出

解题思路

状态表示：\(f_{i,j}\) 表示到达 \(i\) 行 \(j\) 点的金币数，求解最大值；
状态计算：\(f_{i,j}=max\{f_{i,j},max\{f_{i-1,j-1},f_{i,j-1},f_{i+1,j-1}+g_{i,j}\}\}\)，这里可以看出是根据前一列修改后一列状态，因此遍历时需要先从列开始。

C++ 代码

#include <bits/stdc++.h>
using namespace std;
const int N = 110;int n, m;
int g[N][N], f[N][N];int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)scanf("%d", &g[i][j]);memset(f, -0x3f, sizeof f);f[1][1] = g[1][1];for (int j = 2; j <= m; j++)for (int i = 1; i <= n; i++) {f[i][j] = max(f[i][j], f[i][j - 1] + g[i][j]);if (i - 1 >= 1)f[i][j] = max(f[i][j], f[i - 1][j - 1] + g[i][j]);if (i + 1 <= n)f[i][j] = max(f[i][j], f[i + 1][j - 1] + g[i][j]);}printf("%d\n", f[n][m]);return 0;
}

查看全文

http://www.hskmm.com/?act=detail&tid=28429