1. 论文介绍
论文题目:Prompt Engineering Through the Lens of Optimal Control
论文领域:AI Agent,提示词工程PE
论文发表:Journal of Machine Learning, 2, 241-258, 2023
论文背景:首次为提示词工程的研究提供了数学理论框架,并进一步强调在与AI互动过程中“多轮对话”的重要性。

2. 论文摘要
提示工程(PE)已经成为指导大型语言模型(LLM)解决复杂任务的关键技术。它的重要性是突出的潜力,显着提高人机交互的效率和有效性。随着任务变得越来越复杂,最近的高级PE方法已经超越了单轮交互的局限性,将多轮交互纳入其中,从而允许与LLM进行更深入、更细致的接触。在本文中,我们提出了一个适合与LLM进行多轮交互的最优控制框架。该框架提供了一个统一的数学结构,不仅使现有的PE方法系统化,而且为严格的分析改进奠定了基础。此外,我们通过集成方法和多智能体协作将该框架扩展到PE,从而扩大了适用范围。通过采用最优控制的观点,我们提供了对现有PE方法的新见解,并强调了值得未来研究的理论挑战。此外,我们的工作为开发更有效、更具解释性的PE方法奠定了基础。
3. 相关介绍
3.1 提示词工程PE
提示词工程(PE)在2020年首次出现在LLM领域,精心设计的提示词可以显著提高LLM的能力而不需额外的模型训练。
PE的发展可以在自然语言编程的更大范围内进行情景化,就像从机器语言向C语言等高级语言的过渡。
提示词是与LLM交互的起点,可以是用自然语言给出的问题,陈述或命令。本文主要关注与LLM的多轮交互。
多轮交互的重要性是可以从LLM中获得高质量响应。正如问诊医师那样,只有在多轮的对话询问下才能够保证就诊的结果正确率最高。
3.2 本文贡献
1,文章核心是提出了一种适用于LLM的多轮交互的最优控制框架。将现有的各种方法统一在一个单一的数学框架下,为分析和改进快速设计提供了严格的基础。
2,我们强调了框架揭示的理论挑战,特别是关于多轮交互的形式化和优化。虽然复杂,这些问题提供了令人兴奋的方向,为今后的研究,以加深数学理解体育。
3,我们的观点对当前技术的固有能力和局限性产生了有价值的见解。这些可以催化体育创新,推动人机交互的边界。
4,将该框架扩展到集成PE方法和多agent PE,成为研究LLM复杂相互作用的重要垫脚石。
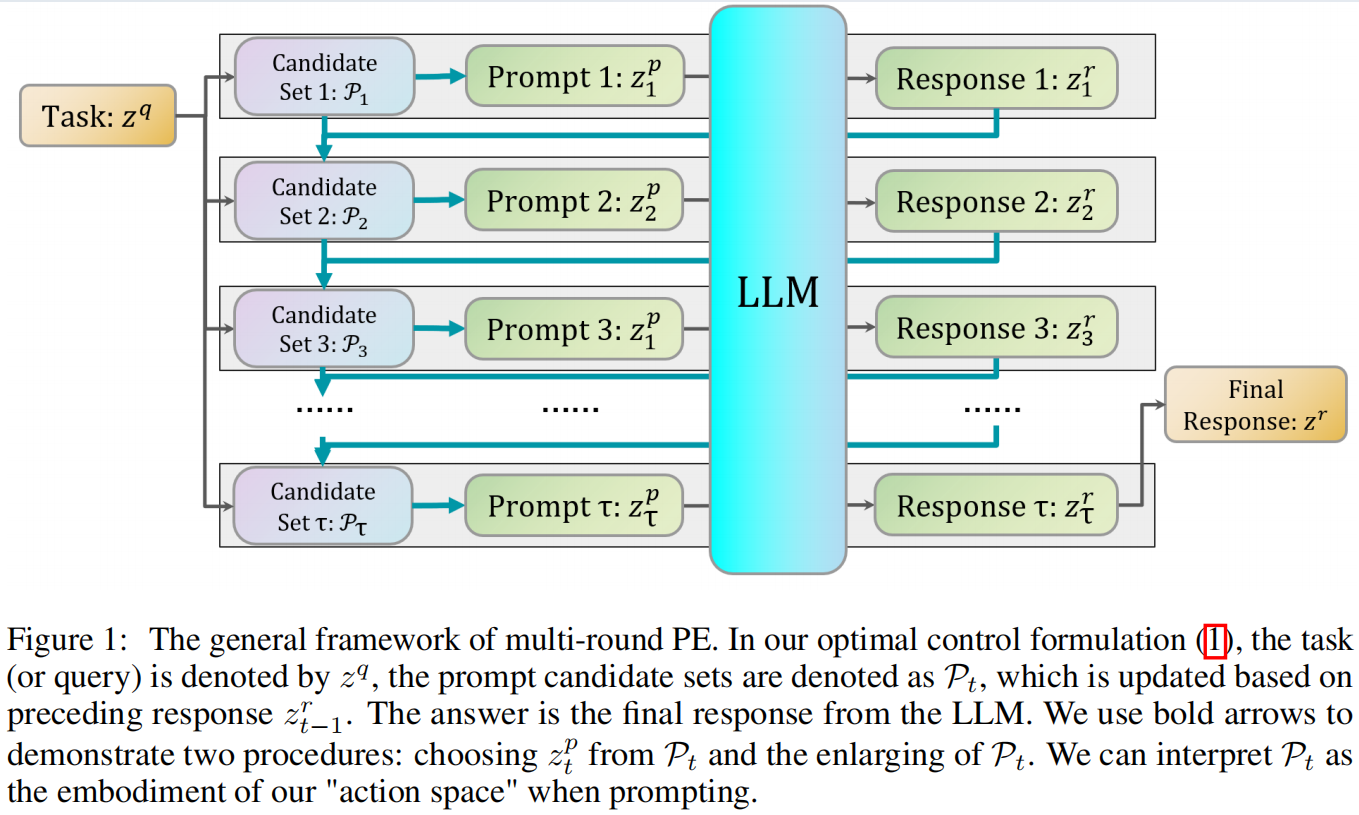
4. 总框架
把文本空间定义为Z,Z空间中的元素是从标记词汇表中选择的一些标记的组合 𝒯。
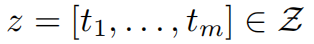
其中t属于 𝒯。那么对于LLM的作用是把提示词文本映射为回答词文本
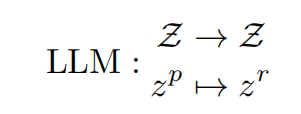
其中$z^p$ 代表是提示词,$z^r$代表的是回答文本。其中LLM并不是确定性变化,而是基于随机环境中的运行。文本生成中随机采样导致的固有可变性,可以为同一输入提示词产生不同的输出。
可以把该问题转为最优化问题,给定一个任务,目标是获取最优响应,最优性是使用了评估函数f来测量
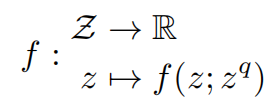
PE的目的是找到一系列导致最佳响应的提示词
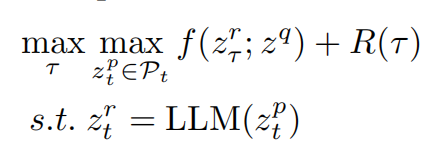
其中R(t)是一个正则化项,强制限制了执行的最大交互次数
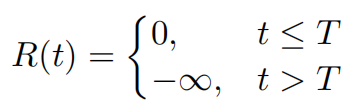
在公式中, ${𝒫_t}_{t=1}^τ$ 是一系列在的轮次中扩展的提示词候选集合,满足
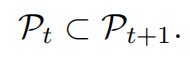
总结下来,整个框架上来看,PE本质上是优化问题的制定和解决,包含以下步骤
- 确定合适的评估函数f
- 为提示词候选集$p_t$ 建立更新的规则
- 求解由此产生的最优控制问题,即在$p_t$ 中选择 $z_t^P$
三个步骤迭代最终求得最优的结果。前两步跟问题表述有关,最后一步则侧重于解决潜在问题。
![pettloc08]()
提示词工程的潜力和挑战
潜力方面
LLM可以实现有效PE的关键在于巨大的知识能力和固有的可变性。在每一轮交互中,LLM可以被视为从定义的概率分布中抽取样本,该分布以Z先前的提示和响应为条件。PE的目标是让LLM促进一系列样本,以接近用户目标知识的真实分布。
基于这个理想化假设,在PE背景下开发LLM提供了一个明确的目标:完善其抽样过程,以通过迭代提示更好地近似所需要的知识分布。
挑战方面
对PE的问题表述,复杂性源自语言集Z的离散型和结构化性质。设计基于规则的语言集合上本质上具有挑战性。提示词候选集随着时间t变化而分析潜在的最优控制问题时增加了另一层复杂性。
另一方面在优化提示词过程中,需要使用无梯度技术,如随机搜索,强化学习。
总的来说,提示词的质量影响着LLM的表现,哪些因素限制了提示词的质量是一个重要的研究问题。
5. 提示词工程方法
PE包含三个关键因素,评估函数f,提示词候选集$p_t$,解决最优控制问题的方法。因为评估函数因为不同的任务而有很大区别。本节主要讨论放大机制$p_t$ 和解决随之而来的最优控制问题
扩散提示词候选集
通过前轮的回复来放大
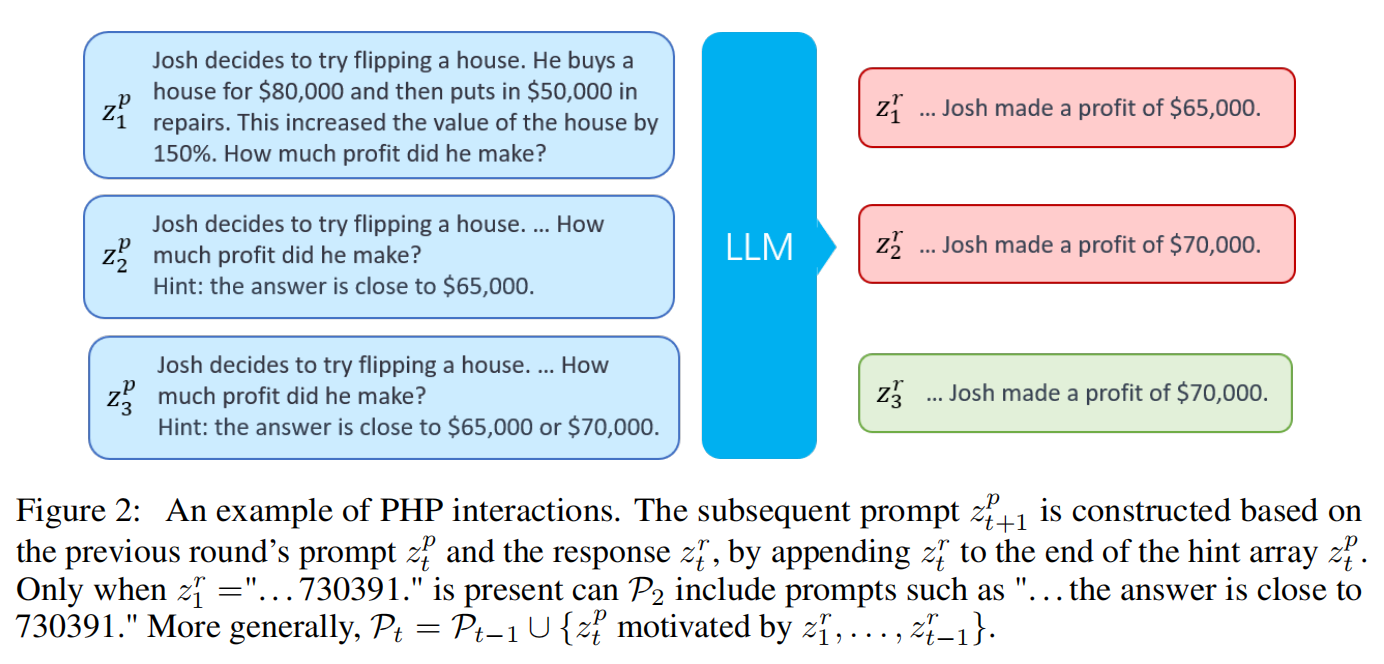
多轮PE的一个分支是通过采用以前的响应作为后面提示的一部分来扩大其提示候选集。以渐进式暗示提示词PHP(Progressive-Hint Prompting)为例。
PHP专注于算术任务,在 PHP 中,LLM 的先前输出用于构造后续输入。可以表达为
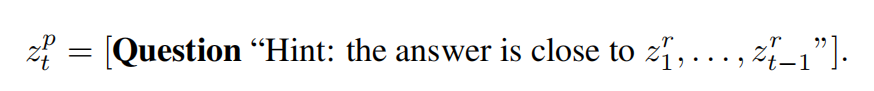
PHP停止的标准是正确答案在提示词中存在,该规则依赖于启发式概念。
通过直接提示词来放大
这种方法通过提示词来主动扩充提示词候选集,包括指导LLM分解初始任务,从LLM获取背景信息。 这种方法有效增强了提示词候选集合。以LtM(Least To Most)方法为例
LtM主要面对推理任务,采用“描述问题”的方式,可表达为
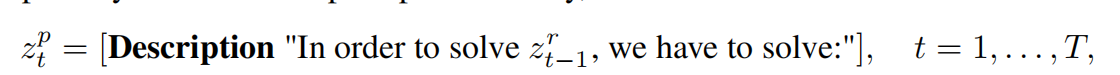
问题可以被描述为
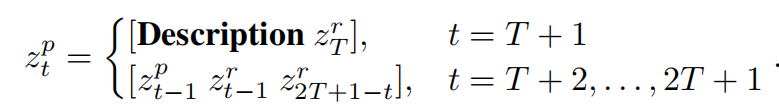
示意框架图为
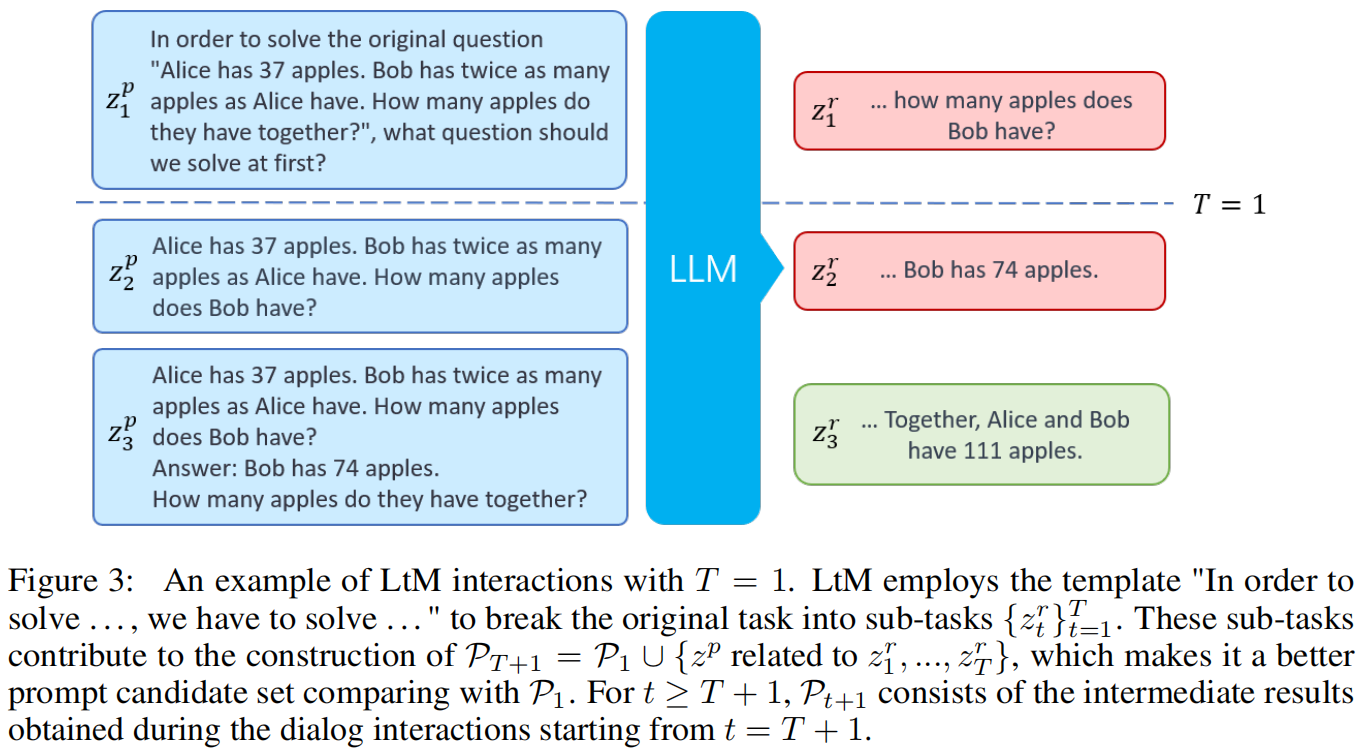
提示词优化
随机搜索
随机搜索方法随机生成提示词,并使用特定任务对其评估。选择自动提示词工程(APE)为例。APE 旨在在 LLM 可以提供的所有候选提示中找到最佳提示。
其他例子包括 Tree of Thought (ToT),它专门从事多轮PE。ToT采用树状搜索优化策略,通过迭代评估系统地探索提示序列。
强化学习方法
优化提示词的一个最重要的挑战在于底层语言空间 𝒵 的离散性质,它不适合假设连续空间的传统优化技术。RL算法在不了解底层模型的情况下运行,为优化 PE 中的控制问题提供了可行的策略。
APE 和 ToT 专注于一种相当具体的优化方法,缺乏通用策略,而 LtM 和 PHP 则扩展了特定任务的提示候选集,而没有更广泛的适用性。
通过实现整体的、基于数学的理解,我们的框架提供了将 PE 解决方案提升到新复杂水平的工具。我们看到了从独立方法转向具有更广泛适用性的综合技术的巨大潜力。
6. 进一步扩展
通过集成方法来提示工程
集成方法长期以来一直有助于提高预测准确性和鲁棒性。在多个查询中使用相同的提示,利用 LLM 固有的随机性来引入变化。特定的集成函数,表示为 En(⋅) ,进一步决定了集成 PE 方法的特征。
任务的最终响应 zr 是使用应用于所有这些响应的集成函数 En(⋅) 制定的
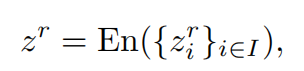
通过集成方法对 PE 的最优控制问题可以表述
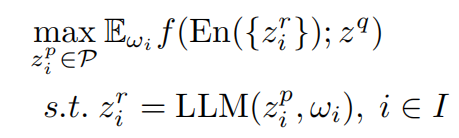
特定的集成函数,表示为 En(⋅) ,进一步决定了集成 PE 方法的特征。例如,当采用多数投票方案时 En(⋅) ,自洽 CoT的方法自然被封装。相反,当作为复杂性阈值实现时 En(⋅) ,就会出现复杂性 CoT
通过多代理协作进行提示工程
多智能体系统是指协作工作以实现集体目标的交互式智能体的集合。在这种情况下,“代理”被定义为在给定的初始指令下运行的LLM。不同的初始指令会产生不同的代理,这些代理在其行为和能力上可能表现出相当大的异质性。每个代理负责生成提示以促进彼此之间的交互。
我们将优化目标 f 扩展到 fi 评估每个相应代理的 PE 质量。
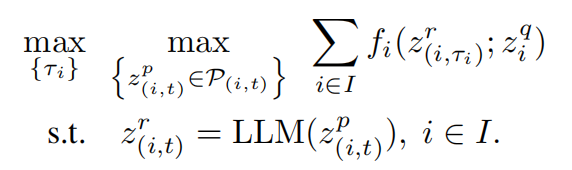
7. 总结
本文章针对提示词工程建立了一套分析和评估的数学模型,也奠定了其通往AI Agent的实用性和可用性。
8. 个人感悟
文章不会涉及太多的难的证明,总的来说归纳和提取抽象的能力很重要。