moectf2025-reverse-wp
upx
壳是什么?upx是什么?upx可以用来干什么?
用自己的upx脱壳
upx -d +文件地址
然后就去ida里面编译
但是找不到main函数
我们直接shift+F12查看字符串
然后点进去
鼠标移到这里
按X
然后定位到主函数
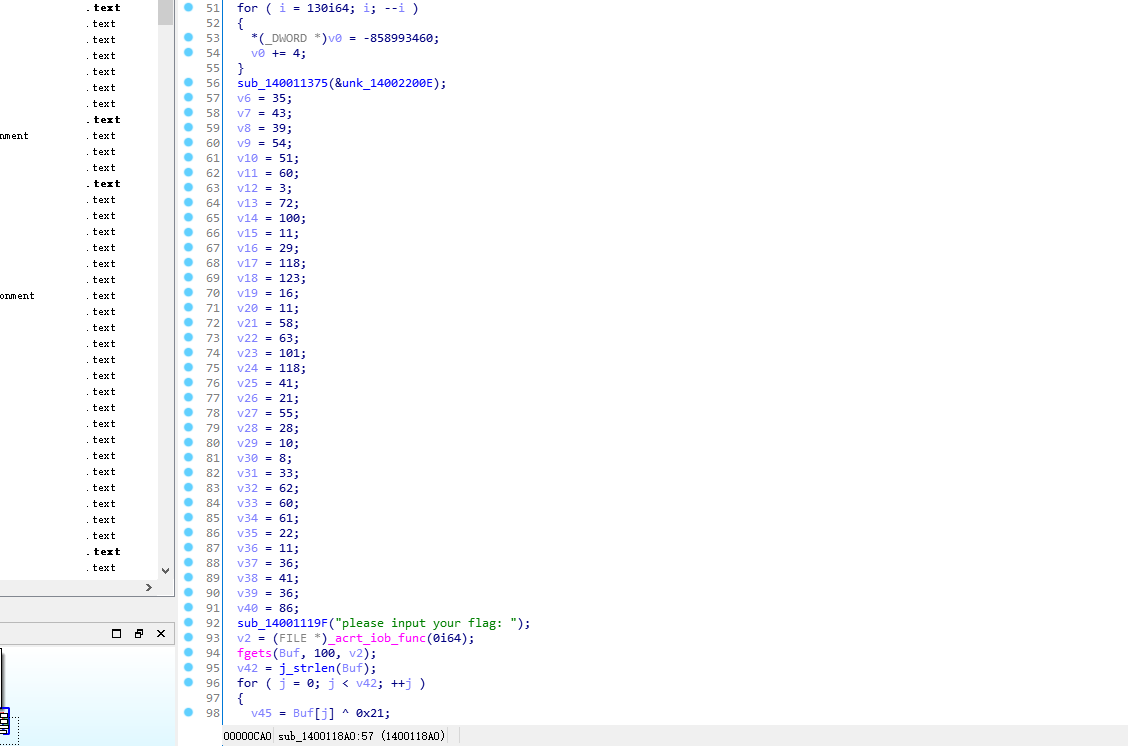
然后机分析里面的算法
#!/usr/bin/env python3
# 35-byte 目标序列
T = [35, 43, 39, 54, 51, 60, 3, 72,100, 11,29,118,123, 16, 11, 58, 63,101,118, 41,21, 55, 28, 10, 8, 33, 62, 60, 61, 22,11, 36, 41, 36, 86
]# 已知前缀 7 字节
prefix = b'moectf{'
flag = [0] * 35
flag[:7] = prefix# 从索引 7 开始向后递推
for i in range(7, 35):flag[i] = T[i-1] ^ (flag[i-1] ^ 0x21) & 0xFF# 合成最终 flag
print('moectf{' + bytes(flag[7:]).decode() + '}')
得到flag
ez3
Do you know z3 solver?
Z3在CTF逆向中有什么用?
我们在做CTF逆向题的时候,当我们已经逆向到最后求flag或者具体数值解的时候,例如最简单的:我们知道了未知量x,y,也知道了约束条件x+y=5,那么此时我们就可以使用Z3来求解x和y的值,因为x和y的值肯定有多个解,而我们最后的flag肯定只有一个,那么我们就可以继续添加约束条件来减少解的数量,最后得出正确的flag。
几个常用API
Solver():创建一个通用求解器,创建后我们可以添加我们的约束条件,进行下一步的求解。**
**
add():添加约束条件,通常在solver()命令之后,添加的约束条件通常是一个逻辑等式。
check():通常用来判断在添加完约束条件后,来检测解的情况,有解的时候会回显sat,无解的时候会回显unsat。**
**
model():在存在解的时候,该函数会将每个限制条件所对应的解集取交集,进而得出正解。
问题
我们小时候就知道解方程的大致步骤:1.设未知数--->2.列方程--->3.解方程--->4.得到结果
问题:假设有两个未知数x和y,已知x+y=5且2x+3y=14,让我们求x和y分别是多少?(可能有的小伙伴会问了,你不会是个傻子吧,这还用编程计算?我口算都能算得出来,这里我只是给大家随便举了个简单的例子,大家别往心里去,主要目的是演示Z3用法 -。-)下面我们按照我们刚才的思路使用Z3进行编写:
1.设未知数:
from z3 import *
x = Int('x')
y = Int('y')
2.列方程:
s = Solver()
s.add(x+y==5)
s.add(2*x+3*y==14)
3.解方程判断是否有解
if s.check() == sat:
result = s.model()
4.输出方程的解,没有解则输出无解
print result
else:
print '无解'
可能到了这里大家就会觉得Z3好像也没啥方便的啊,这样的算法我列方程也能很快解出来啊。下面我再为大家演示一道题目,这道题是我学Z3的时候看到的一道公务员考试题目:

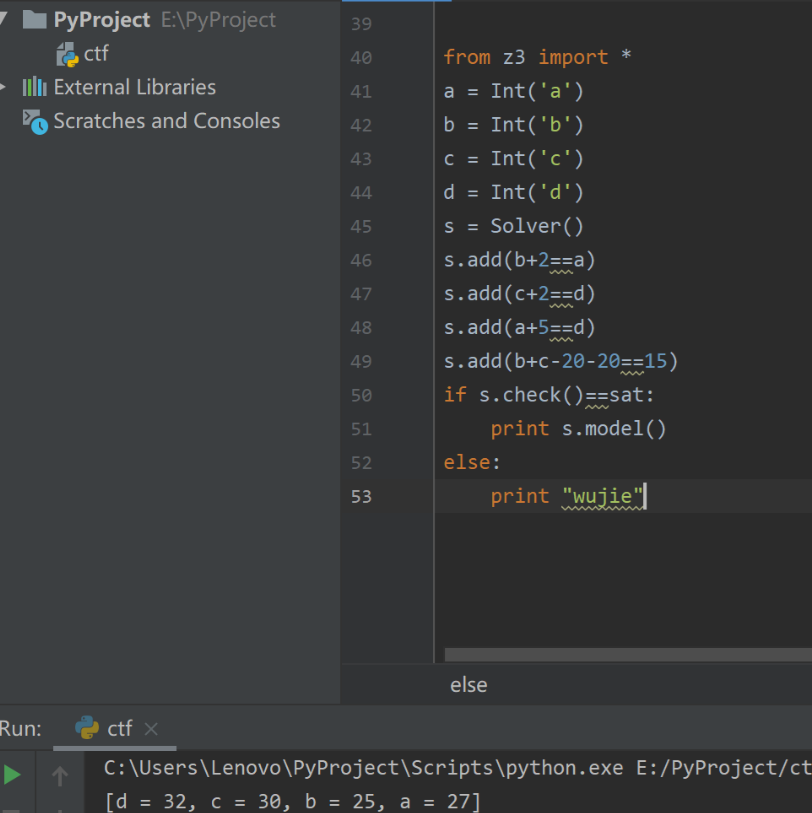
这个问题的逻辑比较复杂,比较绕,我们使用Z3来进行以下求解,同样我们也使用上面的解决步骤来:
我们设
a:2014年小李的年龄
b:小李弟弟的年龄
c:小王的年龄
d:小王哥哥的年龄
源码及运行结果如下:
开始练习
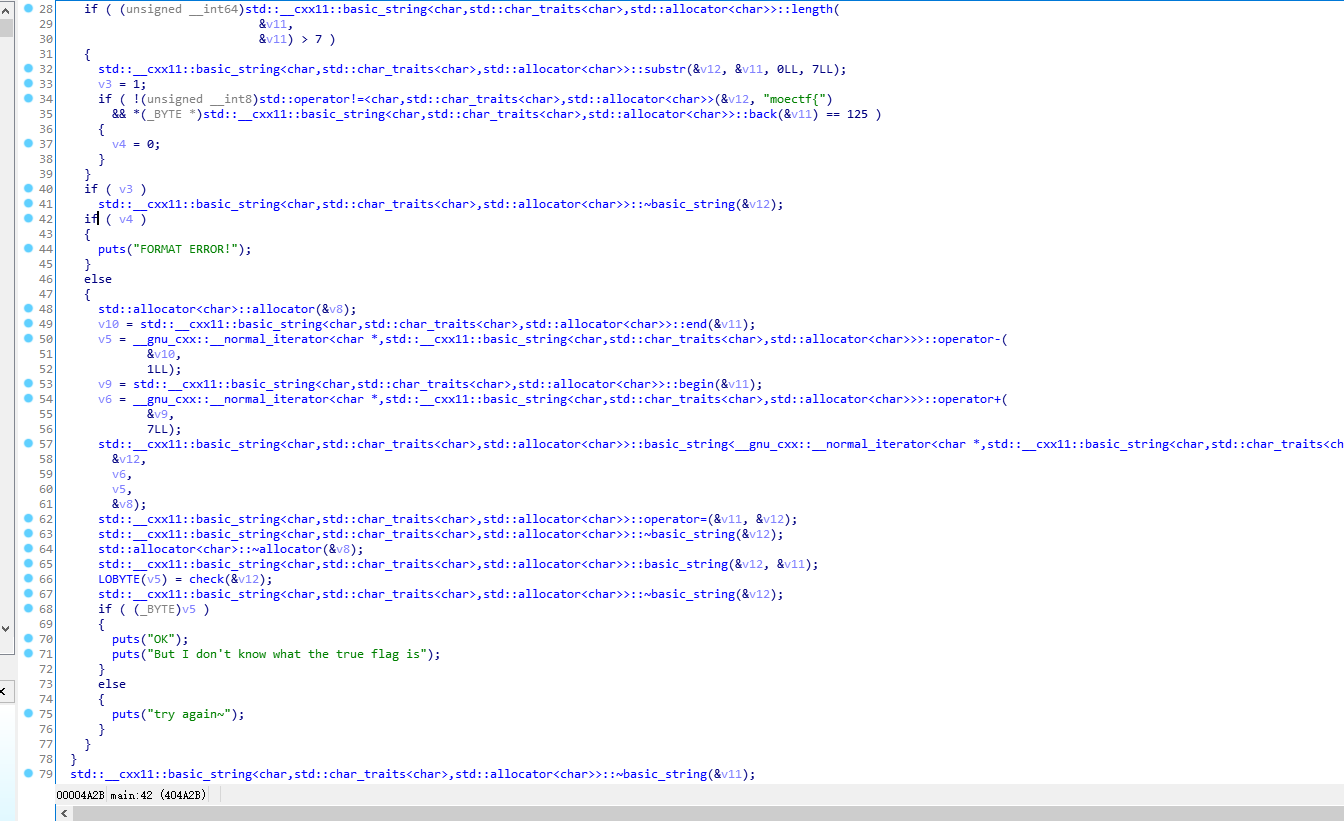
主要函数在
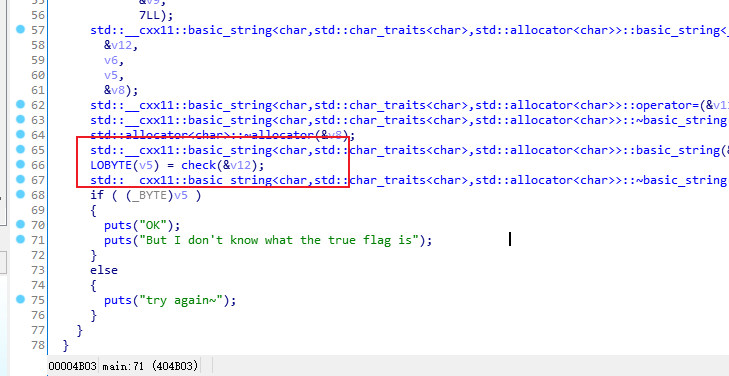
signed __int64 __usercall check@<rax>(__int64 a1@<rbp>, __int64 a2@<rdi>)
{signed int i; // [rsp-Ch] [rbp-Ch]__int64 v4; // [rsp-8h] [rbp-8h]__asm { endbr64 }v4 = a1;for ( i = 0; i <= 33; ++i ){check(std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>)::b[i] = 47806* (*(char *)std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::operator[](a2, i)+ i);if ( i )check(std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>)::b[i] ^= check(std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>)::b[i - 1] ^ 0x114514;check(std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>)::b[i] %= 51966;if ( check(std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>)::b[i] != a[i] )return 0LL;}return 1LL;
}
然后编写脚本
from z3 import *def solve_check_function():# ===== 1. 定义符号变量 =====s = [BitVec(f's_{i}', 8) for i in range(34)] # 34字节输入# ===== 2. 目标数组 a(从IDA提取) =====a = [0xB1B0, 0x5678, 0x7FF2, 0xA332, 0xA0E8, 0x364C, 0x2BD4,0xC8FE, 0x4A7C, 0x0018, 0x2BE4, 0x4144, 0x3BA6, 0xBE8C,0x8F7E, 0x35F8, 0x61AA, 0x2B4A, 0x6828, 0xB39E, 0xB542,0x33EC, 0xC7D8, 0x448C, 0x9310, 0x8808, 0xADD4, 0x3CC2,0x0796, 0xC940, 0x4E32, 0x4E2E, 0x924A, 0x5B5C]# ===== 3. 初始化Z3求解器 =====solver = Solver()# ===== 4. 模拟 b 数组的生成过程 =====b = [0] * 34for i in range(34):term = 47806 * (ZeroExt(24, s[i]) + i)if i == 0:b_i = termelse:b_i = term ^ (b[i-1] ^ 0x114514)b[i] = b_i % 51966solver.add(b[i] == a[i])# ===== 5. 约束输入为可打印ASCII字符 =====for c in s:solver.add(Or(And(c >= 0x20, c <= 0x7E), # 可打印ASCIIc == 0 # 或NULL字节))# ===== 6. 迭代求解所有可能的解 =====solutions = []while solver.check() == sat:model = solver.model()# 提取当前解solution = bytes([model.eval(s[i]).as_long() for i in range(34)])solutions.append(solution)print(f"Found solution: {solution.decode('latin-1')}")# 添加约束排除当前解,继续寻找其他解solver.add(Or([s[i] != model.eval(s[i]) for i in range(34)]))# ===== 7. 筛选最可能的Flag(moectf{...}格式) =====valid_flags = [sol for sol in solutions if sol.startswith(b'moectf{') and b'}' in sol]if valid_flags:print("\n[+] Probable valid Flags (moectf{...} format):")for flag in valid_flags:print(f" -> {flag.decode('latin-1')}")else:print("\n[-] No moectf{...} format solution found. All possible solutions:")for sol in solutions:print(f" -> {sol.decode('latin-1')}")if __name__ == "__main__":solve_check_function()
A cup of teA
可以了解一下TEA加密
TEA算法
TEA(Tiny Encryption Algorithm,微型加密算法)是一种对称密钥分组密码算法,由 David Wheeler 和 Roger Needham 于 1994 年在剑桥大学计算机实验室设计。它以简洁、高效著称,适用于资源受限的环境(如嵌入式系统)。以下是关于 TEA 的核心要点:
1. 基本特点
- 分组长度:64位(8字节)。
- 密钥长度:128位(16字节)。
- 结构:Feistel 网络(与DES类似),但更简单。
- 轮数:推荐32轮(平衡安全性与性能)。
- 无初始向量(IV):直接对明文分组加密,需配合模式(如CBC、CTR)使用。
2. 算法流程
加密过程(32轮迭代)
对64位明文分组 (L₀, R₀) 和128位密钥 K[0...3](4个32位子密钥):
复制
for i = 1 to 32:Rᵢ = Rᵢ₋₁ + (((Lᵢ₋₁ << 4) + K[0]) XOR (Lᵢ₋₁ + sum) XOR ((Lᵢ₋₁ >> 5) + K[1]))Lᵢ = Lᵢ₋₁ + (((Rᵢ << 4) + K[2]) XOR (Rᵢ + sum) XOR ((Rᵢ >> 5) + K[3]))sum += delta # delta = 0x9E3779B9(黄金比例常数)
最终输出 (L₃₂, R₃₂) 作为密文。
打开ida
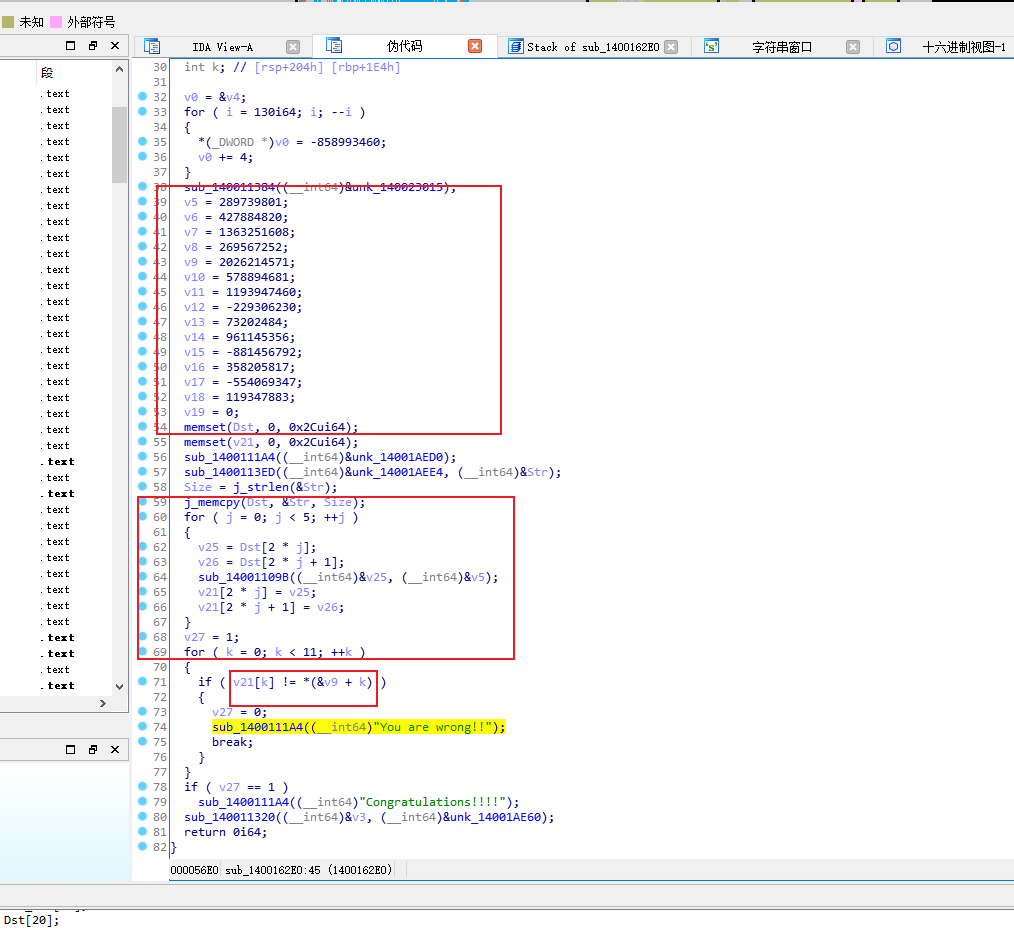
发现加密函数 sub_14001109B((__int64)&v25, (__int64)&v5);
进入函数
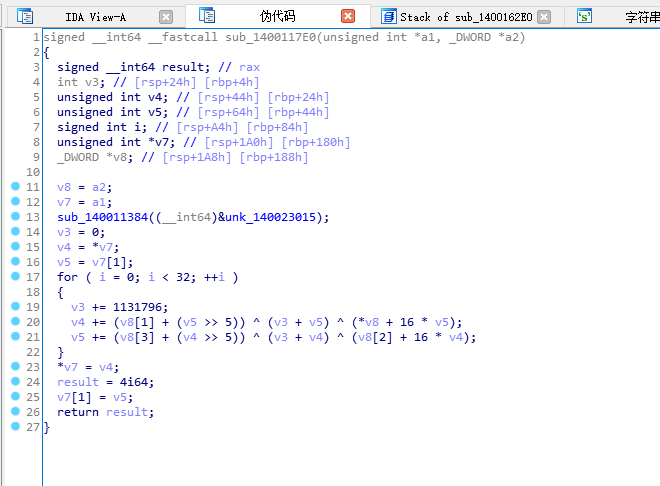
发现很像我们的tea
然后分析代码
题目给出了两个函数:第一个是主函数`sub_1400162E0`,第二个是TEA加密函数`sub_1400117E0`(在代码中通过`sub_14001109B`调用)。我们的目标是逆向TEA加密以获取flag。首先,分析主函数:1. 主函数中定义了一些变量,包括一个字符串`Str`(用户输入),以及两个数组`Dst`和`v21`。2. 通过`sub_1400113ED`函数获取用户输入,并存储在`Str`中,然后使用`memcpy`将输入复制到`Dst`数组(注意,`Dst`是`int`数组,而输入是`char`数组,所以这里会以4字节整数形式存储)。3. 然后,程序将输入分成5组(每组两个整数,即64位),每组都调用`sub_14001109B`(即TEA加密函数)进行加密,加密结果存储在`v21`数组中。4. 加密完成后,将`v21`数组与给定的一个数组(从`v9`到`v19`,共11个整数)进行比较。如果完全一致,则输出成功信息;否则输出错误。注意:给定的比较数组是:v9 = 2026214571v10 = 578894681v11 = 1193947460v12 = -229306230v13 = 73202484v14 = 961145356v15 = -881456792v16 = 358205817v17 = -554069347v18 = 119347883v19 = 0但是注意,在循环中比较的是`v21[k]`和`*(&v9 + k)`,即从`v9`的地址开始连续取11个整数(因为k从0到10)。现在,我们来看TEA加密函数(`sub_1400117E0`):该函数是标准的TEA加密,但做了一些修改(通常TEA使用32轮,这里也是32轮,但常数累加值不同)。函数参数:a1: 指向一个包含两个无符号整数的数组(待加密的数据块)a2: 指向一个包含4个整数的密钥数组(因为TEA的密钥是128位,即4个整数)在循环中:v3(初始为0)在每一轮增加一个常数(1131796)v4和v5分别是数据块的两个部分(v4是左部分,v5是右部分)加密过程如下:for (i=0; i<32; i++){v3 += 1131796;v4 += (a2[1] + (v5 >> 5)) ^ (v3 + v5) ^ (a2[0] + 16 * v5);v5 += (a2[3] + (v4 >> 5)) ^ (v3 + v4) ^ (a2[2] + 16 * v4);}在主函数中,调用加密函数时传递了两个参数:第一个是`(int64)&v25`(即指向一个包含两个整数的数组,初始为`v25`和`v26`,它们分别取自`Dst`数组的两个连续元素),第二个是`(int64)&v5`。注意,在主函数中,`v5`到`v8`是4个整数,然后`v9`到`v19`是另外的,但加密密钥是`&v5`,也就是从`v5`开始的4个整数:即`v5, v6, v7, v8`。主函数中给出的密钥值:v5 = 289739801v6 = 427884820v7 = 1363251608v8 = 269567252所以,密钥是:{289739801, 427884820, 1363251608, 269567252}加密后的结果应该等于给定的数组(从v9开始的11个整数,但注意我们加密了5个块,每个块两个整数,所以一共10个整数,而第11个整数是0(v19)?但是注意,在循环中比较了11个整数,而v19是0,所以v21[10]应该是0。然而,我们加密了5组(每组两个整数),所以v21[0]到v21[9]是加密结果,v21[10]没有赋值?但是注意,在循环中,j从0到4(5次),每次写入两个整数(2*j和2*j+1),所以v21[0..9]被赋值,而v21[10]没有被赋值,初始为0(因为前面有`memset(v21,0,0x2C)`,0x2C=44字节,即11个整数,所以v21[10]初始为0,而v19也是0,所以比较11个整数时,最后一个0相等。因此,我们有一个包含10个整数的密文(即v21[0]到v21[9]),和一个密钥(4个整数)。我们需要解密TEA得到原始的10个整数,然后将其转换为字符串(注意,原始输入被复制到Dst,而Dst是int数组,所以每个int对应4个字节,10个整数就是40个字节?但是用户输入的长度是`Size = strlen(&Str)`,所以输入字符串长度最多40(因为Dst有20个int,但只用了前10个?注意循环5组,每组两个整数,所以只处理了10个整数,即40字节。但实际输入可能不足40,但后面会补0(因为memset(Dst,0,0x2C))。解密思路:TEA解密是加密的逆过程。通常,TEA解密需要将加密过程的操作逆序进行,并注意减法。加密过程:v4 = left, v5 = rightfor i in range(32):v3 += delta (这里delta=1131796)v4 += (key[1] + (v5>>5)) ^ (v3 + v5) ^ (key[0] + (v5<<4))v5 += (key[3] + (v4>>5)) ^ (v3 + v4) ^ (key[2] + (v4<<4))注意:代码中写的是`*v8 + 16 * v5`,即`key[0] + 16*v5`,相当于左移4位(乘以16)。解密时,我们需要从最后加密完成的状态反向运算,而且v3的初始值在加密时是从0开始,每轮加1131796,所以32轮后v3的值为32*1131796。解密步骤(对于每个分组,两个整数):设加密后的左部分为v4_enc,右部分为v5_enc。在加密的最后,我们得到v4和v5,然后作为密文。解密时,我们需要从第31轮反向到第0轮,并且v3的初始值为32*1131796(即32轮的总和),然后每轮减去1131796。具体操作(参考标准TEA解密):v3 = 32 * 1131796 # 初始值v5 = v5_encv4 = v4_encfor i in range(32):v5 -= (key[3] + (v4>>5)) ^ (v3 + v4) ^ (key[2] + (v4<<4))v4 -= (key[1] + (v5>>5)) ^ (v3 + v5) ^ (key[0] + (v5<<4))v3 -= 1131796注意:这里先处理v5,然后处理v4,因为加密时是先更新v4,然后更新v5(所以反向时先更新v5,再更新v4)。但是注意:在加密过程中,第一轮先更新v4,然后更新v5;第二轮又更新v4,再更新v5,以此类推。所以解密时要从最后一轮开始反向,先撤销最后一轮对v5的更新,再撤销对v4的更新,然后倒数第二轮,等等。因此,解密循环应该按上述顺序。我们需要解密的密文是给定的11个整数(但第11个是0,我们只需要前10个):[2026214571, 578894681, 1193947460, -229306230, 73202484, 961145356, -881456792, 358205817, -554069347, 119347883]注意:这些整数在内存中是按照小端序存储的吗?但是题目没有说明,而且我们在x64环境下(小端序),但整数在代码中是以整数形式给出的,所以直接使用即可。但是注意,在加密函数中,使用的是无符号整数运算,而这里给出的整数有负数,所以我们需要将其转换为无符号整数(即模2^32)。例如:2026214571 -> 无符号就是它本身(正数)-229306230 -> 无符号:2^32 - 229306230 = 4065661066(因为负数用补码表示)我们可以用Python的ctypes.c_uint来处理。步骤:1. 将密文分成5组,每组两个整数(64位)。2. 对于每组,使用TEA解密(密钥为[289739801,427884820,1363251608,269567252])得到两个整数(原始输入)。3. 将5组解密后的整数按顺序连接起来,得到一个整数数组(10个整数)。4. 将每个整数按小端序转换为4个字节(因为整数是4字节的),然后拼接成字符串(注意,整数在内存中是按小端序存储的,但我们在解密时直接使用整数,而原始输入是字符串复制到整数数组,所以每个整数对应4个字符,顺序可能是小端序?这取决于复制方式。但是注意,主函数中:j_memcpy(Dst, &Str, Size);这里,`Str`是一个字符串(字节数组),`Dst`是`int`数组(每个int占4字节)。在x64小端序机器上,字符串按字节顺序复制到整数中,即:Dst[0] = Str[0] | Str[1]<<8 | Str[2]<<16 | Str[3]<<24 (小端序:第一个字节在最低位)所以,当我们解密得到整数后,需要将每个整数拆分为4个字节(按小端序),然后拼接。例如,整数0x61626364(小端序)对应的字符串是"dcba",但实际我们希望得到原始字符串顺序,所以应该按照小端序转换:即整数0x61626364在内存中是64,63,62,61(十六进制),对应字符串"dcba",而实际上原始字符串应该是"abcd"被存储为0x64636261(大端序)?不对,这里存在误解。在内存中,字符串"abcd"存储为:'a','b','c','d'(地址递增)。当复制到整数数组时:第一个整数(Dst[0])在内存中占4个字节,地址从低到高:'a','b','c','d',那么整数表示为0x64636261(因为高位在高地址,低位在低地址,所以小端序的整数是0x64636261,即'd'在高位,'a'在低位?不对,小端序是低地址存低位,所以:地址最低的字节是整数的低8位,所以:地址0: 'a' -> 0x61 -> 低位地址1: 'b' -> 0x62地址2: 'c' -> 0x63地址3: 'd' -> 0x64 -> 高位所以整数 = 0x64636261 (因为高位是0x64,低位是0x61)?不对,小端序的整数表示应该是:0x64636261,但如果我们直接打印这个整数,它在内存中的字节顺序(从低到高)是61,62,63,64,即字符串"abcd"的逆序?不对,应该是:在内存中:低地址->高地址:61,62,63,64 -> 字符串"abcd"。而整数0x64636261在内存中的表示(从低到高)是61,62,63,64,所以它对应的字符串(按地址顺序)就是"abcd"。因此,当我们从整数转换为字节时,我们只需按小端序拆分:即整数的低8位对应第一个字节,然后下一个8位对应第二个字节,以此类推。这样得到的4个字节,按地址递增顺序排列就是原始字符串。所以,对于每个整数,我们将其转换为4个字节(小端序):byte0 = (n ) & 0xFFbyte1 = (n >> 8) & 0xFFbyte2 = (n >> 16) & 0xFFbyte3 = (n >> 24) & 0xFF然后,将这四个字节按顺序(byte0, byte1, byte2, byte3)拼接,就得到原始的4个字符。但是,因为我们的整数数组是连续的,所以整个字符串就是10个整数转换后的字节按顺序拼接。另外,注意用户输入的长度(Size)可能小于40(最多40),所以字符串末尾可能有0(因为memset(Dst,0,0x2C)),所以转换后需要去掉末尾的0。现在,我们开始编写解密脚本。首先,定义密钥和密文:key = [289739801, 427884820, 1363251608, 269567252]注意:在加密函数中,key[0]和key[1]用于更新v4,key[2]和key[3]用于更新v5。密文(分组):group0: [2026214571, 578894681]group1: [1193947460, -229306230] -> 注意负数:-229306230的32位无符号表示为 0xE75E0C0A(通过补码计算:-229306230 = 0xE75E0C0A,因为229306230的十六进制是0x0DA1F3F6,取反加1得到0xF25E0C0A?不对,我们直接用Python转换:2**32-229306230=4065661066,即0xF25E0C0A?)但是,在Python中,我们可以用ctypes.c_uint来处理,但这里为了简单,我们直接使用模运算:在32位无符号整数运算中,负数等同于其无符号表示。在Python中,我们可以使用& 0xFFFFFFFF来得到32位无符号表示。例如:-229306230 & 0xFFFFFFFF = 4065661066所以,密文数组(10个整数)的无符号表示为:[2026214571, 578894681, 1193947460, 4065661066, 73202484, 961145356, 3413510504, 358205817, 3740897949, 119347883]注意:第6个数:-881456792 & 0xFFFFFFFF = 3413510504第8个数:-554069347 & 0xFFFFFFFF = 3740897949然后,我们写TEA解密函数。注意:加密时使用的v3初始为0,每轮加上1131796(32轮)。所以解密时v3的初始值为32*1131796,然后每轮减去1131796。但是,注意:1131796 * 32 = 36217472,这个值可能超过32位整数范围?1131796*32=36217472,在32位无符号整数范围内(0~4294967295)。解密函数(针对一个分组,即两个无符号整数):def tea_decrypt(v4, v5, key):delta = 1131796v3 = delta * 32 # 32轮累加值for i in range(32):# 先撤销对v5的更新(注意,加密时最后一轮更新了v5,所以解密时第一轮就要撤销v5)v5 = (v5 - ((key[3] + (v4<<4)) ^ (v4 + v3) ^ (key[2] + (v4>>5))) & 0xFFFFFFFF# 然后撤销对v4的更新v4 = (v4 - ((key[1] + (v5<<4)) ^ (v5 + v3) ^ (key[0] + (v5>>5))) & 0xFFFFFFFFv3 = (v3 - delta) & 0xFFFFFFFF # 注意,v3也需要保持在32位范围内return v4, v5但是,等一下,这个公式和加密的公式不完全对应?我们来看加密的公式:v4 += (key[1] + (v5>>5)) ^ (v3 + v5) ^ (key[0] + 16*v5) # 16*v5 即 v5<<4v5 += (key[3] + (v4>>5)) ^ (v3 + v4) ^ (key[2] + 16*v4) # 16*v4 即 v4<<4所以,在解密时,我们需要:v5 -= ( (key[3] + (v4>>5)) ^ (v3 + v4) ^ (key[2] + (v4<<4)) v4 -= ( (key[1] + (v5>>5)) ^ (v3 + v5) ^ (key[0] + (v5<<4))注意:在解密循环中,我们使用的是当前轮次的v3(即从大到小),而且先更新v5(使用当前的v4,这个v4是上一轮解密后的v4,但第一轮时v4是加密后的左半部分,还没有改变),然后更新v4(使用刚刚更新后的v5)。但是,在加密时,一轮中先更新v4(使用旧的v5),然后更新v5(使用新的v4)。所以解密时,一轮中先更新v5(使用旧的v4和旧的v5?)不对,这里应该注意顺序。实际上,解密过程应该和加密过程完全相反,并且使用相同的v3值(但是顺序倒过来)。标准TEA解密(参考):for (i=0; i<32; i++) {sum = delta * 32; // 初始为加密的总和for (i=0; i<32; i++) {y -= ((z << 4) + k[2]) ^ (z + sum) ^ ((z >> 5) + k[3]);z -= ((y << 4) + k[0]) ^ (y + sum) ^ ((y >> 5) + k[1]);sum -= delta;}}但是,注意我们代码中加密的顺序是:v4 += ... (使用v5)v5 += ... (使用v4,这个v4是更新后的)而标准TEA中,一轮中先更新y(即v5)?不对,标准TEA中:v0 += ((v1<<4)+k0) ^ (v1+sum) ^ ((v1>>5)+k1);v1 += ((v0<<4)+k2) ^ (v0+sum) ^ ((v0>>5)+k3);但我们的代码是:v4(左)先更新,然后v5(右)再更新(使用新的v4)。所以我们的加密顺序和标准TEA一样。因此,解密时:for i in range(32):v5 -= (key[3] + (v4>>5)) ^ (v3 + v4) ^ (key[2] + (v4<<4))v4 -= (key[1] + (v5>>5)) ^ (v3 + v5) ^ (key[0] + (v5<<4))v3 -= delta但是,注意:在解密第一轮时,v4和v5是密文的两个部分(即加密后的结果)。我们使用这个v4(加密后的v4)来解密v5(得到加密前一轮的v5),然后用这个解密得到的v5来解密v4(得到加密前一轮的v4)。然后v3减去delta,进入下一轮。因此,解密函数写为:def tea_decrypt(v4, v5, key):delta = 1131796total = delta * 32for i in range(32):v5 = (v5 - ((key[3] + (v4 >> 5)) ^ (total + v4) ^ (key[2] + (v4 << 4)))) & 0xFFFFFFFFv4 = (v4 - ((key[1] + (v5 >> 5)) ^ (total + v5) ^ (key[0] + (v5 << 4)))) & 0xFFFFFFFFtotal = (total - delta) & 0xFFFFFFFFreturn v4, v5注意:减法操作后要取32位(即&0xFFFFFFFF),因为Python整数不会自动截断。然后,我们将10个整数(密文)分成5组,每组两个整数,分别调用tea_decrypt。最后,将每个分组解密得到的两个整数转换为4个字节(小端序),然后拼接成字符串。注意:最后一个整数解密后可能是0(因为原始输入可能不足40字节,后面补0),所以得到字符串后,我们可能需要去掉末尾的0。现在,我们用Python实现。步骤:1. 定义密钥和密文(无符号32位整数形式)。2. 定义TEA解密函数。3. 分组解密。4. 将每个整数转换为4字节的小端序字符串。5. 拼接所有字符串,并去掉末尾的0。以下是针对该逆向题目的详细分析和解密脚本,用于获取flag。题目使用TEA加密算法对用户输入进行加密,并与预设的密文比较。
关键信息总结:
-
密钥:
[289739801, 427884820, 1363251608, 269567252](对应主函数中的v5到v8) -
密文:11个整数(主函数中的
v9到v19),实际有效密文为前10个整数(最后1个是0):text
[2026214571, 578894681, 1193947460, -229306230, 73202484, 961145356, -881456792, 358205817, -554069347, 119347883] -
加密过程:输入被分成5组(每组64位),每组使用TEA加密(32轮)
-
解密需求:逆向TEA算法解密密文,还原原始输入字符串
TEA解密算法原理:
-
加密时每轮操作:
c
v4 += (key[1] + (v5 >> 5)) ^ (v3 + v5) ^ (key[0] + 16 * v5); v5 += (key[3] + (v4 >> 5)) ^ (v3 + v4) ^ (key[2] + 16 * v4); v3 += 1131796; // Delta -
解密时逆向操作(从最后一轮开始反向计算):
python
total = 32 * delta # 初始为加密结束时的v3 for _ in range(32):v5 -= (key[3] + (v4 >> 5)) ^ (total + v4) ^ (key[2] + (v4 << 4))v4 -= (key[1] + (v5 >> 5)) ^ (total + v5) ^ (key[0] + (v5 << 4))total -= delta
Python解密脚本:
python
def tea_decrypt(v4, v5, key):delta = 1131796total = (delta * 32) & 0xFFFFFFFFfor _ in range(32):# 逆向更新v5(使用当前v4)v5 = (v5 - ((key[3] + (v4 >> 5)) ^ (total + v4) ^ (key[2] + (v4 << 4)))) & 0xFFFFFFFF# 逆向更新v4(使用当前v5)v4 = (v4 - ((key[1] + (v5 >> 5)) ^ (total + v5) ^ (key[0] + (v5 << 4)))) & 0xFFFFFFFFtotal = (total - delta) & 0xFFFFFFFFreturn v4, v5# 密钥(4个32位整数)
key = [289739801, 427884820, 1363251608, 269567252]# 密文(转换为无符号32位整数)
cipher = [2026214571, 578894681,1193947460, 4065661066, # -229306230 -> 406566106673202484, 961145356,3413510504, 358205817, # -881456792 -> 34135105043740897949, 119347883 # -554069347 -> 3740897949
]# 分组解密(每组2个整数)
plain_ints = []
for i in range(0, len(cipher), 2):v4, v5 = cipher[i], cipher[i+1]dec_v4, dec_v5 = tea_decrypt(v4, v5, key)plain_ints.extend([dec_v4, dec_v5])# 将整数转换为小端序字节串
flag_bytes = b''
for num in plain_ints:flag_bytes += bytes([num & 0xFF, # 字节0(最低位)(num >> 8) & 0xFF, # 字节1(num >> 16) & 0xFF, # 字节2(num >> 24) & 0xFF # 字节3(最高位)])# 移除末尾填充的NULL字节
flag = flag_bytes.rstrip(b'\x00').decode('ascii')
print(f"Flag: {flag}")
maze地图游戏
W:向上走 A:向左走 D:向右走 S:向下走 不会做了可以玩玩游戏
打开程序发现字符串中就有地图
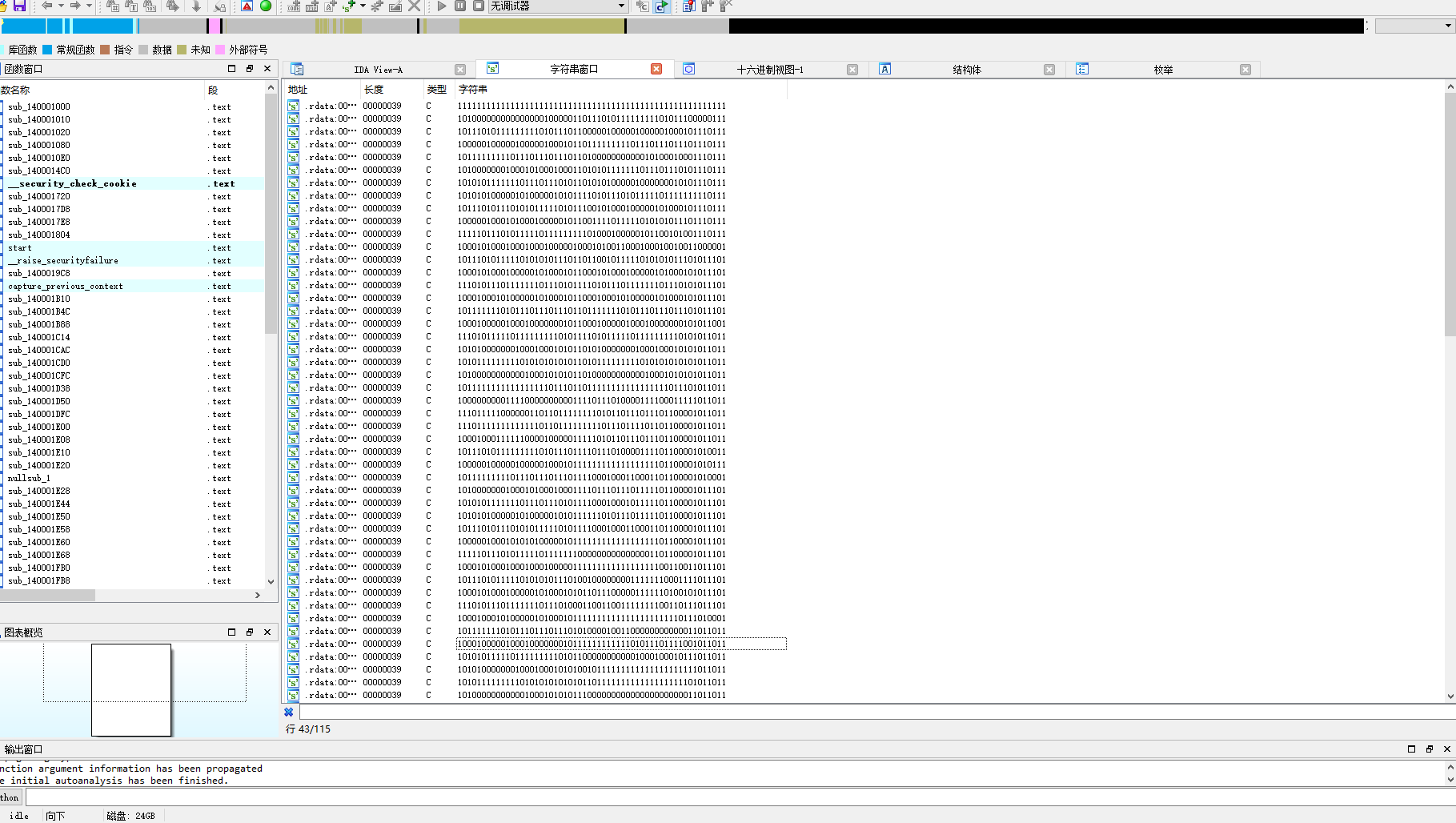
然后把地图导出来
再看函数

可以看出是从(1,1)开始
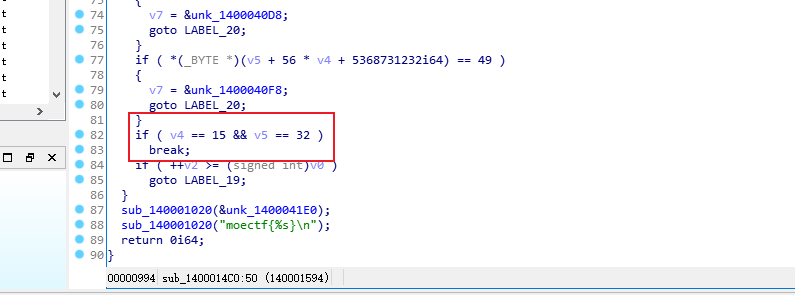
到(15,32)结束
我们借助工具
github:https://github.com/LingerJAB/MazeSolver
在地图(1,1)上表示为Sj结尾表示E
打开工具
然后求解

moectf{SSDDDDWWDDSSDDDDSSDDSSSSDDWWDDWWDDWWWWDDDDSSSSAASSSSAAAASSAASSAAWWAAWWWWAAAASSDDSSAASSDDSSSSAAAASSDDDDDDWWWWDDDDSSDDDDWWDDWWAAWWDDDDSSSSSSSSSSSSAAASSSDDDSSSSAASSSSAAAASSAASSAAWWAAWWWWAAAASSDDSSAASSDDSSSSAAAASSDDDDDDWWWWDDDDSSDDDDWWDDWWAAWWDDDDSSSSSSSSSSSSAAAWAWWWAASSAAWWAASSAAAAAAAAAAWWWWAASSSSSSDDDDSSSSSSDDDDDDDDDWWDDDSSDDWWWDDDSSSDDDDDWWAWWDDDDDDDDDDDDDDDDDDDDSSDDDDDDDDWWWWAWWWWWWWWDWWWWWWWWWWWAAWWDWWWWWWWWWWDWWWWWWAAAASSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSAAAWWAAAAAAAAAAAAAAAAAAAWWWDDDDDDDDWWDDDDDDDDDDWWWAWAAWAWWWWWWWWWWWWWDDWWWWAASSAAWWAASSAAAAAAAAAAWWWWAAWWDDWWAAWWDWWWDWWWWDDDDDDDDDDSSDDDDSSSSDSDSSDDSSAASSAAAAWWAAAASSSSAAAAAAWWDDDDWWWWAAWWAWAASSDSSSDD}
flows花指令
moectf 逆向
打开ida,发现solve()这个函数打不开,F5已经失效。
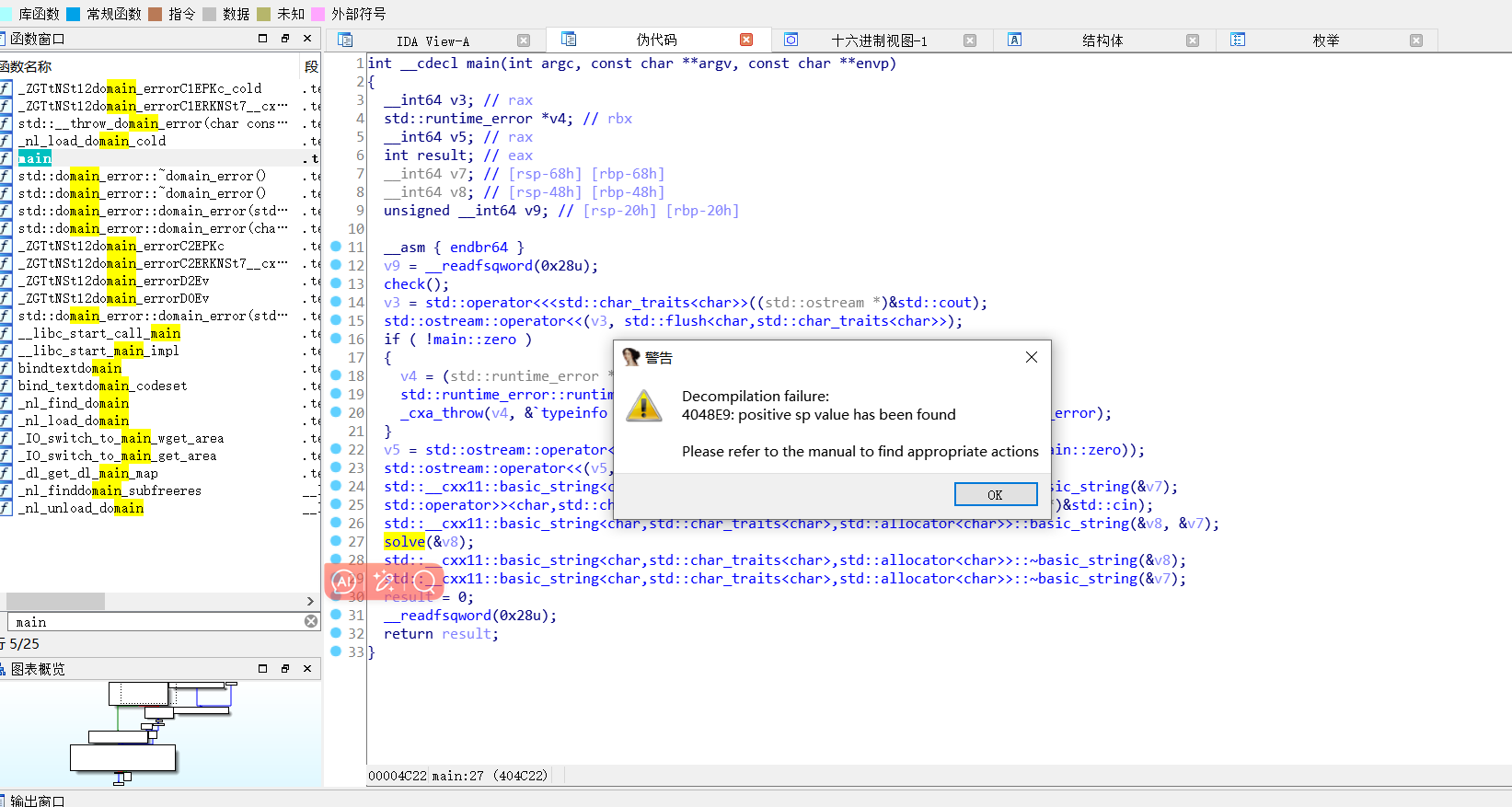
然后去找solve按住空格
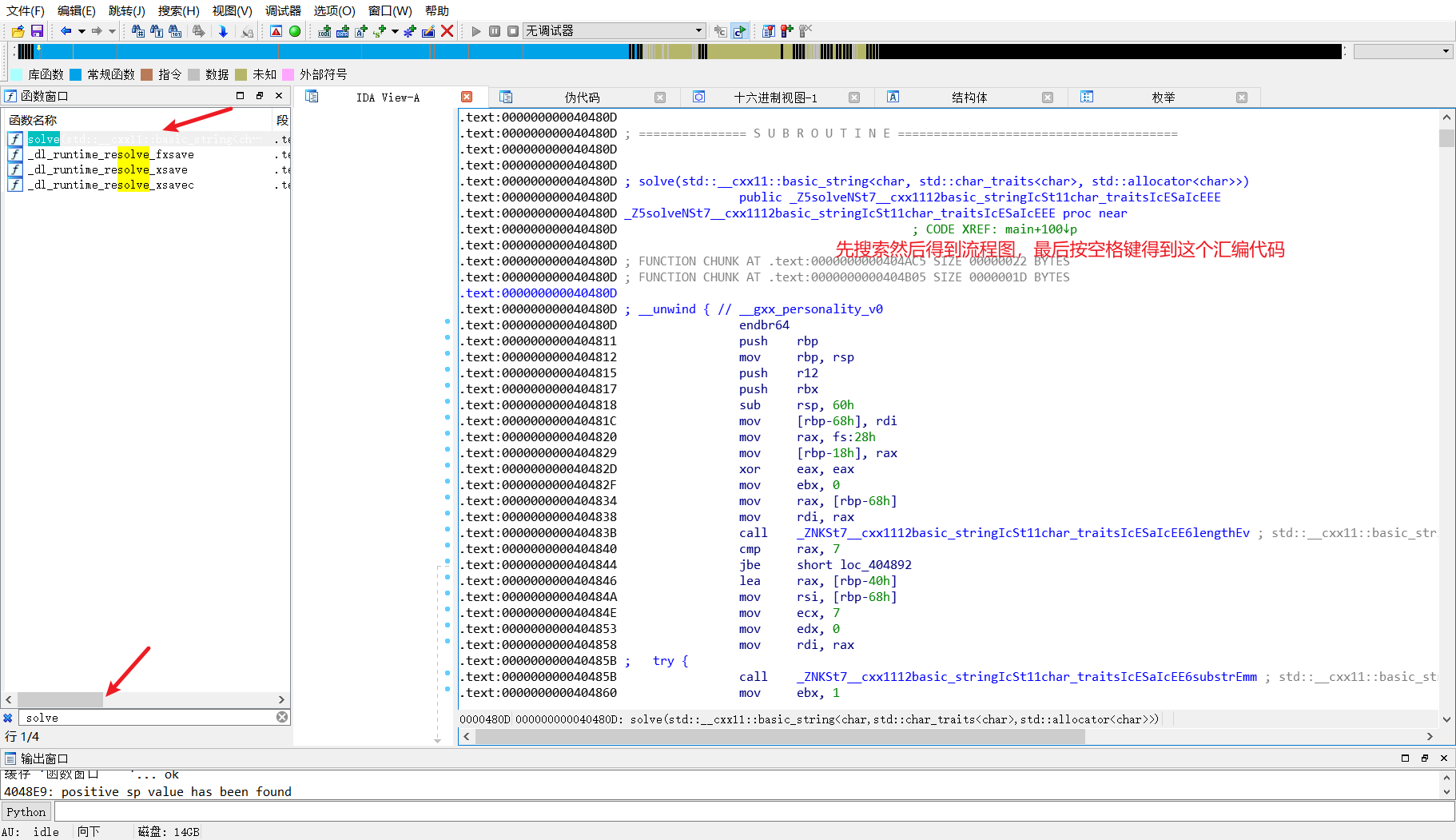
然后找到错误的地方
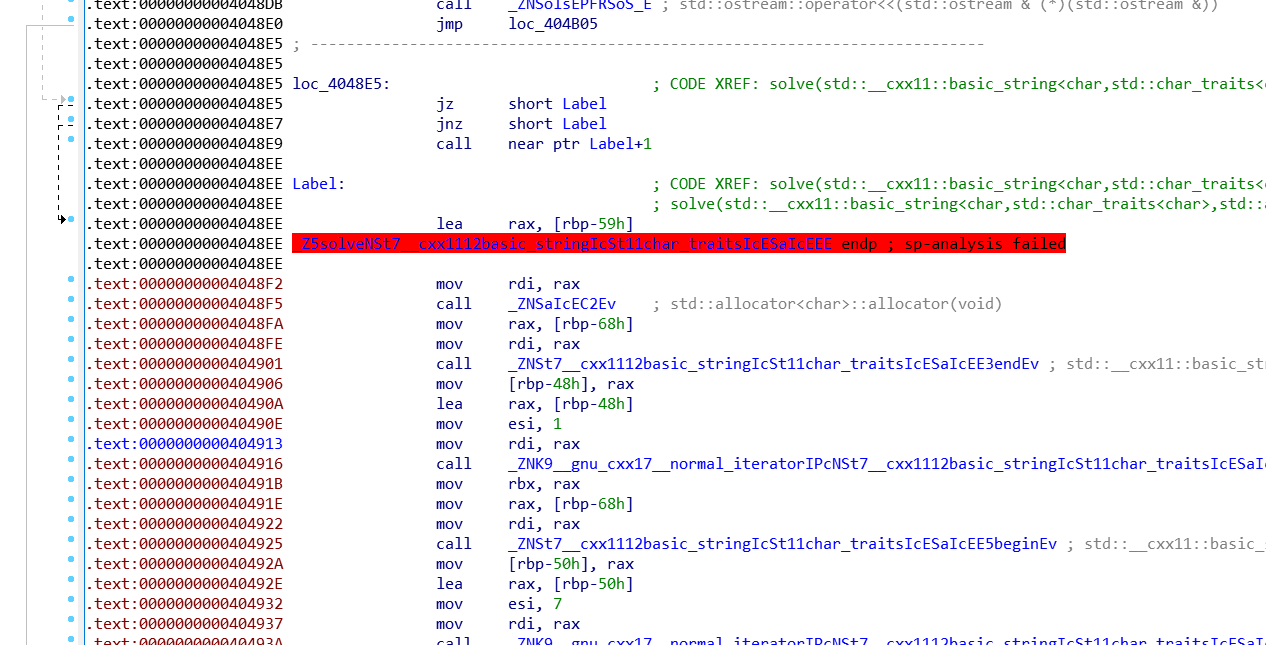
这个jz jnz是跳转,ida反汇编是递归扫描的,说白了就是没条指令都会扫描,然后反汇编
相当于没有什么样
然后直接把让其都变成nop就行了
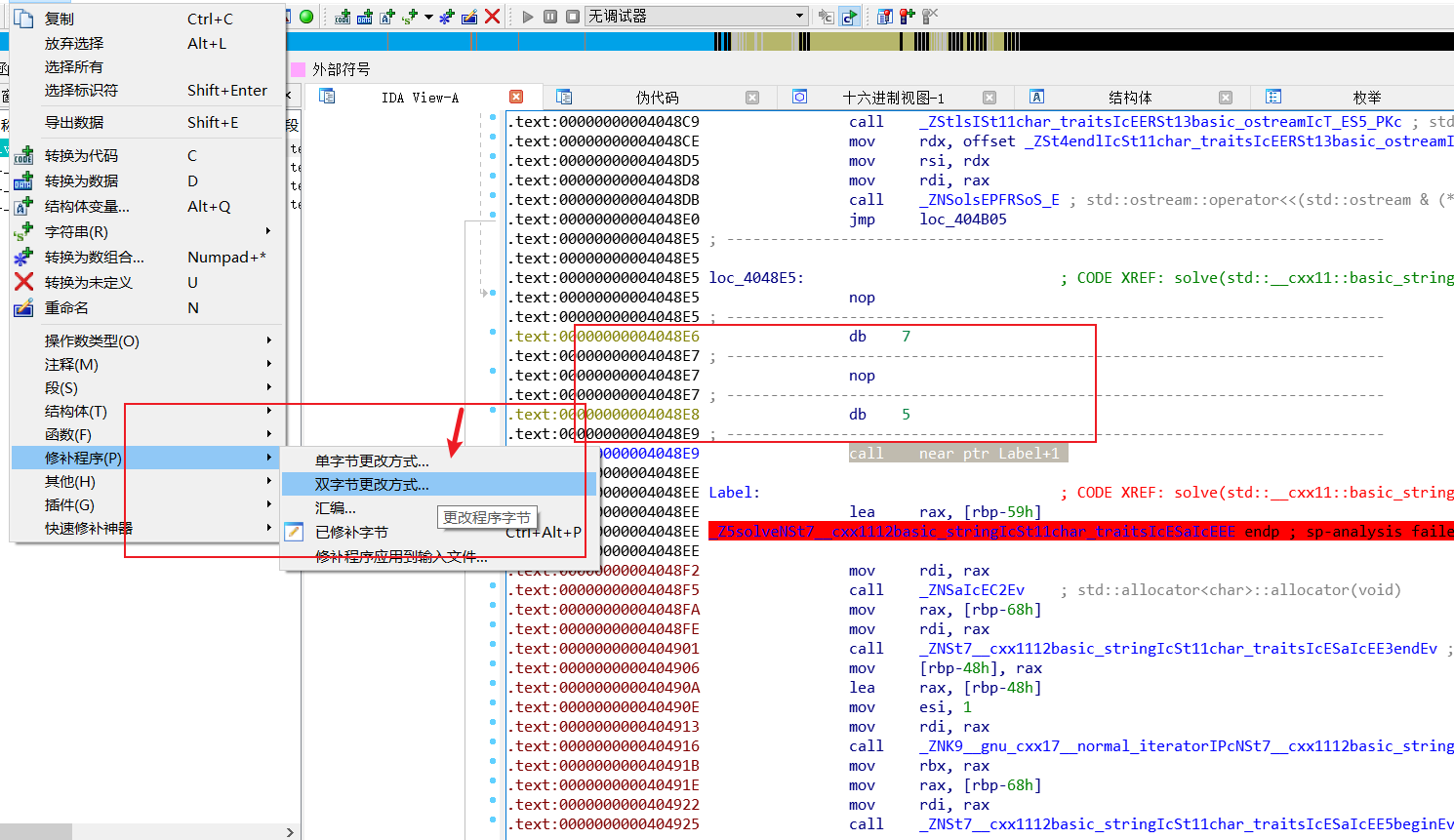
然后把函数重新加载一下
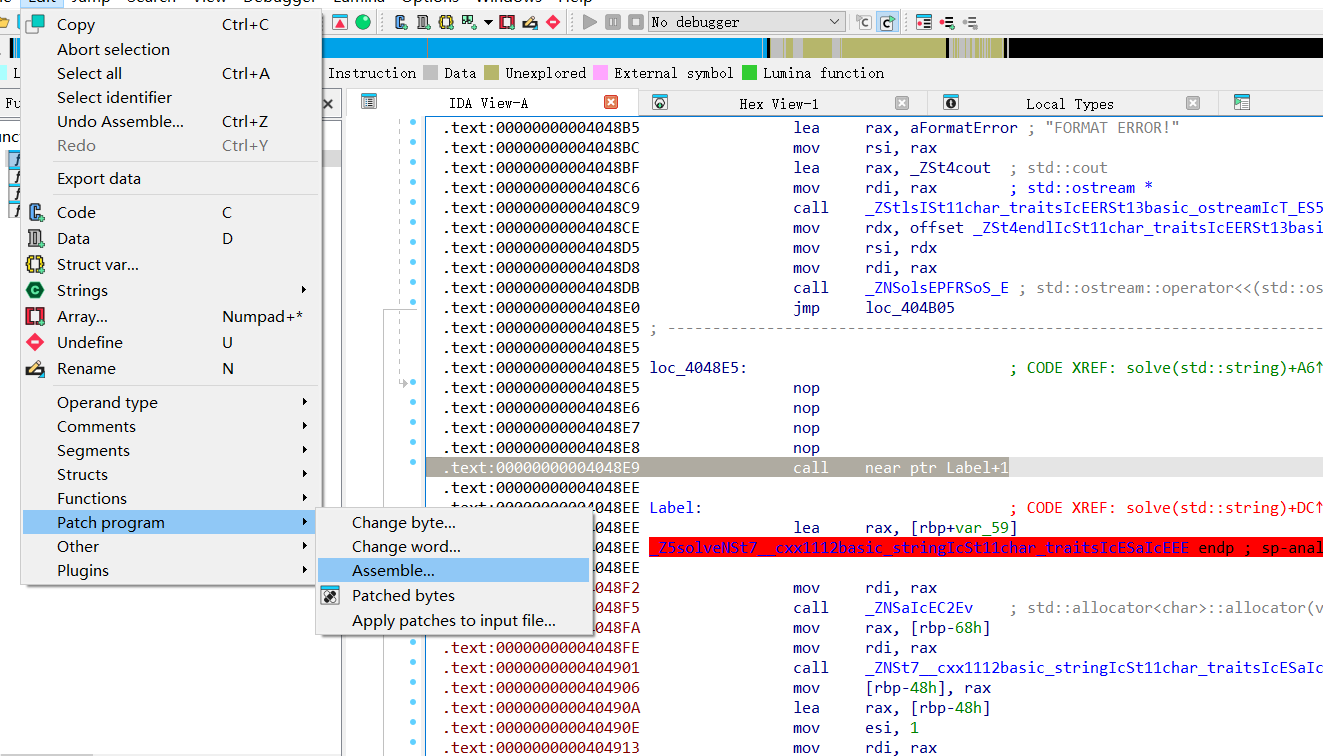
清理到这个差不多
然后更新函数
按一下u和按一下p
发现可以进去solve
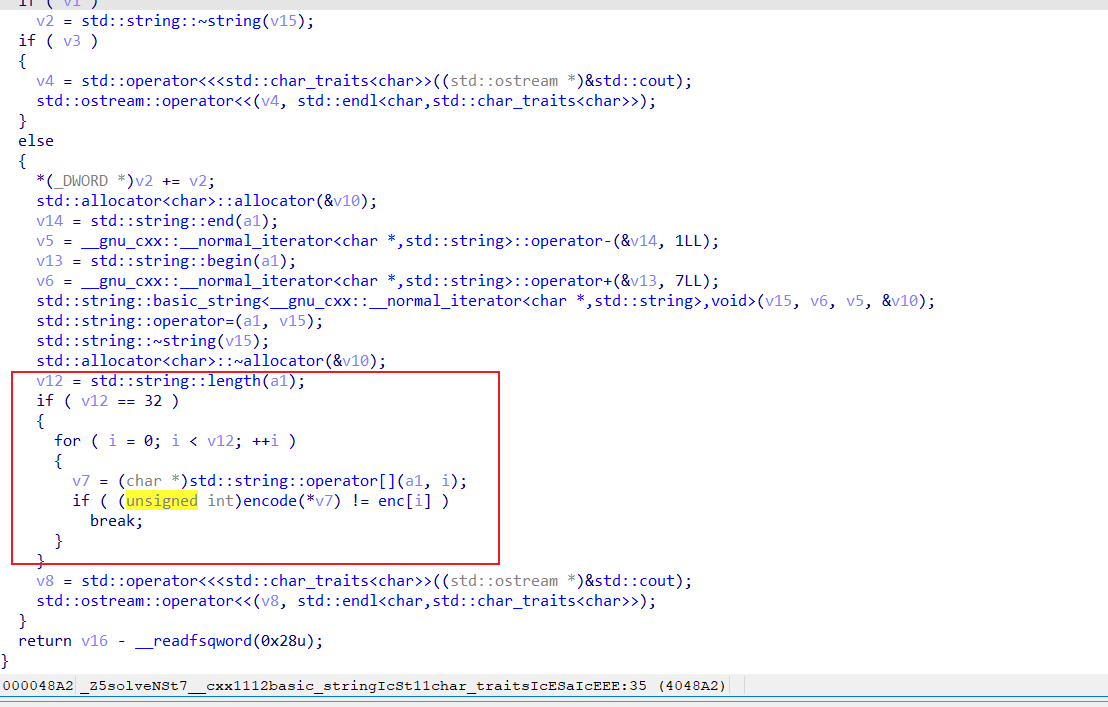
主要函数在这里
查看encode和数据,但是key这里有一个坑,之前被修改过,有两个调用
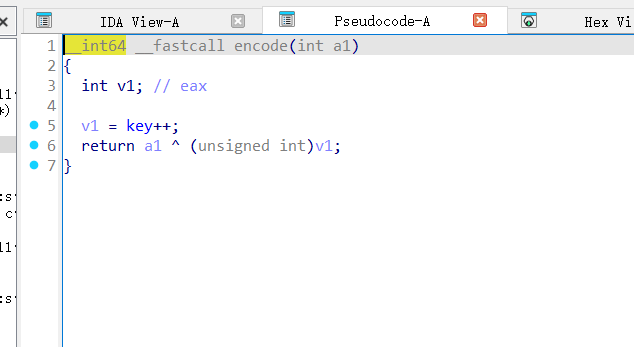
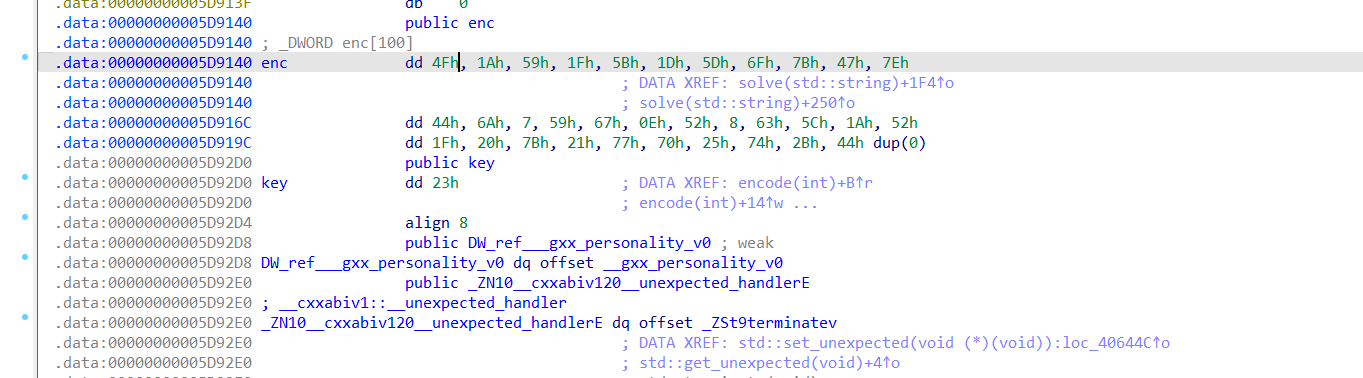
按x交叉应用
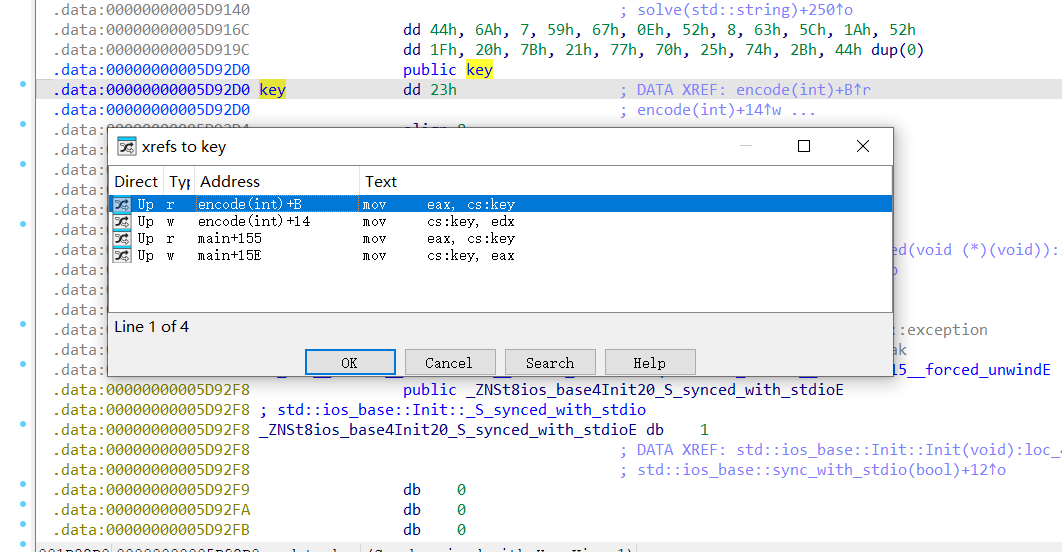
找到其他地方对其进行篡改的地方
发现eor了别的数
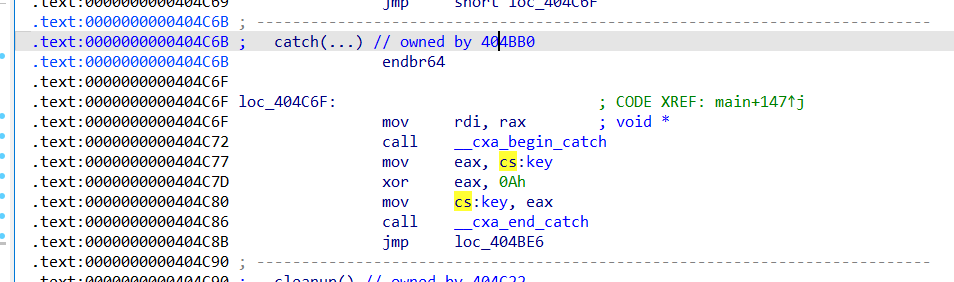
然后写代码
enc = [0x4F, 0x1A, 0x59, 0x1F, 0x5B, 0x1D, 0x5D, 0x6F, 0x7B, 0x47, 0x7E, 0x44, 0x6A, 0x07, 0x59, 0x67, 0x0E, 0x52, 0x08, 0x63, 0x5C, 0x1A, 0x52, 0x1F, 0x20, 0x7B, 0x21, 0x77, 0x70, 0x25, 0x74, 0x2B]# key初始值经过异常处理修改:0x23 ^ 0x0A = 0x29
key = 0x23 ^ 0x0A # 0x29flag_inner = ""
for i in range(len(enc)):flag_char = enc[i] ^ keyflag_inner += chr(flag_char)key += 1flag = "moectf{" + flag_inner + "}"
print(flag)
moectf{f0r3v3r_JuMp_1n_7h3_a$m_a9b35c3c}
ezandroid逆向
用jdx打开文件
寻找函数入口
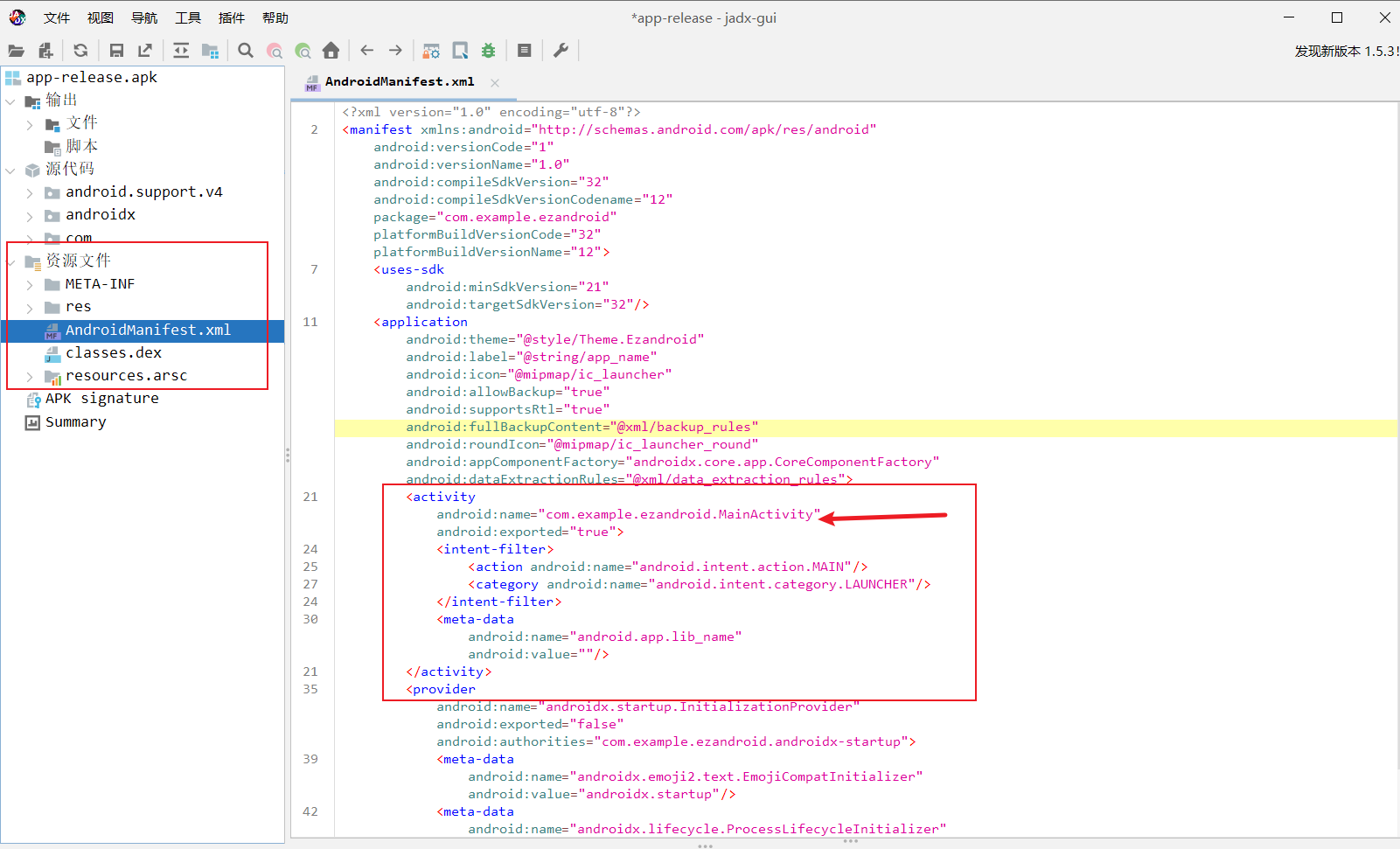
打开入口
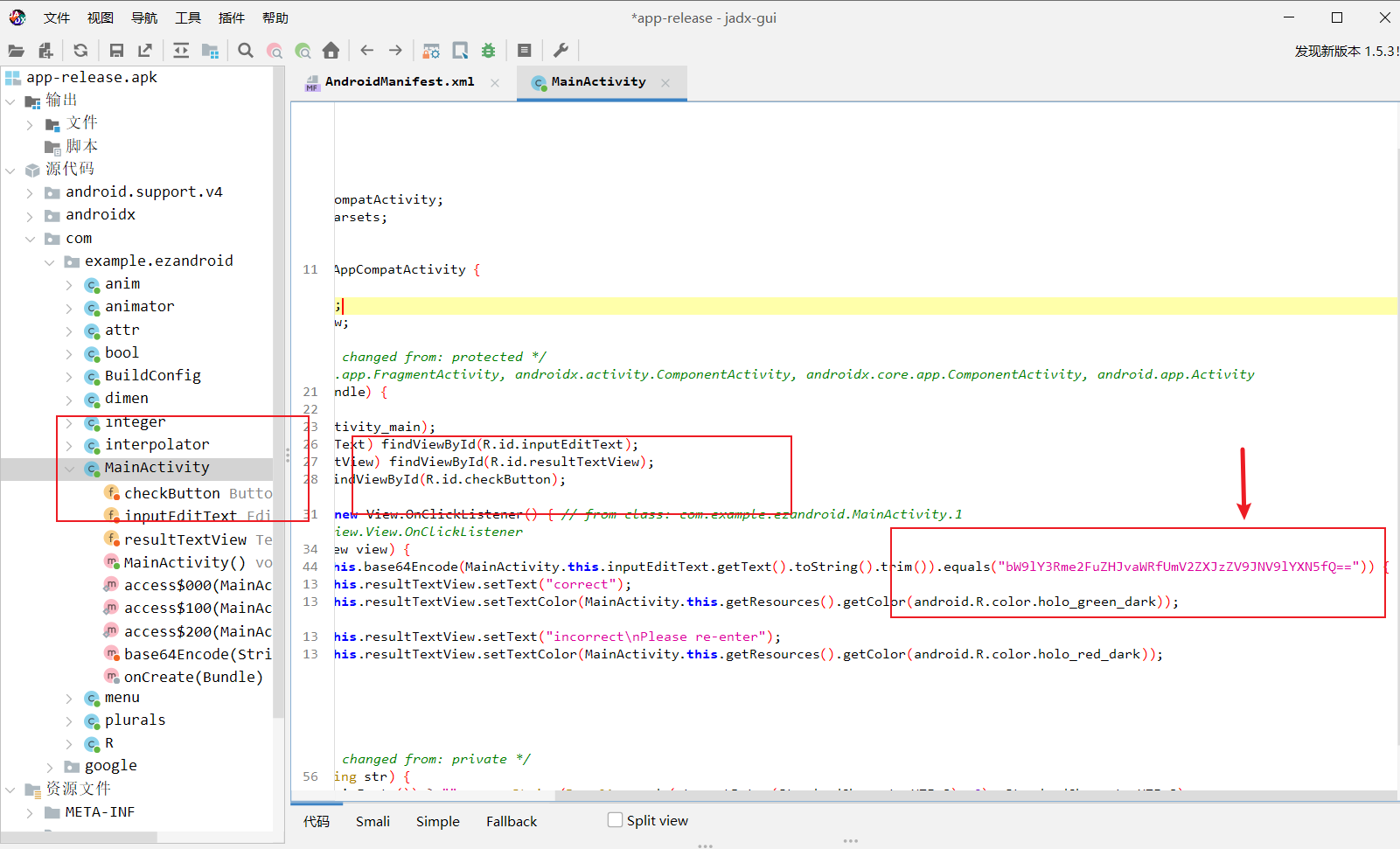
发现是base64
bW9lY3Rme2FuZHJvaWRfUmV2ZXJzZV9JNV9lYXN5fQ==
moectf{android_Reverse_I5_easy}
catch
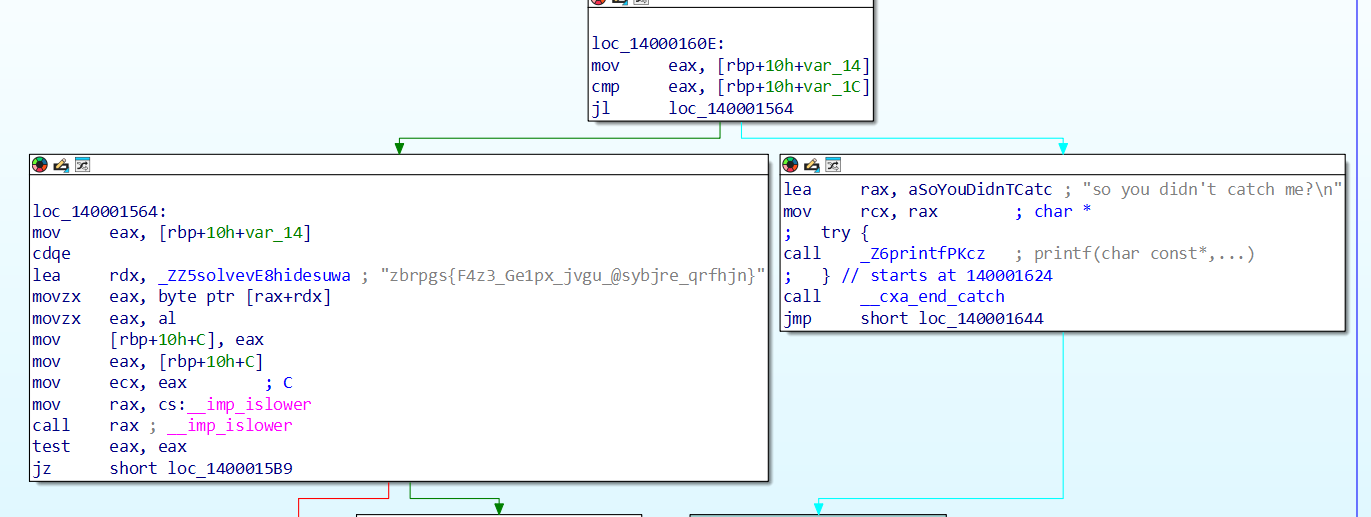
别在外面包 try/catch,让异常飞进 solve(),程序自己会打印 ROT13 的 flag;解密即得
import codecs
import sysdef rot13(text: str) -> str:"""标准 ROT13 解密(加密即解密)"""return codecs.encode(text, "rot13")if __name__ == "__main__":cipher = "zbrpgs{F4z3_Ge1px_jvgu_@sybjre_qrfhjn}"plain = rot13(cipher)print("Cipher:", cipher)print("Plain :", plain)
moectf{S4m3_Tr1ck_with_@flower_desuwa}
have_fun
这是一个Windows对话框程序,用户需要输入一个flag,程序会进行验证。从代码分析可以看出这是一个简单的XOR加密验证题目。
逐个加密
v23[v14] = String[v14] ^ 0x2A; // 直接与0x2A异或
验证比较
v16 = *(unsigned __int16 *)((char *)v15 + (char *)aGeoiLqbj - (char *)v23);
v17 = *v15 - v16;
将加密后的输入与硬编码数据 aGeoiLqbj 进行比较
这是一个对称加密:
- 加密:
明文 ^ 0x2A = 密文 - 解密:
密文 ^ 0x2A = 明文
因为 XOR 操作是可逆的:(A ^ B) ^ B = A
# 目标密文
ciphertext = "GEOI^LQbj\\\x1EuL\x7FDW"# XOR解密
flag = ''.join(chr(ord(c) ^ 0x2A) for c in ciphertext)
print(flag) # 输出: moectf{H@v4_fUn}
upx_revenge
打开查壳,发现是upx壳,尝试脱壳失败,直接去网上搜索原因,是因为upx特征修改了,使用upx -d 文件名.exe无法脱壳,需要进行upx特征修复
这个是正常的
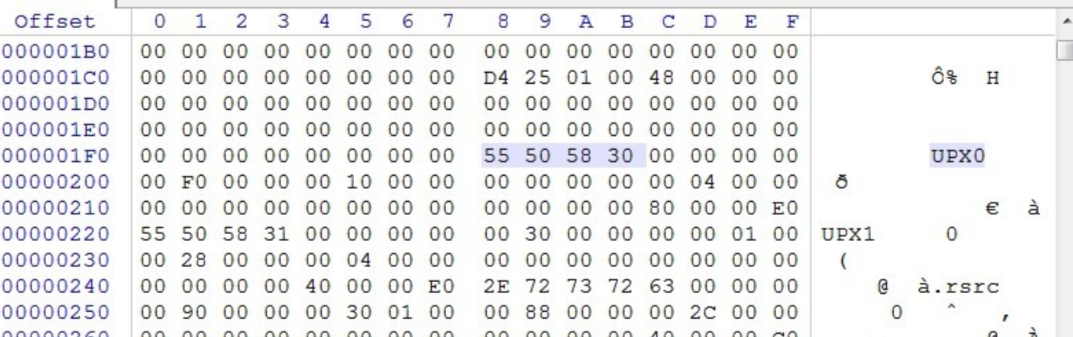
UPX头是供UPX通过“upx-d”命令脱壳用的,并不影响程序运行,可以把它权改为0,或者其他的数,这样就无法使用upx -d命令来快速脱壳
其实 exeinfope上显示了被修改了的upx特征,只要把它改回upx即可


改成这样了
然后保存
继续脱壳

然后用ida打开,我们发现两个函数对输入进行了处理
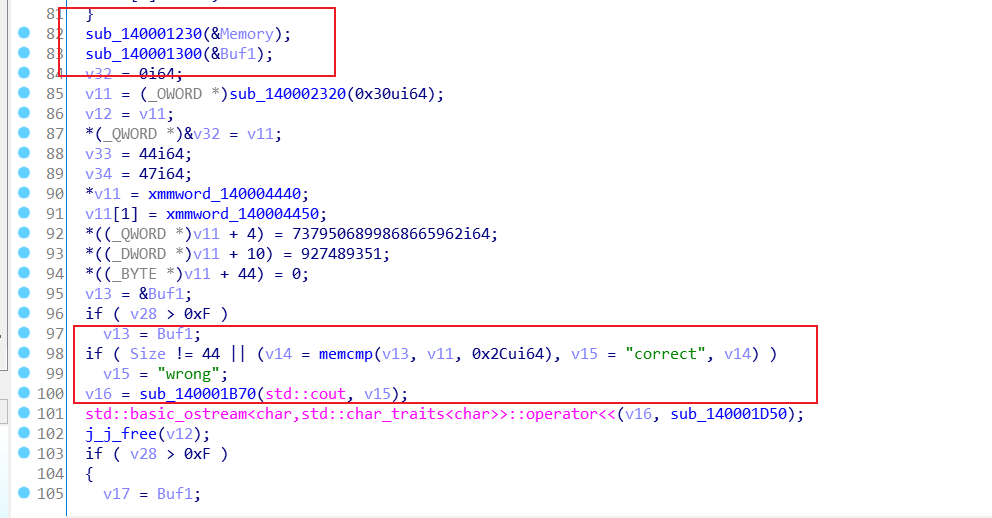
-
对输入进行自定义Base64编码
-
编码结果与硬编码的目标数据比较
我们通过动态调试去完成找到base64的编码和目标数据
先在这里下断点去找到
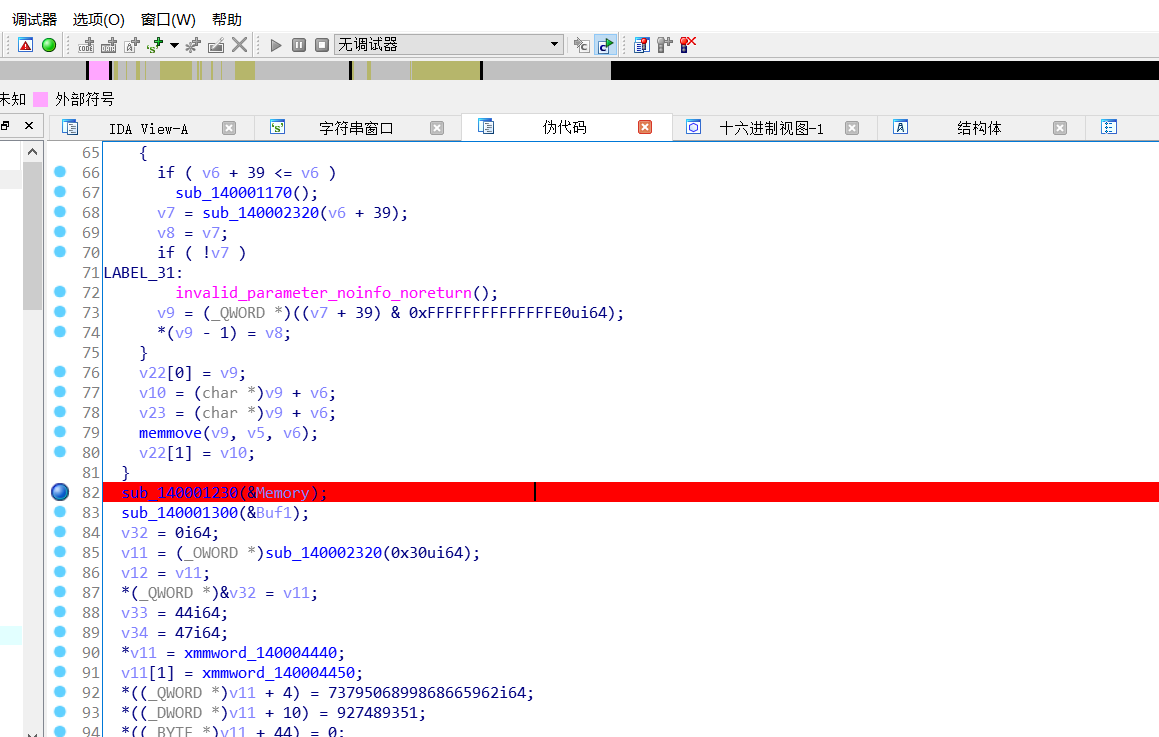
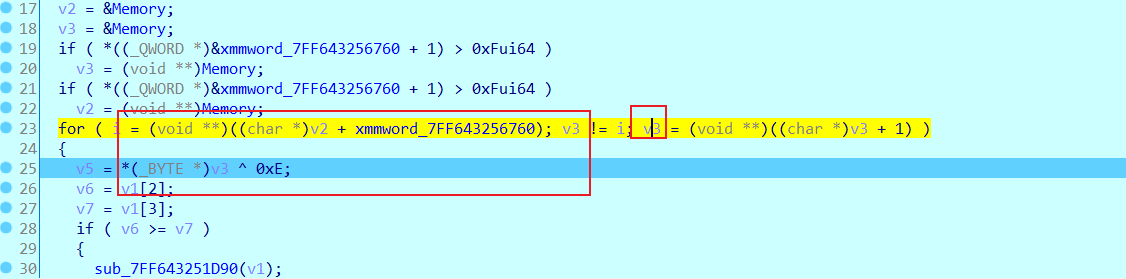
我们查看v3发现是我们的数据base64编码

然后进行异或操作
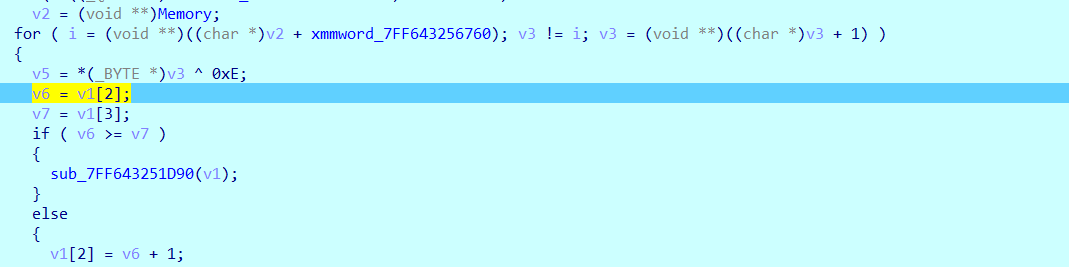
然后再对比较函数这里打一个断点
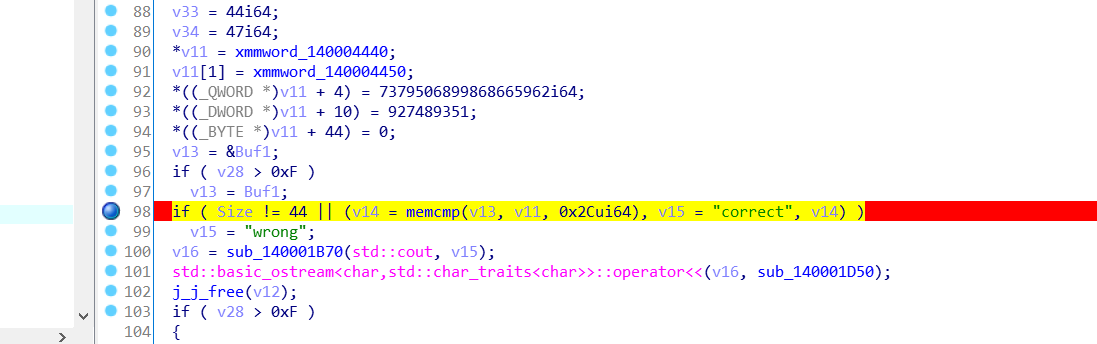
可以看到

然后进行解密
import base64# 你找到的原始编码表数据(64字节)
original_table = bytes([0x41, 0x42, 0x43, 0x44, 0x45, 0x46, 0x47, 0x48, 0x49, 0x4A, 0x4B, 0x4C, 0x4D, 0x4E, 0x4F, 0x50,0x51, 0x52, 0x53, 0x54, 0x55, 0x56, 0x57, 0x58, 0x59, 0x5A, 0x61, 0x62, 0x63, 0x64, 0x65, 0x66,0x67, 0x68, 0x69, 0x6A, 0x6B, 0x6C, 0x6D, 0x6E, 0x6F, 0x70, 0x71, 0x72, 0x73, 0x74, 0x75, 0x76,0x77, 0x78, 0x79, 0x7A, 0x30, 0x31, 0x32, 0x33, 0x34, 0x35, 0x36, 0x37, 0x38, 0x39, 0x2B, 0x2F
])print("原始编码表:", original_table.decode('ascii'))# 计算实际编码表(每个字节异或0x0E)
custom_table = bytes([b ^ 0x0E for b in original_table])
print("自定义编码表:", custom_table.decode('ascii'))# v11 目标数据(44字节)
v11 = bytes.fromhex('6C593762573D5C636B3F65796A58375D545A5C7D435662685C744F795448363E6A4837586D466966475D4837')# 自定义Base64解码函数
def custom_b64decode(data, custom_table):standard_table = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"translation = str.maketrans(custom_table.decode('ascii'), standard_table)translated = data.decode('ascii').translate(translation)return base64.b64decode(translated)# 解码得到flag
try:flag = custom_b64decode(v11, custom_table)print("Flag:", flag.decode('ascii'))
except Exception as e:print("解码错误:", e)# 尝试直接显示解码结果decoded = custom_b64decode(v11, custom_table)print("原始字节:", decoded)print("十六进制:", decoded.hex())
moectf{Y0u_Re4l1y_G00d_4t_Upx!!!}
guess
“欢迎语 → 生成 0-99 随机数 → 给你 10 次机会猜 → 无论对错都先 RC4 解密硬编码密文 → 只有猜中才把解密结果打印成 flag”
Can you guess my secret number?
打开iida找到main函数发现
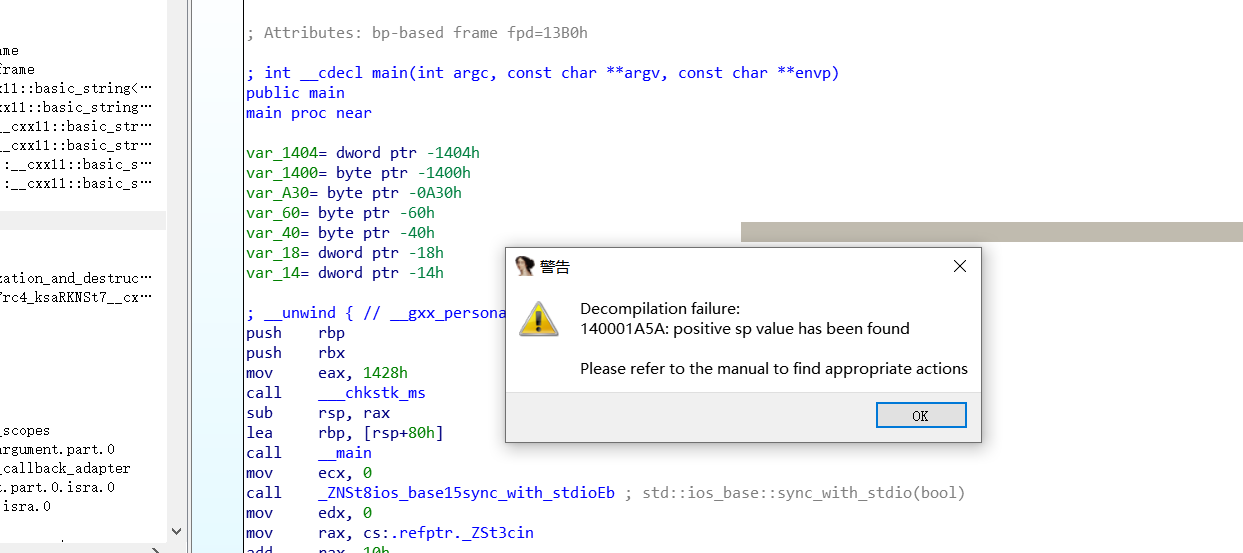
Decompilation failure:
140001A5A: positive sp value has been found“反编译失败:在地址 140001A5A 处发现了 正的栈指针值(positive sp value)。”
按G输入140001A5A 找到这个地方

call loc+3 会多压 8 字节返回地址,IDA 算栈时多减 8,于是 SP 漂移成正值;改成 jmp 后不再压栈,栈指针恢复线性,IDA 就能正确反编译。
我们把这个改为
jmp loc_140001A5F
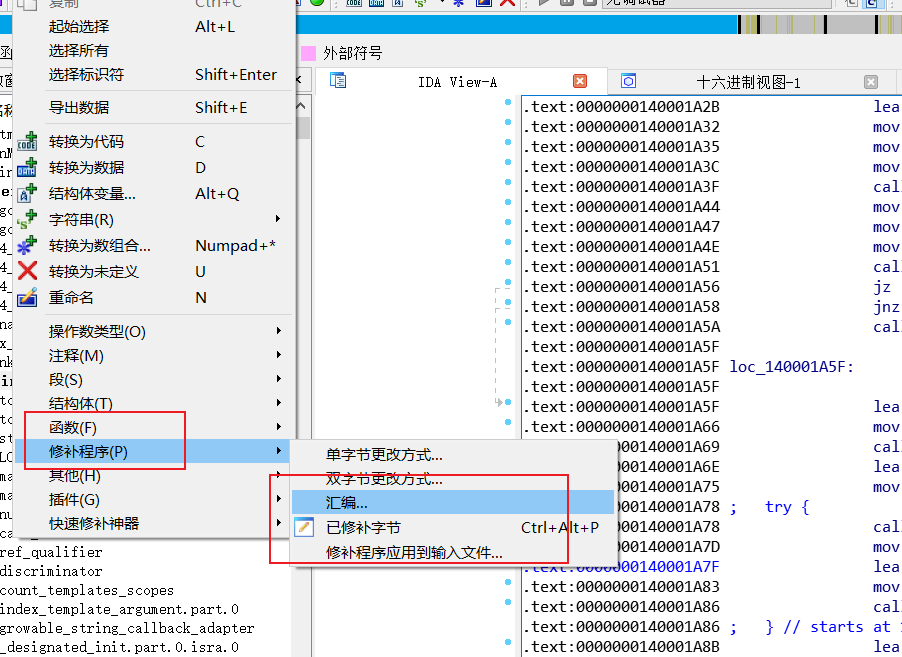

然后保存我们发现可以反编译了

输入为v16 ,随机数为v19所以我们可以动态调试,我们只需要先知道v19的数值然后填写
F8一直过就行了
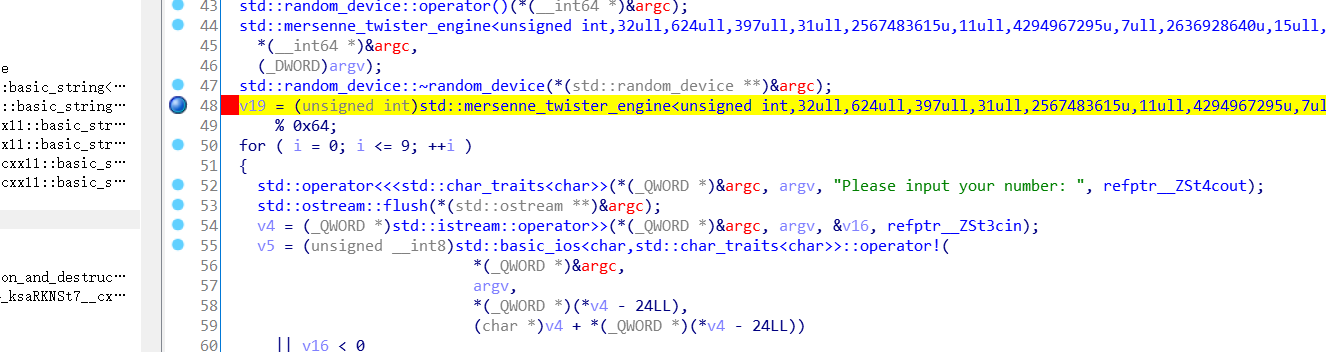
开始调试查看v19的值是40h则为10进制64

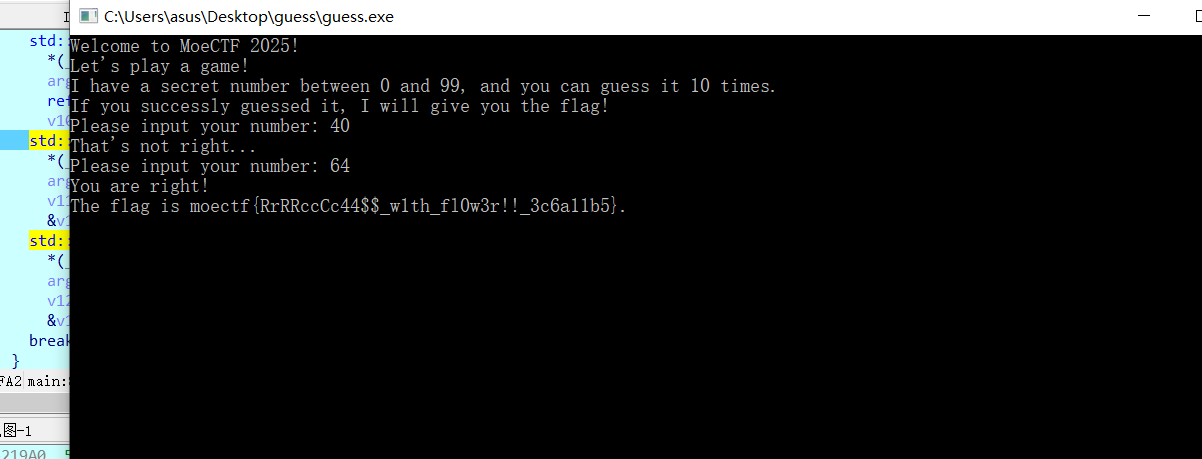
The flag is moectf{RrRRccCc44$$_w1th_fl0w3r!!_3c6a11b5}.
rusty_sudoku

我们只需要破解这个就行了
.rdata:00000001400C2228 a68718379181594 db '.6..8..7.18.3......7.9....1...8...15.9..4.2..54...2..9.....3948..'
.rdata:00000001400C2228 ; DATA XREF: rusty_sudoku::main::hb75a6deccc5f5449+484↑o
.rdata:00000001400C2228 db '...5..7..3....5.You should not change the board!Welcome to MoeCTF'
.rdata:00000001400C2228 db ' 2025!',0Ah
.rdata:00000001400C2228 db 'Please **find** my sudoku and fill it correctly.',0Ah
.rdata:00000001400C2228 db 'And then I will give you the flag.',0Ah
.rdata:00000001400C2228 db 'Input your answer in one line (without spaces).',0Ah
.rdata:00000001400C2228 db 'for example, 8542197633978654212614739857851263946495381721329478'
.rdata:00000001400C2228 db '56926384517513792648478651239 represents:',0Ah
.rdata:00000001400C2228 db '854|219|763',0Ah
.rdata:00000001400C2228 db '397|865|421',0Ah
.rdata:00000001400C2228 db '261|473|985',0Ah
.rdata:00000001400C2228 db '-----------',0Ah
.rdata:00000001400C2228 db '785|126|394',0Ah
.rdata:00000001400C2228 db '649|538|172',0Ah
.rdata:00000001400C2228 db '132|947|856',0Ah
.rdata:00000001400C2228 db '-----------',0Ah
.6..8..7.18.3......7.9....1...8...15.9..4.2..54...2..9.....3948.....5..7..3....5.
直接放在
https://sudoku.com/sudoku-solver

得到数据
369184572185327694274956831632879415897541263541632789756213948918465327423798156
直接运行
moectf{a8c79927d4e830c3fe52e79f410216a0}
A simple program
程序是32位的
打开发现字符串
明显是骗人的
我们先进去看看
明显是骗人的
发现有两个调用的地方
点上去查找函数
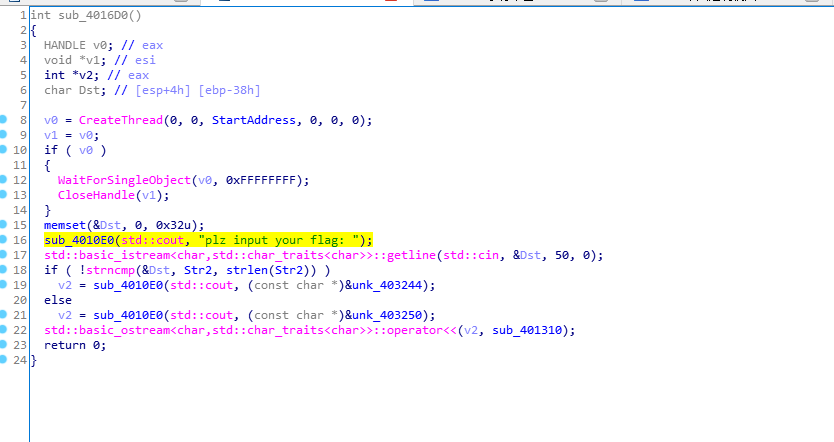
int __cdecl sub_401510(const char *a1, char *a2)
{const char *v3; // ecxunsigned int v4; // edxif ( a2 != Str2 )return dword_4050A0();v3 = a1;if ( strlen(a1) == 20 ){v4 = 0;while ( *v3 == (v3[byte_4031A4 - a1] ^ 0x23) ){++v4;++v3;if ( v4 >= 0x14 )return 0;}}return 1;
}
发现函数,然后去找数据进行解密
.rdata:004031A0 db 0
.rdata:004031A1 db 0
.rdata:004031A2 db 0
.rdata:004031A3 db 0
.rdata:004031A4 ; _BYTE byte_4031A4[24]
.rdata:004031A4 byte_4031A4 db 4Eh, 4Ch, 46h, 40h, 57h, 45h, 58h, 7Ah, 13h, 56h, 7Ch
.rdata:004031A4 ; DATA XREF: sub_401510+31↑o
.rdata:004031A4 db 73h, 17h, 2 dup(50h), 66h, 47h, 2 dup(2), 5Eh, 4 dup(0)
.rdata:004031BC ; char SubStr[]
然后解密
key = bytes([0x4E, 0x4C, 0x46, 0x40, 0x57, 0x45, 0x58, 0x7A,0x13, 0x56, 0x7C, 0x73, 0x17, 0x50, 0x50, 0x66,0x47, 0x02, 0x02, 0x5E
])flag = bytearray(20)
for i in range(20):flag[i] = key[i] ^ 0x23print(flag.decode()) # 20 字节,无 \0
moectf{Y0u_P4ssEd!!}
ezandroid.pro
我们拿到附件用jadx去打开
然后找到主函数
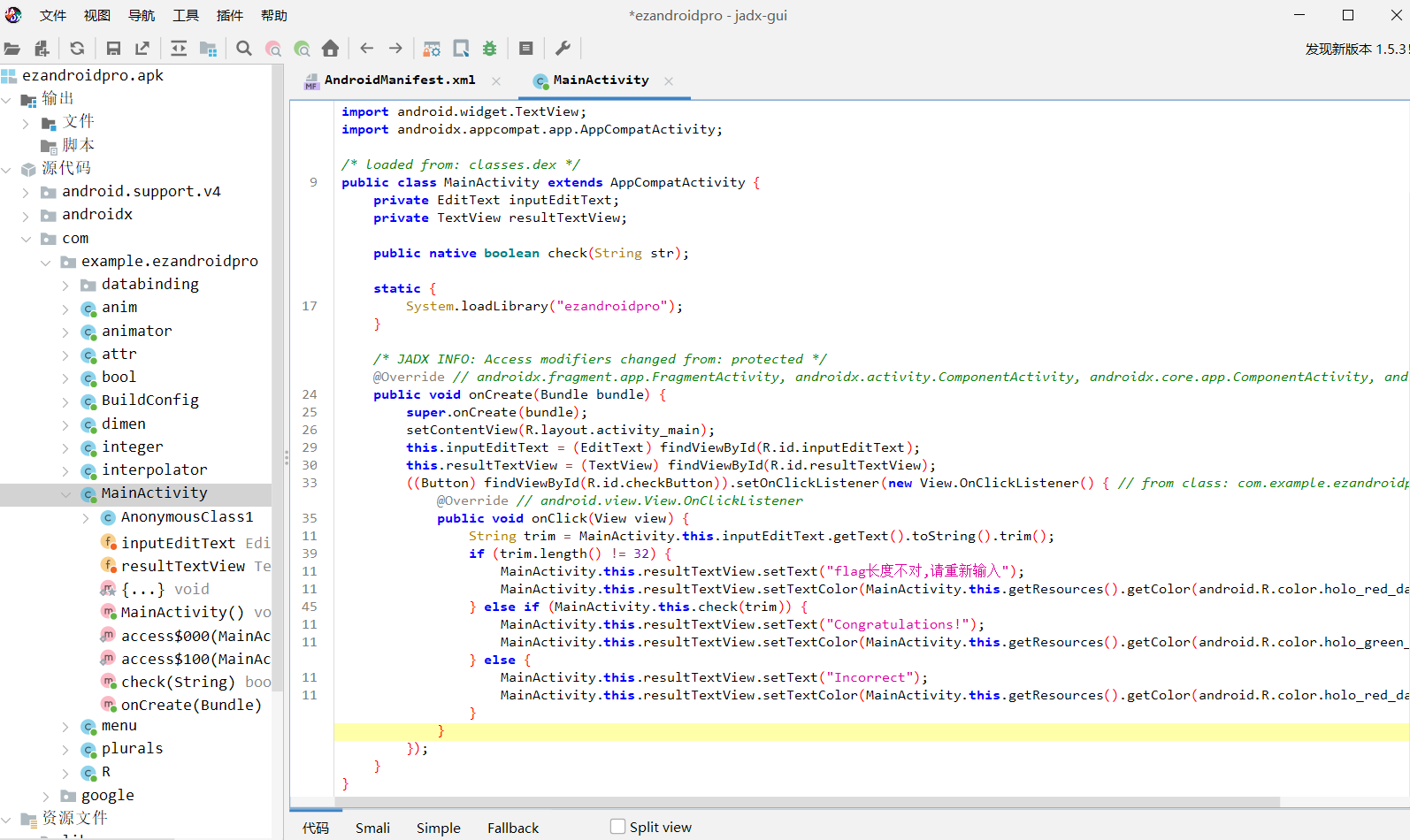
然后我们发现
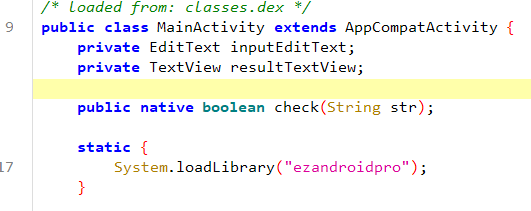
public native boolean check(String str);
所以我们应该要去找
native关键字 = 实现不在 Java 层,而在.so里。
静态块又显式加载了 libezandroidpro.so
static {System.loadLibrary("ezandroidpro");
}
- Java 层只做 长度校验(32 字符) 和 结果提示,真正的判断逻辑 100% 在 native 的
check函数里。
因此:
任何输入想返回 true,都得让 libezandroidpro.so 里的 Java_com_example_ezandroidpro_MainActivity_check 返回 1 → 必须去逆向 / hook /
然后找到apk,把他改为zip文件压缩
在lib目录下发现so文件
然后拖入ida里面分析
- 打开 Exports 窗口 → 搜
check
看到Java_com_example_ezandroidpro_MainActivity_check双击进去

sm4Encrypt
- 密钥在栈上:
v23 = "moectf2025!!!!!!";→ 16 字节 - 密文在
.rodata:
"4EEB1EEF29...7A6AC0B"→ 96 字节 hex(对应 48 字节二进制) - IDA 里按
g跳地址 →Shift+E导出 C array,或者直接复制字符串。
然后丢进在线网站进行解密
在线SM4国密加密/解密—LZL在线工具
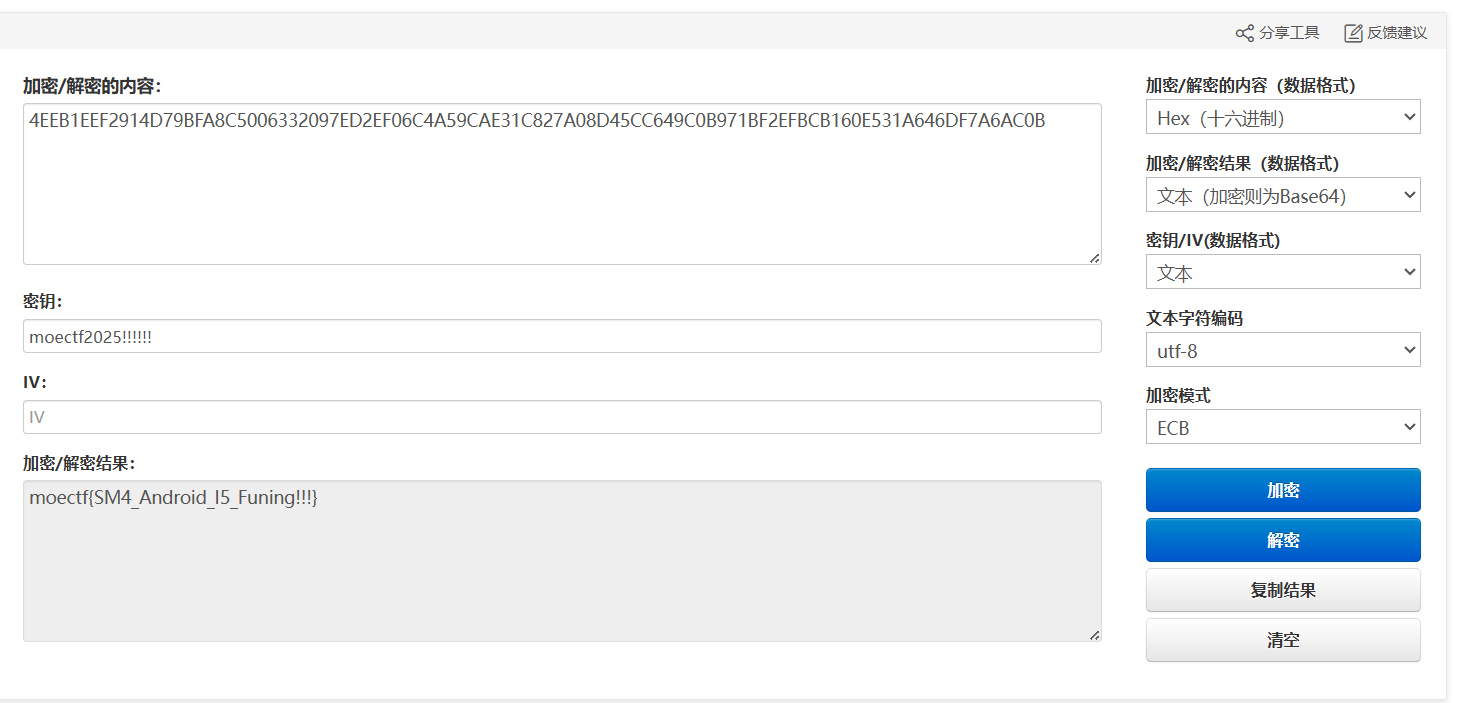
moectf{SM4_Android_I5_Funing!!!}
2048_master_re
打开发现是一个2048小游戏
要达到多少才能拿到flag
玩完之后胡会有一个layout.dat的数据
我们尝试修改1改为99999
保存然后进行玩一下就能得到flag
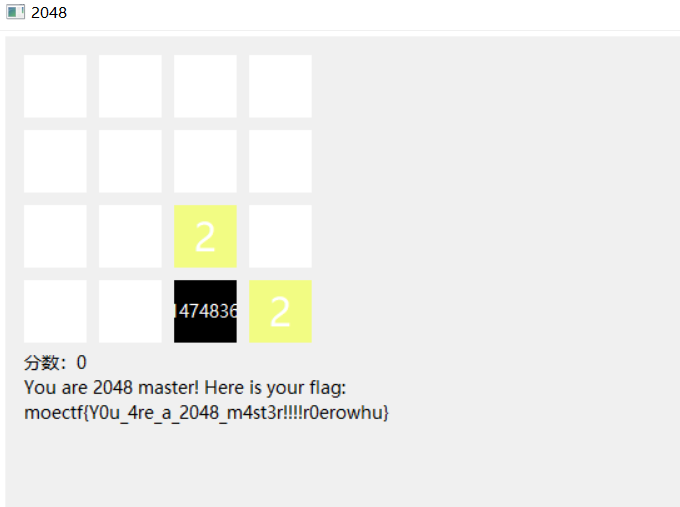
moectf{y0u_4re_a_2048_m4st3r!!!!r0erowhu}
Two cups of tea

发现是64位的进程丢进64位ida里面分析
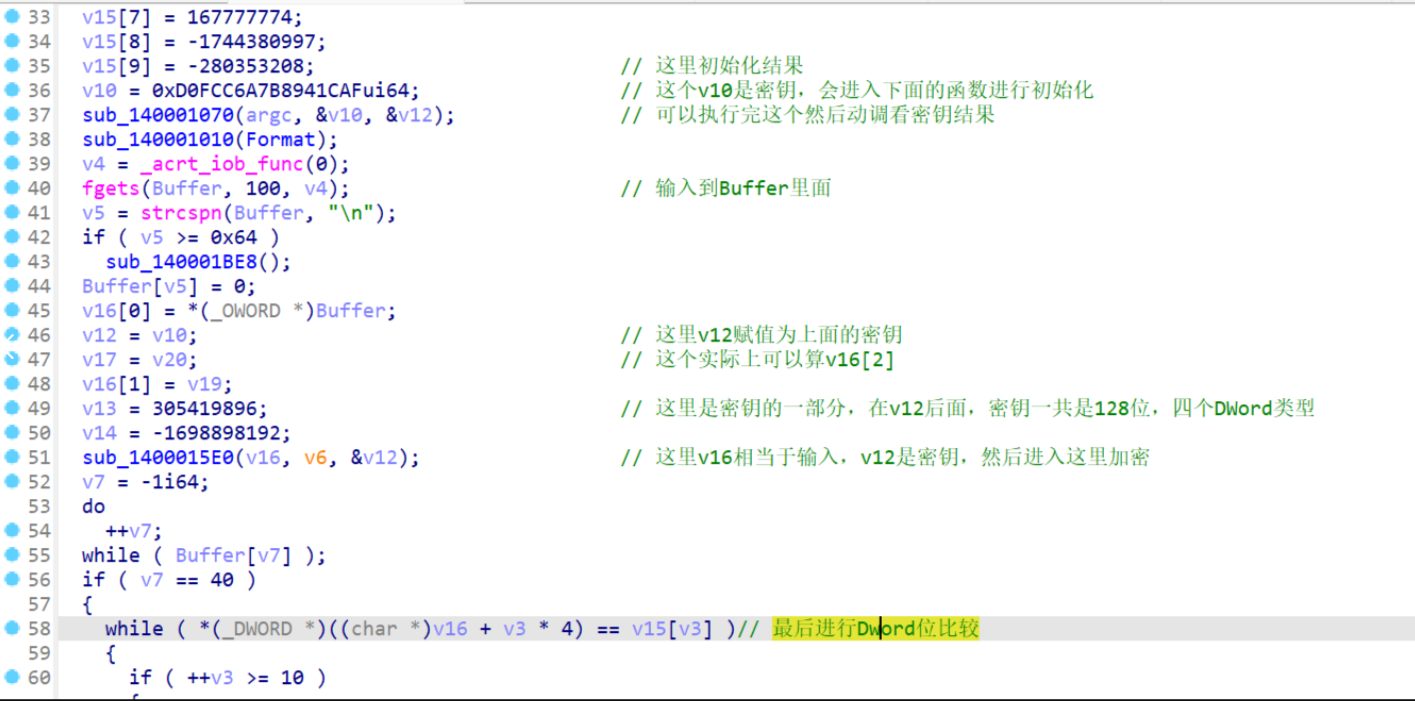
程序的逻辑很简单,首先就是初始化结果,然后对密钥进行初始化,这里37行这个函数可以不看,里面逻辑比较复杂,接着45行将输入赋值到v16里面,然后51行进行加密,最后加密结果与58行进行比较。
这里直接开始动调了,避免重复贴图片,首先我在37行下了一个断点,主要是看v10(密钥)前后的结果,然后再51行下了一个断点就开始调试了

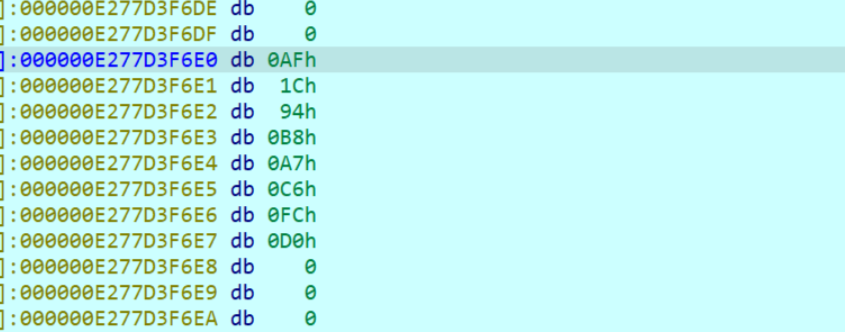
接着我们运行完这个代码然后看结果,实际上可以直接F9运行到我们下一个断点的位置,这里我就F9直接运行了,然后会让你输入

随便输入了一点东西,然后回车就到了第二个断点的位置

但是实际上密钥都是Dword类型使用的,所以这里可以按d改类型,改好了是这样的
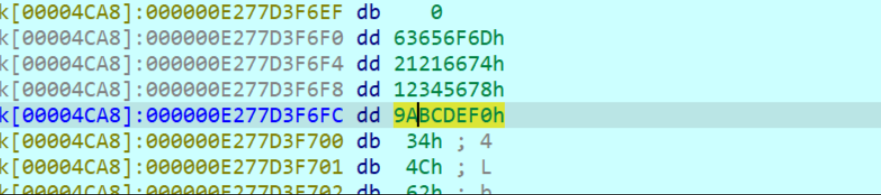
这个12345678,9ABCDEF0是v13,v14的值,实际上也是密钥,这里四个密钥就可以提取了
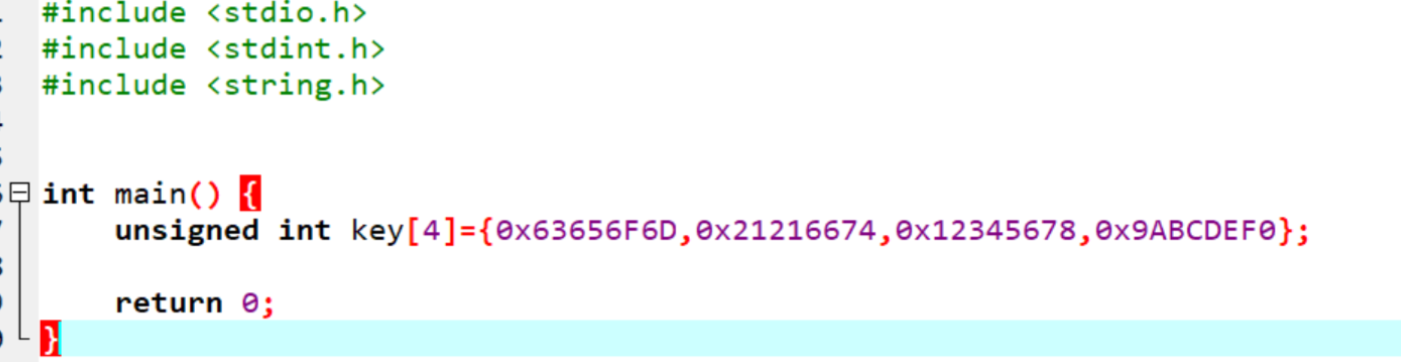
这里由于是tea算法,所以一般优先考虑用c来写,接着我们直接进入这个加密函数,F7单步进入

进来可以按n改一下参数名称
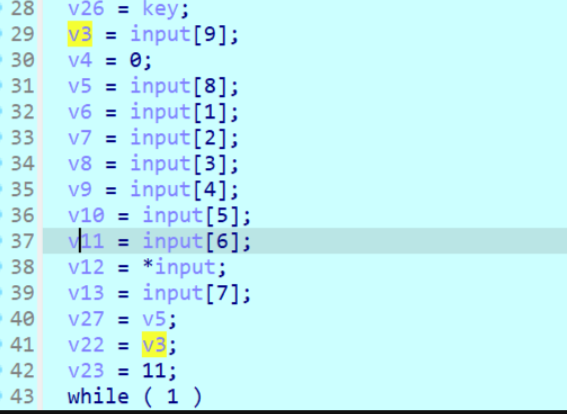
一开始就是一个赋值,这里是这些参数代替我们的输入直接去加密,所以看起来就不是那么清晰,这里建议是键input[i]对应的变量改成input_i.



整体逻辑上就是从input[0]开始加上一个结果,一直加到最后一轮,然后最后得到10个结果。逆向还原肯定就是减去了,但是要注意顺序需要反过来,

#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>int main(void)
{unsigned int a1[10]={1566723124,-2044068179,-1659816037,-53136879,1175413710,-981373336,-28114771,167777774,-1744380997,-280353208};unsigned int key[4]={0x63656F6D, 0x21216674, 0x12345678, 0x9ABCDEF0};int delta=-1640531527*11; unsigned int v16,v18,v26; uint32_t key0,key1,key2;for(int i=0;i<11;i++){v16 = (delta >> 2) & 3 ^ 3;key0=*(key + ((delta >> 2) & 3));key1=*(key + ((delta >> 2) & 3 ^ 1));key2= *(key + ((delta >> 2) & 3 ^ 2));a1[9] -= (((a1[8] ^ key1) + (delta ^ a1[0])) ^ (((16 * a1[8]) ^ (a1[0] >> 3))+ ((a1[8] >> 5) ^ (4 * a1[0]))));a1[8] -= ((a1[7] ^ key0) + (delta ^ a1[9])) ^ (((16 * a1[7]) ^ (a1[9] >> 3))+ ((a1[7] >> 5) ^ (4 * a1[9]))); a1[7] -= ((a1[6] ^ *(key +v16)) + (delta ^ a1[8])) ^ (((16 * a1[6]) ^ (a1[8] >> 3))+ ((a1[6] >> 5) ^ (4 * a1[8])));v18 = (a1[5] ^ key2) + (delta ^ a1[7]);a1[6] -= v18 ^ (((16 * a1[5]) ^ (a1[7] >> 3)) + ((a1[5] >> 5) ^ (4 * a1[7])));a1[5] -= ((a1[4] ^ key1) + (delta ^ a1[6])) ^ (((16 * a1[4]) ^ (a1[6] >> 3))+ ((a1[4] >> 5) ^ (4 * a1[6]))); a1[4] -= ((a1[3] ^ key0) + (delta ^ a1[5])) ^ (((16 * a1[3]) ^ (a1[5] >> 3))+ ((a1[3] >> 5) ^ (4 * a1[5])));a1[3] -= ((delta ^ a1[4]) + (a1[2] ^ *(key + v16))) ^ (((16 * a1[2]) ^ (a1[4] >> 3))+ ((a1[2] >> 5) ^ (4 * a1[4])));a1[2] -= ((a1[1] ^ key2) + (delta ^ a1[3])) ^ (((16 * a1[1]) ^ (a1[3] >> 3))+ ((a1[1] >> 5) ^ (4 * a1[3])));a1[1] -= ((a1[0] ^ key1) + (delta ^ a1[2])) ^ (((16 * a1[0]) ^ (a1[2] >> 3))+ ((a1[0] >> 5) ^ (4 * a1[2])));a1[0]-=((((16 * a1[9]) ^ (a1[1] >> 3)) + ((a1[9] >> 5) ^ (4 * a1[1]))) ^ ((delta ^ a1[1])+ (key0 ^ a1[9])));delta+=1640531527; }for(int i=0;i<10;i++){printf("%c%c%c%c",a1[i]&0xff,(a1[i]>>8)&0xff,(a1[i]>>16)&0xff,(a1[i]>>24)&0xff);}return 0;
}

moectf{X7e4_And_xx7EA_I5_BeautifuL!!!!!}
