这篇文章,带你一次性回顾中学时代里的那些函数。如果对初中、高中的函数还记忆模糊,建议往下翻一翻。
- 一、函数的意义
- 要素
- 特征
- 二、初阶函数
- 1. 一次函数
- 函数特征
- 应用示例
- 2. 反比例函数
- 函数特征
- 应用示例
- 3. 二次函数
- 函数特征
- 应用示例
- 1. 一次函数
- 三、高阶函数
- 4. 指数函数
- 函数特征
- 应用示例
- 5. 对数函数
- 函数特征
- 应用示例
- 6. 幂函数
- 函数特征
- 应用示例
- 7. 绝对函数
- 函数特征
- 应用示例
- 8. Sigmoid函数
- 函数特征
- 应用示例
- 9. 三角函数
- 函数特征
- 应用示例
- 4. 指数函数
- 小结
一、函数的意义
如果说,学数学的核心就在于学习函数,应该没有人会不同意吧。

数学应用的目的是求解现实中的各种问题,其中,为了模拟这种 "已知 xxx, 那么xxx" 论述的过程,函数是最重要的形式。通俗点说,函数就像一个“机器”:你输入一个值,它按照规则处理后输出一个结果
函数的定义通常记为:
其中,x 叫自变量,y 是因变量,大致的意思就是 y 随着 x 的变化而变化,或者说 y 的取值和 x 离不开干系。
那么 f(x) 描述的就是这种关系本身,即通过 x 要怎样推断出 y 的值。
要素
严格说,函数包含三个要素,如下面的示例函数:
- 要素1, 定义域, x 的取值范围,如 \(x \in \mathbb{R}\)
- 要素2, 值域,y 也就是 f(x) 的结果取值范围, 如 \(y \in \mathbb{R}\)
- 要素3, 计算法则,即 f(x) 公式本身
特征
既然函数描述了数据之间的关系,而现实场景中数据的关系会存在一些规律,这些规律通过图像特征也能够直观的看出。一些常见的规律就包括:
单调性
函数单调性描述的是函数值随着自变量的变大是变大还是变小,如单调递增或递减。
举例:我们的愿望是,👉 工资和自己工作年限的关系是单调递增,工作越久,工资越高。
奇偶性
奇偶性描述的是函数在正负方向上的对称性,例如当x为2和-2时,y=4则为偶函数,若y=4和-4则为奇函数
举例:我是一面镜子,也是一个偶函数。
对称性
函数图像是否在某个轴或点上呈现对称结构,可以认为奇偶性是特殊的对称性。
举例:蝴蝶的翅膀是左右对称的。
周期性
周期性表示函数的图像或数值每隔一段时间,会重复一次
举例:钟表的指针运动、日出日落、心跳波形等等。
二、初阶函数
1. 一次函数
一次函数的公式如下:
- k 是斜率(不能为 0),表示函数的变化速度;
- b 是常数,表示图像在 y 轴上的截距。
当 b = 0 时,函数变为 y = kx,是一个正比例函数。
在几何上,一次函数是一条直线,如下:
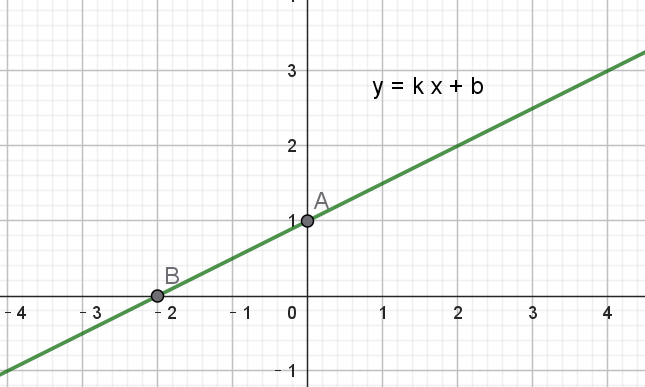
函数特征
| 特征项 | 描述说明 |
|---|---|
| 📍 图像形状 | 一条直线 |
| 📈 斜率 k | 决定直线的倾斜方向和陡峭程度 |
| 📍 截距 b | 决定图像与 y 轴的交点位置 |
| 🔁 单调性 | 当 k>0,函数递增;当 k<0,函数递减 |
| 🧭 象限分布 | 根据 k 和 b 的符号,图像穿过不同象限 |
应用示例
假定你是一家小商店老板,需要做整体成本计算
- 表达式:\(y =5x+100\)
- 含义:x 代表 每件商品成本为 5 元,固定成本为 100 元。
2. 反比例函数
反比例函数的公式如下:
- k 是常数,且 \(x≠0\)
反比例函数的图像是一条双曲线,如下:
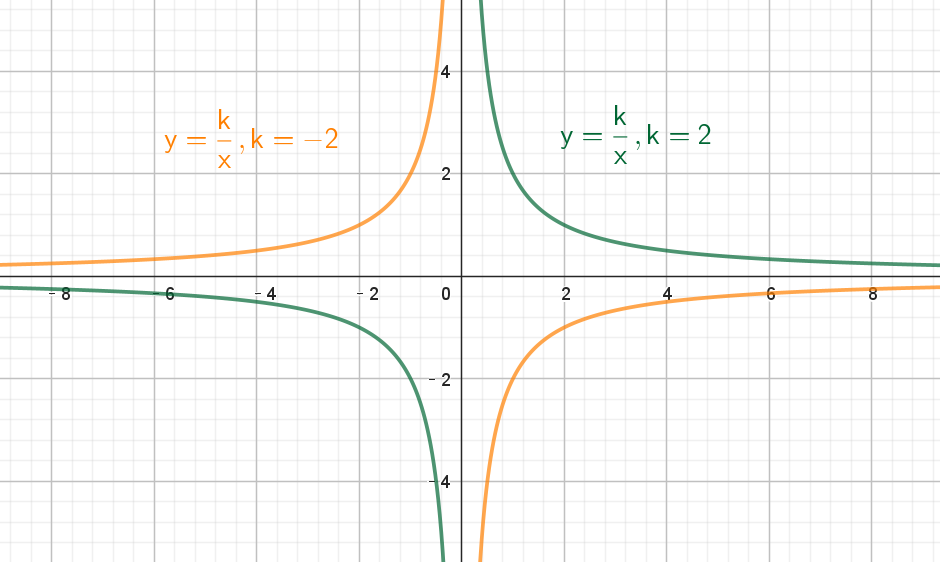
当 k > 0 时,图像位于第一象限和第三象限;
当 k < 0 时,图像位于第二象限和第四象限。
函数特征
| 特征项 | 描述说明 |
|---|---|
| 📍 图像形状 | 双曲线,两支分别位于对角象限 |
| 🔁 单调性 | 在每个象限内单调递减 |
| 🚫 不连续点 | 在 x=0 处无定义,图像断裂 |
| 🧭 对称性 | 关于原点中心对称 |
| 📈 渐近线 | x轴和y轴是渐近线,图像无限接近但不相交 |
应用示例
.工厂作业时,计算工作效率与时间的关系
- 表达式:\(y = \frac{10}{x}\)
- 含义:完成同一任务所需时间 y 与工人数 x 成反比。
- 举例:10人完成任务需1小时,5人则需2小时。
3. 二次函数
二次函数的公式如下:
- \(a \neq 0\),否则退化为一次函数;
- b, c 为常数。
二次函数的图像是一条抛物线,如下:

掌握二次函数需要理解判别式:
判别式的符号与二次函数的图像特征有特定的关系,如下所示:

函数特征
| 特征项 | 描述说明 |
|---|---|
| 📍 图像形状 | 抛物线 |
| 🔁 开口方向 | a > 0 向上开口,a<0 向下开口 |
| 🎯 顶点坐标 | \((-\frac{b}{2a}, \frac{4ac - b^2}{4a})\) |
| 🧭 对称轴 | \(x = -\frac{b}{2a}\) |
| 📈 单调性 | 顶点左侧递减,右侧递增(或相反) |
| 🚫 零点 | 与 x 轴交点由判别式 \(\Delta = b^2 - 4ac\) 决定 |
应用示例
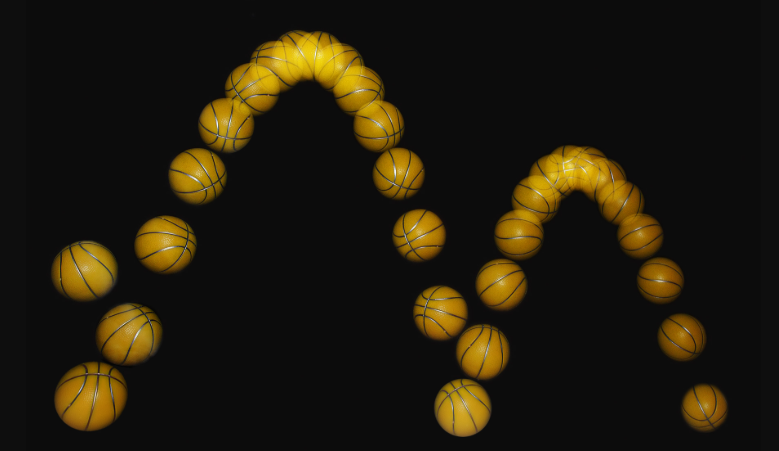
抛体运动高度计算,物体在竖直方向上,高度随时间变化的关系。
-
表达式:\(y = -\frac{1}{2}gt^2 + v_0t + h_0\)
-
含义: g 是重力,v0 是初始速度,h0 是初始高度。
三、高阶函数
4. 指数函数
指数函数的公式如下:
其中:
- a 是底数,必须为正且不等于 1;
- 函数值 y 是底数 a 的 x 次幂。
指数函数的图像是一条光滑曲线,如下:

函数特征
| 条目 | 特征说明 |
|---|---|
| 📈 增减性 | 当 a > 1 时,函数递增;当 0<a<1 时,函数递减 |
| 📍 交点 | 图像恒过点 (0, 1),因为 \(a^0 = 1\) |
| 🚫 渐近线 | x 轴是水平渐近线,图像无限接近但不相交 |
| 🧭 定义域 | \((-\infty, +\infty)\),值域为 \((0, +\infty)\) |
| 🔁 单调性 | 在整个定义域内保持单调性,无极值点 |
应用示例

金融场景下,利用指数函数进行复利计算:
- 表达式:\(A = P(1 + r)^n\)
- 含义:本金 P 在利率 r 下经过 n 期后的总额。
5. 对数函数
对数函数可看作是指数函数的反过程,对数函数的定义如下:
- 底数 a 的多少次幂等于 x,即 \(a^y = x\)
- a是底数,必须为正且不等于 1
- x 是正数,必须大于 0
- y 是以 a 为底的 x 的对数
对数函数的图像是一条光滑曲线,和相应的指数函数沿着 y=x 直线呈对称关系,如下:

函数特征
| 特征项 | 描述说明 |
|---|---|
| 📍 图像形状 | 曲线,呈现递增或递减 |
| 📈 单调性 | 当 a > 1,图像递增;当 0 < a < 1,图像递减 |
| 📍 交点 | 恒过点 (1, 0),因为 \(\log_a 1 = 0\) |
| 🚫 渐近线 | y 轴(即x = 0)是垂直渐近线 |
| 🧭 定义域 | x > 0,值域为 (−∞,+∞) |
应用示例
碳-14测年法(Carbon-14 dating)是一种非常重要的放射性同位素测定技术,可用来估算有机遗骸的年代。
当生物死亡后,它就不再吸收碳,体内的 \(^{14}C\) 开始以固定速率衰减。通过测量遗骸中剩余的 \(^{14}C\) 含量,就可以推算出死亡时间。
- 表达式:\(N=N_0⋅e^{−λt}\),推出 \(t = \frac{1}{\lambda} \log_e \left( \frac{N_0}{N} \right)\)
- 含义: N0 是初始碳-14量值,N 是当前值,λ 衰变常数,e是自然对数。
6. 幂函数
幂函数的公式如下:
- a 是常数(通常为系数);
- n 是幂指数,可以是正数、负数、分数甚至无理数;
- 当 a = 1 时,函数简化为 \(f(x) = x^n\),这是最常见的形式。
从几何上看,幂函数的图像形状随指数 n 的不同而变化显著,如下:

函数特征
| 幂指数 n | 图像特征说明 |
|---|---|
| 正整数(偶数) | 图像关于 y 轴对称,开口向上,如 \(y = x^2\) |
| 正整数(奇数) | 图像关于原点对称,穿过原点,如 \(y = x^3\) |
| 分数指数 | 图像在第一象限,如 \(y = \sqrt{x}\),定义域为 \(x \geq 0\) |
| 负整数 | 图像呈双曲线状,如 \(y = x^{-1}\),在 x = 0 处无定义 |
应用示例
电功率公式:\(P = I^2 R\)
-
含义:其中 I是电流,R 是电阻。
-
说明:该公式基于欧姆定律和功率公式结合得出,用于适用于电阻器、电热器等纯电阻负载的计算。
7. 绝对函数
绝对函数的公式如下:
- ∣x∣表示数 x 到原点的距离;
- 当 \(x \geq 0\),∣x∣=x;
- 当 \(x<0\),|x| = -x。
绝对函数本质上是一个分段函数,在图像上是一条“V” 型折线,如下:

函数特征
| 特征项 | 描述说明 |
|---|---|
| 📍 图像形状 | V 形折线,左右对称 |
| 📈 单调性 | 左侧递减,右侧递增; |
| 📍 交点 | 顶点在原点 (0, 0),是图像的转折点; |
| 🚫 斜率 | 左侧斜率为 -1,右侧斜率为 +1; |
| 🧭 定义域 | 最小值为 0,无最大值。 |
应用示例
在评估传感器数值的准确度时,经常会使用 MAE 方法进行误差分析
- 表达式:\(\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |\text{测量值}_i - \text{真实值}_i|\)
- 含义:将多次历史数据的测量值与真实值之间的误差进行平均计算,得到评估的准确度。
8. Sigmoid函数
Sigmoid 函数(也称为 Logistic 函数)是一种收敛函数,适用于解决概率建模和二分类问题,也是机器学习和深度学习中常见的激活函数。
Sigmoid 函数的定义如下:
- e 是自然常数(约等于 2.718);
- 输出值\(f(x) \in (0, 1)\),即将任意实数压缩到 0 到 1 的区间。
从几何上看,Sigmoid 函数是一个值介于0和1之间的渐进式曲线,如下:
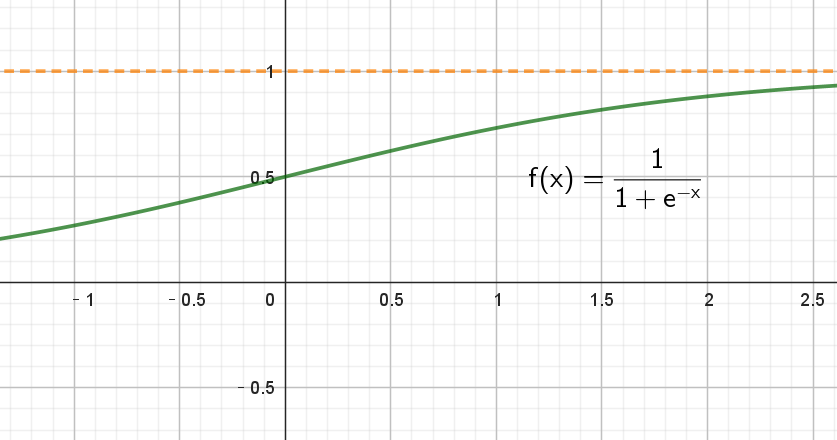
函数特征
| 特征项 | 描述说明 |
|---|---|
| 📈 单调性 | 函数在整个定义域上单调递增 |
| 🎯 对称性 | 图像关于原点对称 \(f(-x) = 1 - f(x)\) |
| 📍 极限值 | 当 \(x \to -\infty,f(x) \to 0\);当 \(x \to +\infty,f(x) \to 1\) |
| 🧭 中心点 | 当 x = 0,f(x)=0.5,图像在此处最陡 |
| 🚫 渐近线 | y 轴两侧分别有水平渐近线 y=0和 y=1 |
应用示例

神经网络激活函数
- 用于隐藏层或输出层,将神经元输出压缩到 (0,1)(0, 1) 区间;
- 举例:在二分类问题中,输出值可解释为属于正类的概率。
9. 三角函数
三角函数是数学中用于描述角与边之间关系的基本函数,广泛应用于几何、物理、工程、天文等领域。
三角函数的公式如下:
| 函数 | 图像形状 | 周期 | 振幅 | 对称性 |
|---|---|---|---|---|
| \(\sin x\) | 波浪形 | \(2\pi\) | 1 | 奇函数,关于原点对称 |
| \(\cos x\) | 波浪形 | \(2\pi\) | 1 | 偶函数,关于 y 轴对称 |
| \(\tan x\) | 间断曲线 | \(\pi\) | 无界 | 奇函数,关于原点对称 |
函数特征

应用示例

物理振动建模,使用正弦波的数学表达式来描述物体振动随时间变化的波动情况。
- 表达式:\(x(t) = A \sin(\omega t + \phi)\)
- 含义:\(\omega 是角频率(波动的快慢),t 是时间,\phi 是初始偏移,A 是振幅\)。
- 举例:\(x(t)=5sin(2πt),振幅为5米,\omega = 2\pi,即频率为 1 Hz(每秒一周期),初始偏移为0\)
小结
函数是中学数学教材的主要学习和考试内容,它同时也有着大量的实际场景应用。在机器学习和深度学习领域,存在不少以函数为基础的理论研究和实践。但不幸的是,对大部分职场老鸟来说,这些内容因时间和职业方向关系早已不再熟悉。本文对早期常见的一些基础函数做了整理,旨在帮助快速回顾并建立一些基础知识印象。

