https://www.bilibili.com/video/BV14P411T7TZ
n个+1 和n个-1的序列问题
这个是本质的模型
折线图证明方法(对称思想值得学习)
括号序列计数问题:
由 n 对括号构成的合法括号序列数为 \(C_n\)


\(n+1\)个数要加 \(n\) 对括号, 左括号视为-1, 右括号视为+1
二叉树计数问题
含有 \(n\) 个非叶结点的形态不同的满二叉树数目为 \(C_n\)。
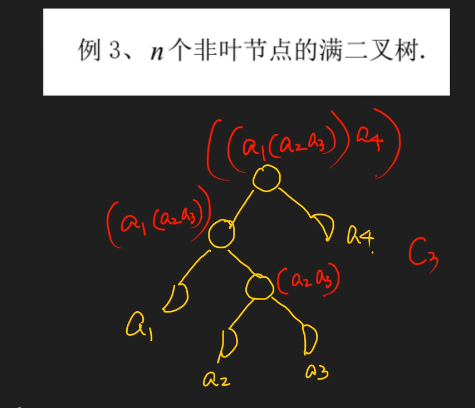
叶子节点对应一个数, 非叶节点相当于把对应的子节点加了一次括号。 这样就转化为加括号问题
三角剖分计数问题:
对角线不相交的情况下,将一个凸 \((n+2)\) 边形区域分成三角形区域的方法数为\(C_n\)


设 \((n+2)\) 边形三角剖分的方案数为\(f(n)\) , 先选定一条边 \((0,n+1)\) 作为基边,它一定属于一个三角形,记该三角形的第三个点为 k, 这样就把多边形剖成2部分。递归计算,k的不同剖法有n种
圆内不相交弦计数问题

也是剖分递归思想。 注意到1号点只能与偶数号点连接。(oiwiki这题讲的不错)
