解决的问题
斜率优化 DP 可以优化以下形式的转移方程:
其中 \(a(i),c(i)\) 表示与 \(i\) 有关的函数,\(X(j),Y(j)\) 表示与 \(j\) 有关的函数,\(L\) 代表一个常量。
在上面的式子中,如果 \(a(i)\times X(j)\) 不存在那么就是单调队列或者线段树优化,其余的东西的存在与否并不重要。
解决办法
考虑如果存在 \(j1,j2\),满足 \(j1<j2\) 且 \(j1\) 劣于 \(j2\)(默认取 \(\min\),也就是 \(F(j1)>F(f2)\),如果是 \(\max\) 反过来就行了)。
就有:
化简得到:
发现上面这个东西和 \(y=kx+b\) 的一次函数很像,那么令 \(k_0=a(i)\) 就有:
移项,然后提取公因式:
不妨设 \(X(j2)>X(j1)\),注意用的时候不等号的方向,那么同除得到:
总结一下,也就是如果上面的式子成立,那么 \(j2\) 比 \(j1\) 优秀。
如果令 \(k_0\gets -k_0\) 那么就和求斜率的式子一模一样了,考虑把 \(X,Y\) 搬到直角坐标系里。
下面只考虑不等式是 \(>\) 的情况。
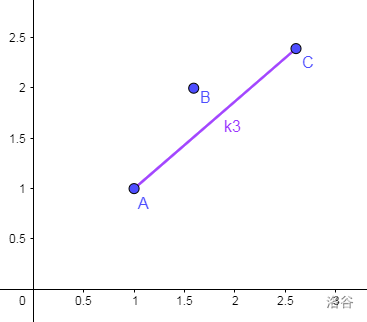
假设三个决策点分别是 \(A,B,C\),\(AB\) 的斜率是 \(k1\),\(BC\) 的斜率是 \(k2\)。
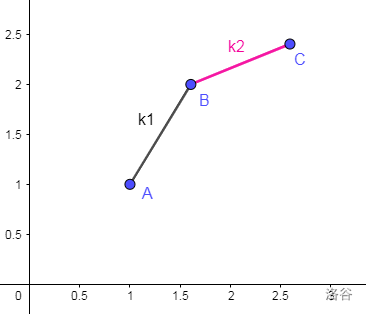
- 如果 \(k_0>k_1\),那么 \(B\) 比 \(A\) 优。
- 如果 \(k_0>k_2\),那么 \(C\) 比 \(B\) 优。
- 显然根据图像有 \(k1>k2\),也就是 \(B\) 是一个上凸。
有三种情况:
- \(k_0>k_1\wedge k_0>k_2\),那么 \(C\) 优于 \(B,A\)。
- \(k_1>k_0\wedge k_0>k_2\),那么 \(A,C\) 优于 \(B\)。
- \(k_1>k_0\wedge k_2>k_0\),那么 \(A\) 优于 \(B,C\)。
根据上面的分析,得到结论上凸永远都不可能是最优点。
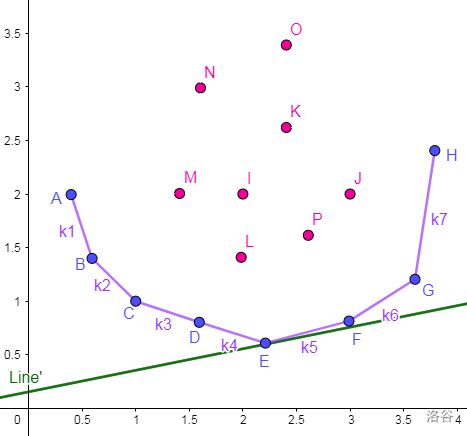
把上凸全部删除之后得到的肯定是一个下凸,也就是这样的东西:

假设下图中的红线是 \(k_0\),那么肉眼可与看出第 \(5\) 个决策点是最优秀的。
因为 \(5\) 要节点之后的 \(k\) 都大于 \(k_0\),前面的都小于 \(k_0\)。
所以说 \(5\) 就是第 \(1\) 个比 \(k_0\) 的斜率大的连线的靠前的决策点。
发现因为是下凸,所以有单调性可以二分。
如果有 \(m\) 个决策点,那么这样二分:
double slope(int i,int j){if(X(j)==X(i)) return Y(j)>=Y(i)?inf:-inf;return 1.0*(Y(j)-Y(i))/(X(j)-X(i));
}
int F(int k0){int l=1,r=top-1,p=inf;while(l<=r){int mid=(l+r)/2;if(slope(mid,mid+1)<k0) l=mid+1,p=mid;else r=mid-1;}if(p==inf) return s[1];return s[p+1];
}
总结
如果是(取 \(\min\) 且 \(X\) 单调递增)或者(取 \(\max\) 且 \(X\) 单调递减)那么维护下凸。
否则,维护上凸。
注意事项
- 尽量避免使用除法,避免精度误差。
- 注意一些情况需要向凸包内加入如 \(\{0,0\}\) 这样的初始值。
- 注意可能 \(X\) 的值一样,需要加一个 \(mdf\) 来扰动以下。
- 在把式子整理的时候 \(c(i)+L\) 其实就是和 \(j\) 无关的东西,不一定要分开。
- 注意是否要保留这样的斜率一样的情况:
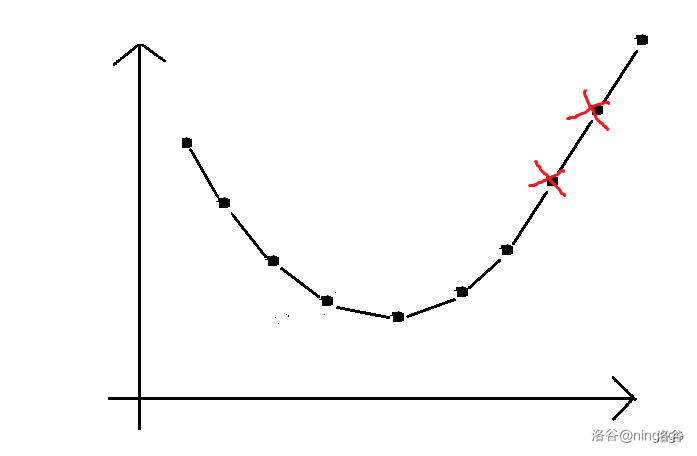
补充
对于 \(X\) 不单调的情况,我们就不能进行直接移项,考虑进行一些奇技淫巧进行调整。
我们考虑分治,先处理左区间,然后再用左区间得到的结果处理右区间。
具体的,把左右区间分别递归完之后再归并排序即可。
整体来说就是一个 CDQ 分治,另外也可以使用李超线段树。
