前言
请怀着批判性思维阅读,如果有任何问题欢迎前来踩爆我。
群
定义
如果一个集合 \(S\ne \varnothing\),且在 \(S\) 上的运算 \(\cdot\) 满足一下要求,得到我们称 \((S,\cdot)\) 为一个群。
- 封闭性:\(\forall a,b\in S\),\(a\cdot b\in S\)。
- 结合律:\(\forall a,b,c\in S\),\((a\cdot b)\cdot c=a\cdot(b\cdot c)\)。
- 单位元:\(\exists e\in S\),\(\forall a\in S\),\(a\cdot e=a\)。
- 逆元:\(\forall a\in S\),\(\exists inv\in S\),\(a\cdot inv=e\)。
子群
如果群 \(G(S,\cdot)\) 满足 \(H(T,\cdot)\) 也是一个群且 \(T\subseteq S\),那么我们称 \(H\) 是 \(G\) 的一个子群,记作 \(H\le G\)。
简单性质
单位元唯一
对于一个群 \((S,\cdot)\),其单位元 \(e\) 是唯一的。
假设群中有两个不同单位元 \(e_1,e_2\),那么就有 \(e_1=e_1\cdot e_2=e_2\),与假设矛盾,故只有一个单位元。
逆元不分左右
对于一个群 \((S,\cdot)\),如果 \(a\cdot x=e\),那么 \(x\cdot a=e\)。
不妨设 \(c\cdot a=e\),那么 \(x\cdot a=(c\cdot a)\cdot (x\cdot a)=c\cdot a\cdot(a\cdot x)=c\cdot a=e\)。
逆元唯一
对于一个群 \((S,\cdot)\) 中的任意元素 \(x\),其逆元 \(inv\) 是唯一的。
假设存在 \(x\) 的两个逆元 \(inv_1,inv_2\),那么满足 \(inv_1=inv_1\cdot x\cdot inv_2=inv_2\)。
置换
定义
一个序列(有序且不可重复的)自身的一种双射被称为置换,对于 \(S=\{a_1,a_2,\cdots,a_n\}\) 的置换可以写作:
表示把第 \(i\) 个位置的元素换到第 \(p_i\) 个位置。
其实实际上置换更改的是下标还是具体的值在这篇文章中都是不影响的,因为在所有实际应用中的序列中的元素都满足 \(a_i=i\)。
乘法
对于两个置换:
那么两个置换相乘的结果为:
置换群
对于一个集合 \(S\) 的所有置换与置换乘法在一起满足封闭性、结合律、有单位元、有逆元,因此它们构成了一个群。
通常我们把 \(\{1,2,\cdots,n\}\) 构成的置换与置换乘法组成的记作 \(S_n\)。
对于 \(S_n\) 的任意子群,我们称之为置换群。
循环置换
对于这样的特殊的置换,我们称之为循环置换。
对于循环置换可以简记为:
需要注意,下面的置换也是循环置换。
置换的性质
如果两个置换不包含相同的元素,那么我们称两个置换是不相交的。
那么有性质,对于所有的置换都可以通过若干个不相交的循环乘积,例如:
如果把元素视为图的节点,映射关系视为有向边,则每个节点的入度和出度都为 \(1\)。
因此形成的图形必定是若干个环的集合,而一个环即可用一个循环置换表示。
我们定义如果一个置换至少通过 \(x\) 个不相交的循环置换表示,那么我们成这个置换的阶为 \(x\)。
不动点
如果序列中的一个元素 \(s\) 所在的序列经过一个置换操作 \(p\) 之后 \(s\) 的位置没有变化,那么我们称 \(s\) 是 \(p\) 操作的不动点。
定义 \(c(p)\) 表示置换 \(p\) 的不动点个数。
\(k\) 不动置换类
设 \(G\) 是 \([1,n]\) 的一个置换群,\(k\in[1,n]\)。那么在 \(G\) 中所有的置换中能让元素 \(k\) 保持不变的全体置换构成的集合被称为 \(k\) 不动置换类,记作 \(Z_k\)。
一个性质
\(k\) 不动置换类肯定是 \(G\) 的子群。
封闭性:因为所有让 \(k\) 不变的都在里面,所以具有封闭性。
结合律:因为 \(\circ\) 本身就具有结合律,所以显然满足。
单位元:因为单位元不会造成变化,所以肯定在 \(Z_k\) 中。
逆元:因为 \(p\) 的逆元 \(p^{-1}\) 也不会让 \(k\) 变化,所以也在 \(Z_k\) 中。
等价类
对于元素 \(k\) 施加任意的 \(G\) 中的置换,最终可以得到的所有的元素构成的集合就是 \(k\) 的等价类,记作 \(E_k\),有称为轨迹。
例如 \(G=\{(1,2),(2,3),(1,3),e,(4,5),(4,5,6)\}\),那么 \(E_1=\{1,2,3\}\)。
一个性质
当 \(x,y\) 属于一个等价类时,\(\lvert Z_x\rvert =\lvert Z_y\rvert\)。
考虑构造 \(Z_x\) 到 \(Z_y\) 之间的双射,如果构造出来那么就肯定满足 \(\lvert Z_x\rvert=\lvert Z_y\rvert\)。
根据等价类的定义,\(\exists t\in G\) 满足 \(x \xrightarrow{t}y\) 且 \(y\xrightarrow{t^{-1}}x\)。
那么对于任意的 \(p\in Z_x\) 都有 \(y\xrightarrow{t^{-1}}x\xrightarrow{p}x\xrightarrow{t}y\),那么构造 \(p'=t^{-1}pt\),则必有 \(p'\in Z_y\)。
于是就构造出了一组二者之间的双射。
\(k\) 不动置换类-等价类(轨道-稳定子)定理
设 \(m=\lvert E_k\rvert\),设 \(E_k=\{a_1(=k),a_2,\cdots,a_m\}\)。
那么根据等价类的定义,对于每一个 \(a_i\) 都存在一个 \(p_i\in G\) 满足 \(k\overset{p_i}{\rightarrow} a_i\)。
设置换集合 \(G_i=Z_k\circ p_i\),显然有 \(G_i\le G\),换而言之 \(G_i\) 中任何一个置换都可以让 \(k\) 变成 \(a_i\)。
容易发现 \(i\ne j\) 时 \(G_i\cap G_j=\varnothing\),这时因为 \(G_i\) 和 \(G_j\) 对 \(k\) 的作用时截然不同的。
所以满足 \(G_1+G_2+\cdots+G_m\subseteq G\),因为 \(G_1+G_2,\cdots,G_m=G_1\cup G_2\cup\cdots\cup G_m\)。
对于 \(\forall p\in G\),因为等价类的定义,都一定存在 \(k\xrightarrow{p}a_i\)。
所以就有 \(k\xrightarrow{p}a_i\xrightarrow{{p_i}^{-1}}k\),也就是 \(p\circ {p_i}^{-1}\in Z_k\),换而言之 \(p\in Z_k\circ {p_i}^{-1}\),也就是 \(p\in G_i\)。
那么就有 \(G\subseteq G_1+G_2+\cdots+G_m\),也就是证明了 \(G=G_1+G_2+\cdots+G_m\)。
因为 \(G_i=Z_k\circ p_i\),所以 \(\lvert G_i\lvert =\lvert Z_k\rvert\),也就是 \(\lvert G\rvert=\lvert Z_k\rvert\times\lvert E_k\rvert\)。
Burnside 引理
我们定义等价类的个数为 \(Ans\),其实在实际应用中 \(Ans\) 就是实际不同的答案,那么满足:
设 \(m=\lvert G\rvert\),\(G=\{a_1,a_2,\cdots,a_m\}\)。
设 \(s_{i,k}=[k\xrightarrow{a_i}k]\),那么能够发现 \(\sum\limits_{k=1}^n s_{i,k}=c(a_i)\) 而且 \(\sum\limits_{i=1}^m s_{i,k}=\lvert Z_k\rvert\)。
那么有 \(\sum\limits_{i=1}^m c(a_i)=\sum\limits_{i=1}^n \lvert Z_i\rvert=\sum\limits_{i=1}^n\sum\limits_{k=1}^m s_{i,k}\),\(\sum\limits_{i=1}^n \lvert Z_i\rvert=\sum\limits_{t=1}^{Ans}\sum\limits_{i\in E_t} \lvert Z_i\rvert\)。
因为同一个等价类的 \(Z\) 集合大小都是一样的,所以 \(\sum\limits_{i=1}^n\lvert Z_i\rvert=\sum\limits_{i=1}^{Ans} \lvert E_i\rvert\times \lvert Z_i\rvert\)。
然而有因为 \(\lvert Z_k\rvert\times\lvert E_k\rvert=\lvert G\rvert\),所以 \(\sum\limits_{i=1}^n =Ans\times \lvert G\rvert=\sum\limits_{p=1}^m c(a_i)\)。
那么就得到了 \(Ans=\dfrac{1}{\lvert G\rvert}\times \sum\limits_{p\in G} c(p)\)。
应用
\(2\times 2\) 方格中每个格子可以选择染上 \(2\) 种颜色(红色或白色)。
现在要问,如果不旋转、顺时针旋转 \(90\) 度、逆时针旋转 \(90\) 度、旋转 \(180\) 度后相同的均算成同一种方案,问总共有多少种不同的染色方案。
那么我们将所有染色方案都进行标号,得到:
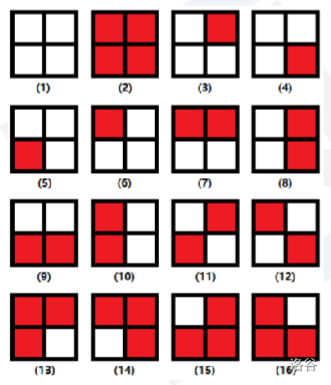
那么对于不旋转的 \(f_1\) 有:
那么右旋 \(90\) 度的 \(f_2\) 有:
后面的都是类似的。
那么对于 \(f_2\),没有改变的元素为 \(\{1,2\}\),所以 \(c(f_2)=2\)。
一次类推可以得到:\(c(f_1)=16\),\(c(f_3)=2\),\(c(f_4)=4\)。
所以我们得到:
Pólya 定理
注意到用上面的 Burnside 定理的元素是染色方案,其序列长度是指数级的。
而 Pólya 定理处理的元素是染色的位置,可以有效的降低复杂度。
设 \(G\) 是 \(n\) 个位置的置换群,有 \(m\) 中颜色,那么染色方法为:
其中 \(T(p)\) 指在置换 \(p\) 下不改变的染色方案的数量。
假设 \(G'\) 是把位置作为状态的置换群,那么可以发现把染色方案作为整体的置换和把位置作为元素的置换是有对应关系的,换而言之就是 \(\lvert G\rvert=\lvert G'\rvert\)。
那么通过 Burnside 引理可以得到:\(\dfrac{1}{\lvert G'\rvert}\times \sum\limits_{p'\in G'} c'(p')\),其中 \(c'(p')\) 表示 \(p'\) 在 \(G\) 中对应的置换 \(p\) 的不动点个数。
容易发现其实 \(c'(p')\) 和 \(T(p)\) 是等价的。
考虑怎么计算 \(T(p)\),设 \(D(p)\) 为置换 \(p\) 的阶数,那么根据乘法原理可以得到 \(T(p)=m^{D(p)}\)。
应用
同样的问题:
\(2\times 2\) 方格中每个格子可以选择染上 \(2\) 种颜色(红色或白色)。
现在要问,如果不旋转、顺时针旋转 \(90\) 度、逆时针旋转 \(90\) 度、旋转 \(180\) 度后相同的均算成同一种方案,问总共有多少种不同的染色方案。
那么现在我们对位置进行编号:
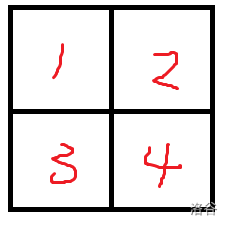
对于不动的置换 \(f_1'\) 有:
对于 Burnside 引理中的置换,\(f_1'\) 对应 \(f_1\):
所以根据原始的定义有 \(c'(f'_1)=c(f_1)=16\),另外 \(f'_1=(1)(2)(3)(4)\),所以 \(T(f_1')=2^4=16\)。
对于右旋 \(90\) 的置换 \(f'_2\) 有:
对于 Burnside 引理中的置换,\(f_2'\) 对应 \(f_2\):
所以根据原始的定义有 \(c'(f'_2)=c(f_2)=2\),另外 \(f'_2\) 本身就是一个循环置换,所以 \(T(f_2')=2^1=2\)。
