1. 摘要
在视觉三维重建中,要获取稠密的三维点云,通常采用面结构光来实现。但是作为普通的开发者,昂贵的工业相机、投影仪、工装等设备令人望而却步。如何利用手上常见的设备,实现稠密点云重建呢?
早在 1998 年,Jean-Yves Bouguety 与 Pietro Perona 就思考过类似这样的问题,他们发表了一篇名为 《3D photography on your desk》的论文,在论文中作者凭借极其简单的硬件(相机、点光源、铅笔/细棒、标定板,桌子)实现了稠密的3D重建,其重建误差可控制在0.1%以内。该方法甚至可以推广,利用太阳光实现汽车外形的三维重建,误差可在0.5%以内。
 |
 |
|---|---|
| a) 天使雕塑重建 | b) 汽车外形重建 |
2. 原理
 |
|---|
| 系统构成 |
作者设计的重建系统非常精妙,如上图所示:相机、点光源、细棒这三者构成测量装置,将被测物放置在桌面上,然后手持细棒并缓慢移动,令细棒投影缓慢扫过被测物。基于这些图像序列即可完成三维重建。
整个系统一共有三个物体需要提前固定,并完成相应的标定。即相机、桌面、点光源。其中相机内参和桌面平面方程可以在标定相机时一起得到(标定板放置在桌面上,通过标定时的位置外参可以得到)。而点光源则通过一个高度已知的铅笔,放置在桌面上,摆放多个位置后,由最小二乘计算得到。
因此,完整的实验步骤包括:
- 相机标定
- 光源标定
- 重建图像序列采集
2.1 相机标定
相机标定需要棋盘格标定板一个,相机固定后,在被测物物体所在区域将标定板摆放多个位姿,最后一个位姿中,标定板平放在桌面上。
标定算法可使用张氏标定(OpenCV自带),标定完成后,可以得到最后一个位姿下的标定板平面相对于相机光心的外参(RT),从而求得标定板平面的参数(如点法式,平面上一点,平面的法向量)。如果标定板很厚。假设厚度为 \(d\),可以将平面点沿着法向量平移 \(d\),从而得到桌面的平面参数 \(\Pi_d\)。
2.2 光源标定
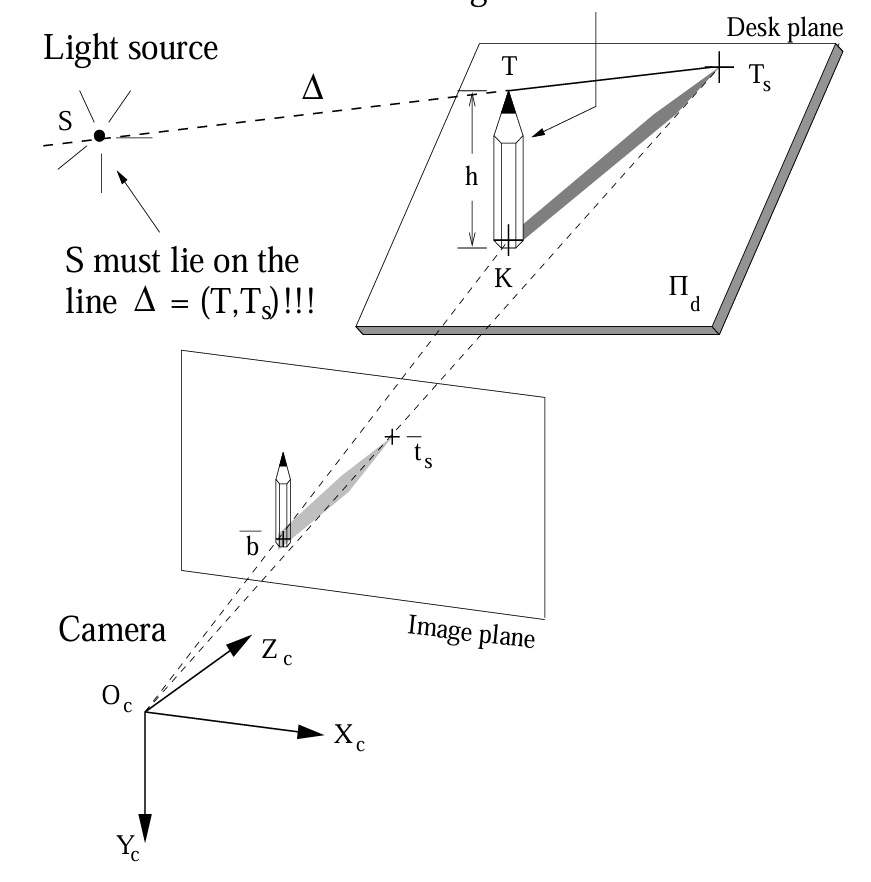 |
|---|
| 光源标定原理 |
如上图所示,将一个长度为 \(h\) 的铅笔垂直立在桌面 \(\Pi_d\) 上,铅笔笔尖为 \(T\) ,笔尾为 \(K\) ,光源 \(S\) 投射的光线经笔尖 \(T\) 与桌面 \(\Pi_d\) 相交于 \(T_s\) 点,相机采集到的铅笔图像中,笔尖像素点为 \(\bar{t}_s\) ,笔尾像素点为 \(\bar{b}\) 。根据成像原理,相机光心 \(O_c\) 与 笔尖像素点 \(\bar{t}_s\) 的连线与桌面 \(\Pi_d\) 相交于笔尖投影点 \(T_s\);同理相机光心 \(O_c\) 与 笔尾像素点 \(\bar{b}\) 的连线与桌面 \(\Pi_d\) 相交于笔尾投影点 \(K\) 。
而桌面 \(\Pi_d\) 在相机标定完成后已知,因此我们可以很容易求得笔尖投影点 \(T_s\) 和笔尾投影点 \(K\) ,另外铅笔高度 \(h\) 已知,因此结合桌面 \(\Pi_d\) 的法向量可以得到笔尖 \(T\) 的坐标。直线 \(TT_s\) 过光源 \(S\) 。
当移动铅笔时,上述关系始终成立,因此可以得到若干条经过光源 \(S\) 的直线,通过联立求最小二乘,即可计算出光源 \(S\) 的坐标(相机坐标系下)。
 |
|---|
| 光源标定示意图 |
2.3 重建序列采集
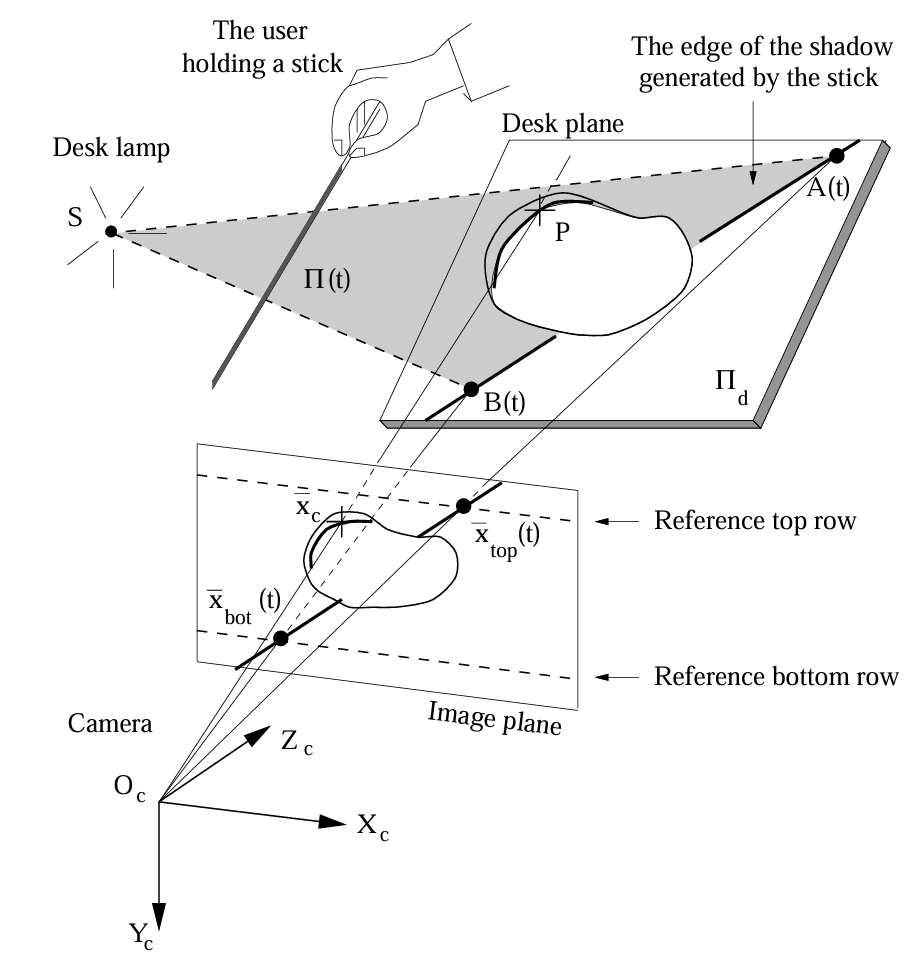 |
|---|
| 三维重建原理 |
如上图所示,手持一根细棒在被测物体上面移动,在某一时刻 \(t\) ,细棒经光源 \(S\) 照射产生一个投影平面 \(\Pi(t)\) ,投影平面在物体上被待测物体和桌面调制,设桌面细棒上部投影一点为 \(A(t)\) ,下部投影一点为 \(B(t)\) ,物体上细棒投影区域上某点为 \(P\)。则根据投影原理,以上三点均在投影平面 \(\Pi(t)\) 上 。而根据成像原理,上述三点与相机光心 \(O_c\) 的连线分别交相平面于 \(\bar{x}_{top}(t)\) 、\(\bar{x}_{bot}(t)\) 、\(\bar{x}_c\) 。
因此当拍摄到某一时刻下的图像后,假设物体居中,两侧仍留有桌面细棒投影。分别取上部和下部细棒投影像素 \(\bar{x}_{top}(t)\) 和\(\bar{x}_{bot}(t)\),则光心 \(O_c\) 与 \(\bar{x}_{top}(t)\) 连线与桌面 \(\Pi_d\) 相交于 \(A(t)\) ,同理光心 \(O_c\) 与 \(\bar{x}_{bot}(t)\) 连线与桌面 \(\Pi_d\) 相交于 \(B(t)\) , 桌面 \(\Pi_d\) 已知,故可解算出 \(A(t)\) 和 \(B(t)\) 。而光源 \(S\) 已知,因此细棒投影面 \(\Pi(t)\) 可根据这三点表示出来。而物体表面某一代求的三维点 \(P\) 可通过其像素点 \(\bar{x}_c\) 与 \(O_c\) 的连线与细棒投影面 \(\Pi(t)\) 相交求得。
 |
|---|
| 重建原理示意图 |
在细棒投影面上,物体表面所有与投影面相交的点都可通过上述方法计算得到,而细棒投影在某时刻下的投影沿投影面是连续的。而当细棒缓慢移动,扫过待测物体表面时,若图像采集速度大于移动速度时,则可得到连续的投影,如此一来,整个待测物体表面均可得到重建的点,最终可得到稠密点云。
2.4 投影计算处理
所采集到的连续多张投影序列图像实际上构成了空间和时间。细棒从一端缓慢移动到另一端,而细棒是有宽度的,所以得到的投影并非一条线,而是有宽度的投影区域。所以假设细棒阴影在图像中从左侧移动到右侧,则我们在处理参与重建计算的投影点时,只处理阴影的右边缘点(即前进方向所指的边缘点)。
这里主要需处理每个时刻 \(t\) 下的细棒边缘点 \(\bar{x}_{top}(t)\) 、\(\bar{x}_{bot}(t)\) 的定位以及该时刻下,细棒边缘所经过的每个可重建像素点 \(t_s(\bar{x}_c)\) 。
2.4.1 差分图像提取
所采集到的图像其中既包含物体自身所形成的阴影还包含细棒阴影,并且阴影的边界通常不是陡变的,因此不方便提取精确的边缘点。这里利用图像序列做如下处理:
整个序列中,每个像素的最大亮度和最小亮度值(灰度值)可表示为:
则每个像素的阈值为:
细棒阴影边缘位置可以定义为图像 \(I(x,y,t)\) 与阈值图像 \(I_{shadow}(x,y)\) 在时空域中相交的位置,可看作是差分图像:
的过零点位置。
2.4.2 细棒边缘点与重建像素点定位
对于每一帧图像,在拍摄时都应该使得细棒阴影超出被测物体的上下区域,得到直接投影在桌面上的直线阴影,这样方便定位出细棒右侧投影平面上的点 \(\bar{x}_{top}(t)\) 、\(\bar{x}_{bot}(t)\) 。
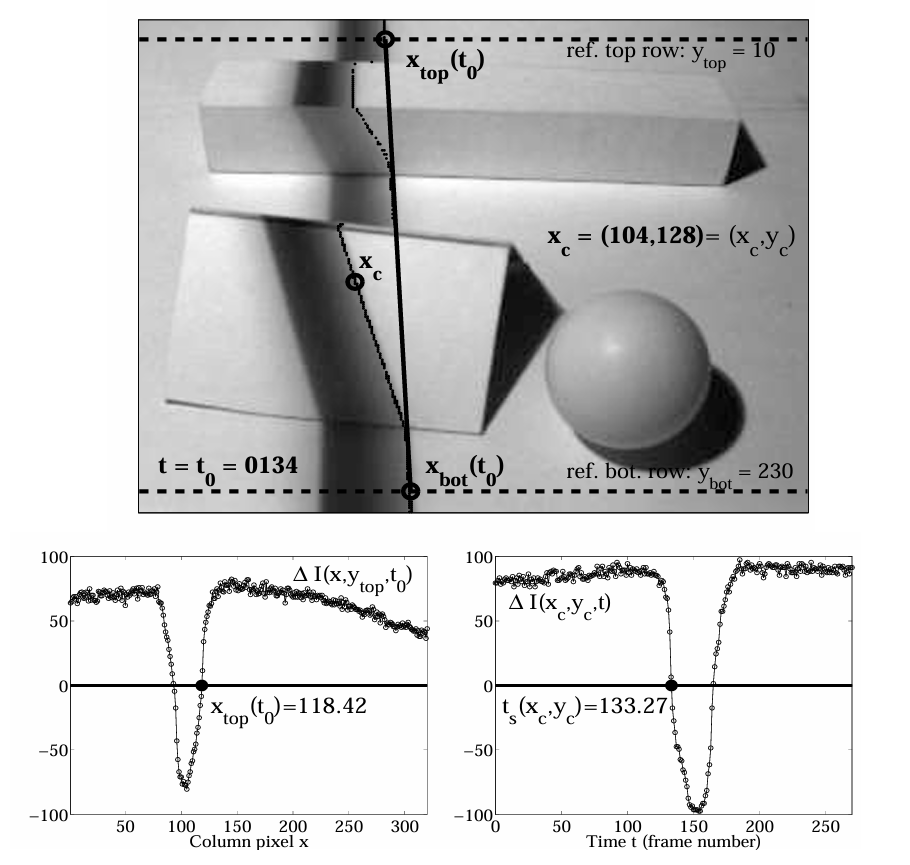 |
|---|
| 细棒边缘点与重建像素点提取 |
如上图所示, \(t_0\) 时刻下,计算得到差分图像 \(\Delta I(x,y,t_0)\) ,那么顶部 \(y_{top} = 10\) (可根据实际情况取固定值)处整行差分灰度值的分布情况如左下图曲线所示,那么 \(x_{top}(t_0)\) 即为该曲线的二次过零点。同理可得 \(x_{bot}(t_0)\) 。而对于待重建像素点 \(\bar{x}_c\) ,将所有差分图像,在 \((x_c,y_c)\) 所在区域的差分灰度值绘制为曲线,那么曲线的一次过零点即为 \(\bar{x}_c\) 。
2.4.3 非重建像素点滤除
在某帧图像中,只有细棒投影边缘上的点才参与重建,因此为了滤除其他不参与重建的点(如物体自身投影),可计算每个像素的对比度:
只有对比度大于阈值 \(I_{thresh}\) 时,才处理,否则跳过。
2.4.4 实时处理加速算法
尽管计算\(I_{shadow}\)需要用到\(I_{min}\)和\(I_{max}\),但该算法存在一种无需在内存中存储完整图像序列的实现方式,这使得实时处理成为可能。具体实现方式如下:在采集图像\(I(x,y,t)\)的过程中,逐帧更新五个数组,分别是\(I_{max}(x,y)\)、\(I_{min}(x,y)\)、\(I_{contrast}(x,y)\)、\(I_{shadow}(x,y)\)以及阴影时间\(t_s(x,y)\)。对于某个特定像素\((x,y)\),在图像序列开始时(第一帧)记录其最大亮度值\(I_{max}(x,y)\);随后,随着时间推移,利用后续输入的图像更新该像素的最小亮度值\(I_{min}(x,y)\)和对比度\(I_{contrast}(x,y)\)。当对比度\(I_{contrast}(x,y)\)超过阈值\(I_{thresh}\)时,开始计算并逐帧更新自适应阈值\(I_{shadow}(x,y)\)(此时阈值被激活)。这一过程会持续进行,直到该像素的亮度值$$I(x,y,t)$$首次(沿上升方向)超过阈值\(I_{shadow}(x,y)\),此时记录的时间即为该像素的阴影时间\(t_s(x,y)\)。在这种实现方式中,跟踪的是阴影的左边缘而非右边缘,但方法原理保持不变。
2.4.5 非理想点光源可能存在的问题
实验发现,这种基于阈值的阴影边缘检测方法能够在一定程度上应对场景中的内部反射问题。然而,若光源并非理想的点光源,那么取最大亮度与最小亮度的平均值作为阈值图像 \(I_{shadow}\) 的阈值,可能并非始终是最优选择。实际上,随着细杆与物体表面距离的增加,阴影边缘的轮廓会逐渐变得平缓;同时,随着物体表面法向量的变化,阴影边缘轮廓还会发生不对称变形。这些因素都会给阴影边界点的检测带来困难。未来,研究团队计划建立扩展光源的几何模型,并将其融入到该系统中。
3. 实现
 |
 |
|---|---|
| a) 重建序列图像 | b) 重建结果 |
项目地址:GShang2018/3D-photography-on-your-desk
4. 参考资料
- sci.utah.edu/~gerig/CS6320-S2015/Materials/CS6320-CV-S2015-StructuredLight.pdf

 在视觉三维重建中,要获取稠密的三维点云,通常采用面结构光来实现。但是作为普通的开发者,昂贵的工业相机、投影仪、工装等设备令人望而却步。如何利用手上常见的设备,实现稠密点云重建呢?早在 1998 年,Jean-Yves Bouguety 与 Pietro Perona 就思考过类似这样的问题,他们发表了一篇名为 《3D photography on your desk》的论文,在论文中作者凭借极其简单的硬件(相机、点光源、铅笔/细棒、标定板,桌子)实现了稠密的3D重建,其重建误差可控制在0.1%以内。该方法甚至可以推广,利用太阳光实现汽车外形的三维重建,误差可在0.5%以内。
在视觉三维重建中,要获取稠密的三维点云,通常采用面结构光来实现。但是作为普通的开发者,昂贵的工业相机、投影仪、工装等设备令人望而却步。如何利用手上常见的设备,实现稠密点云重建呢?早在 1998 年,Jean-Yves Bouguety 与 Pietro Perona 就思考过类似这样的问题,他们发表了一篇名为 《3D photography on your desk》的论文,在论文中作者凭借极其简单的硬件(相机、点光源、铅笔/细棒、标定板,桌子)实现了稠密的3D重建,其重建误差可控制在0.1%以内。该方法甚至可以推广,利用太阳光实现汽车外形的三维重建,误差可在0.5%以内。