1. 离散动作空间的策略网络
在离散空间中,动作是可数的,例如:{左, 右, 上, 下} 或 {加速, 刹车}。
网络架构与处理方式
-
输出层:Softmax
-
策略网络的最后一层是一个 Softmax 层。
-
假设有
N个可选动作,网络会输出一个长度为N的向量。 -
Softmax 函数确保这个向量的所有元素都在 (0, 1) 之间,且和为 1。这样,每个元素就代表了选择对应动作的概率。
-
-
策略表示
-
策略
π(a|s)直接由网络输出给出:π(a=i|s) = Softmax(Logits(s))[i]
-
-
动作采样
-
根据网络输出的概率分布,进行分类采样来选择动作。
-
在 Python 中,可以使用
np.random.choice或torch.distributions.Categorical。
-
import torch import torch.nn as nn import torch.nn.functional as Fclass DiscretePolicyNetwork(nn.Module):def __init__(self, input_dim, hidden_dim, output_dim):super(DiscretePolicyNetwork, self).__init__()self.fc1 = nn.Linear(input_dim, hidden_dim)self.fc2 = nn.Linear(hidden_dim, output_dim) # output_dim = 动作数量def forward(self, state):x = F.relu(self.fc1(state))logits = self.fc2(x) # 输出 logits,未归一化的概率return logitsdef act(self, state):logits = self.forward(state)# 创建分类分布action_probs = F.softmax(logits, dim=-1)dist = torch.distributions.Categorical(action_probs)# 采样动作action = dist.sample()# 计算对数概率,用于策略梯度更新log_prob = dist.log_prob(action)return action.detach().item(), log_prob# 假设有4个动作 policy_net = DiscretePolicyNetwork(input_dim=8, hidden_dim=128, output_dim=4) state = torch.tensor([0.1, 0.5, -0.2, ...]) # 状态向量 action, log_prob = policy_net.act(state) print(f"Sampled action: {action}")
2. 连续动作空间的策略网络
在连续空间中,动作是实数向量,例如:方向盘转角 [-1, 1],机器人关节扭矩 [τ₁, τ₂, ...]。
这里有两种主要设计思路:
A. 随机策略 - 输出分布参数
这是最常用的方法,策略网络输出一个概率分布的参数,动作从这个分布中采样。
-
输出层:分布参数
-
最常用的是高斯分布。网络为每个动作维度输出两个值:
-
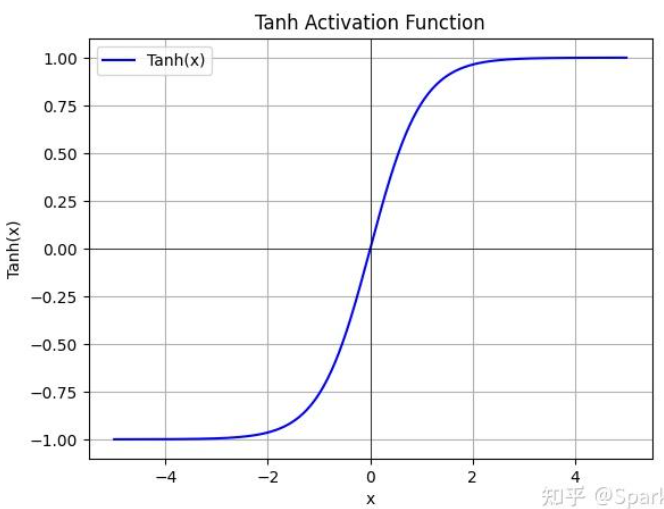
均值:通常使用
tanh作为激活函数,将均值限制在[-1, 1]范围内,或者不适用激活函数。 -
标准差:通常使用
softplus等函数确保其为正数。也可以是一个与状态无关的可学习参数。
-
-
-
策略表示
-
策略
π(a|s)是一个概率密度函数。例如,对于高斯分布:a ~ N(μ(s), σ(s)²)
-
-
动作采样
-
使用网络输出的均值和标准差构建一个高斯分布,然后从这个分布中采样。
-
由于采样操作不可导,在训练时需要使用重参数化技巧。
-
class ContinuousPolicyNetwork(nn.Module):def __init__(self, input_dim, hidden_dim, output_dim):super(ContinuousPolicyNetwork, self).__init__()self.output_dim = output_dim # 动作空间的维度self.fc1 = nn.Linear(input_dim, hidden_dim)# 输出均值self.mean_head = nn.Linear(hidden_dim, output_dim)# 输出对数标准差(更稳定),通常作为一个独立的层self.log_std_head = nn.Linear(hidden_dim, output_dim)# 或者:self.log_std = nn.Parameter(torch.zeros(1, output_dim))def forward(self, state):x = F.relu(self.fc1(state))mean = torch.tanh(self.mean_head(x)) # 将均值限制在[-1,1]log_std = self.log_std_head(x)# 使用 clamp 将标准差限制在一个合理范围内log_std = torch.clamp(log_std, min=-20, max=2)std = torch.exp(log_std)return mean, stddef act(self, state):mean, std = self.forward(state)# 创建多元高斯分布(假设各维度独立)dist = torch.distributions.Normal(mean, std)# 重参数化技巧采样action = dist.rsample()# 计算对数概率(对于多维动作,需要对数概率的和)log_prob = dist.log_prob(action).sum(dim=-1)# 如果需要将动作限制在[-1,1],可以使用tanh,但需要修正对数概率# action = torch.tanh(raw_action)# 更复杂的实现会处理tanh变换后的概率计算return action.detach().numpy(), log_prob# 假设动作是2维的(如:速度,方向) policy_net = ContinuousPolicyNetwork(input_dim=8, hidden_dim=128, output_dim=2) state = torch.tensor([0.1, 0.5, -0.2, ...]) action, log_prob = policy_net.act(state) print(f"Sampled continuous action: {action}")
torch.clamp 将输入张量中的所有元素限制在一个指定的区间 [min, max] 内。具体来说:
-
如果元素小于
min,则将其设置为min -
如果元素大于
max,则将其设置为max -
如果元素在
[min, max]范围内,则保持不变
tanh函数:
torch.distributions.Normal 表示一个一元高斯分布,由两个参数定义:
-
loc: 分布的均值 -
scale: 分布的标准差
# 创建分布 mean = torch.tensor([0.0, 1.0]) std = torch.tensor([1.0, 0.5]) normal = dist.Normal(mean, std)# 1. sample() - 普通采样 samples = normal.sample() print("Sample:", samples) # 输出: tensor([-0.1234, 1.2345])# 2. rsample() - 重参数化采样(可微分) reparam_samples = normal.rsample() print("Reparameterized sample:", reparam_samples) # 输出: tensor([0.5678, 0.8765])# 3. sample() 批量采样 batch_samples = normal.sample((3,)) # 采样3次 print("Batch samples shape:", batch_samples.shape) # 输出: torch.Size([3, 2])
