由于网上没有找到直接的代码,就来写一下。
原理部分可以回去看高数,核心就是以直线的斜率和截距为变量,让误差最小化。以下是代码部分
import numpy as np
import matplotlib.pyplot as pltdef linear_least_squares(q_list, n_list):"""最小二乘法直线拟合参数:q_list: x坐标数据列表n_list: y坐标数据列表返回:slope: 直线斜率intercept: 直线截距fig: 图像对象"""# 将列表转换为numpy数组x = np.array(q_list)y = np.array(n_list)# 计算必要的数据和n = len(x)sum_x = np.sum(x)sum_y = np.sum(y)sum_xy = np.sum(x * y)sum_x2 = np.sum(x ** 2)# 计算斜率和截距slope = (n * sum_xy - sum_x * sum_y) / (n * sum_x2 - sum_x ** 2)intercept = (sum_y - slope * sum_x) / n# 计算拟合的y值y_fit = slope * x + intercept# 计算相关系数R²y_mean = np.mean(y)ss_tot = np.sum((y - y_mean) ** 2)ss_res = np.sum((y - y_fit) ** 2)r_squared = 1 - (ss_res / ss_tot)# 创建图像fig, ax = plt.subplots(figsize=(10, 6))# 绘制原始数据点ax.scatter(x, y, color='blue', label='original data', s=50, alpha=0.7)# 绘制拟合直线ax.plot(x, y_fit, color='red', linewidth=2, label=f'Fitted Line: y = {slope:.4f}x + {intercept:.4f}')# 设置图表属性ax.set_xlabel('q', fontsize=12)ax.set_ylabel('n', fontsize=12)ax.set_title('Least Squares Linear Fit', fontsize=14)ax.legend(fontsize=10)ax.grid(True, alpha=0.3)# 在图上显示参数textstr = f'Slope: {slope:.4f}\nIntercept: {intercept:.4f}\nR²: {r_squared:.4f}'ax.text(0.05, 0.95, textstr, transform=ax.transAxes, fontsize=10,verticalalignment='top', bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))plt.tight_layout()return slope, intercept, fig# 实例
q_list = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
n_list = [2.1, 4.2, 5.8, 8.1, 9.9, 12.1, 13.8, 16.2, 17.9, 20.1]# 调用拟合函数
slope, intercept, fig = linear_least_squares(q_list, n_list)# 打印结果
print(f"直线方程: y = {slope:.4f}x + {intercept:.4f}")
print(f"斜率: {slope:.4f}")
print(f"截距: {intercept:.4f}")# 显示图像
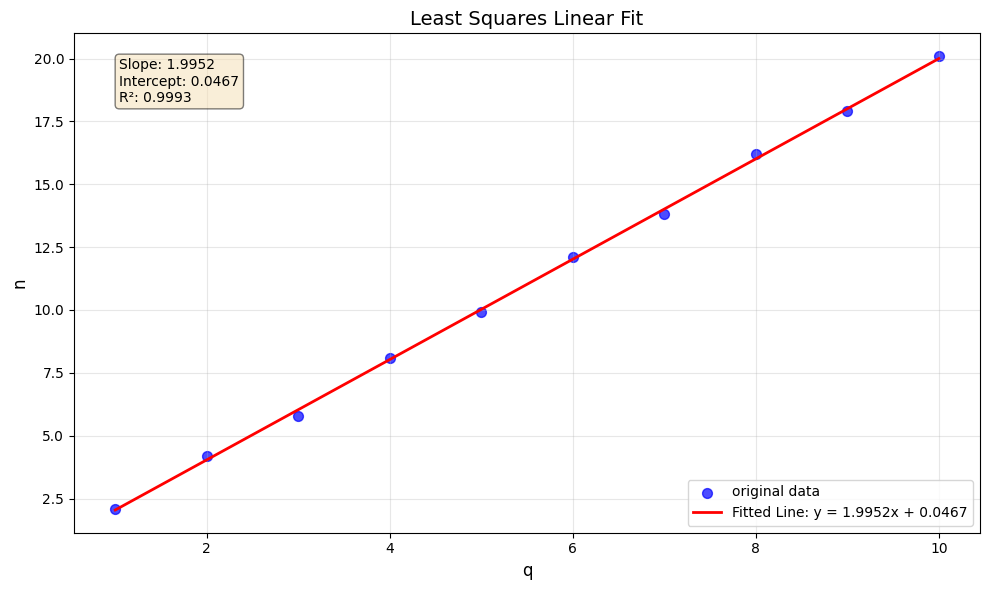
plt.show()运行结果:
直线方程: y = 1.9952x + 0.0467
斜率: 1.9952
截距: 0.0467