2.3 深度 Q 网络（Deep Q-Network, DQN）

深度 Q 网络（Deep Q-Network, DQN）

---

深度神经网络在函数逼近中的局限性

值函数型深度强化学习的目标是使用深度神经网络（DNN）逼近每个状态–动作对的 Q 值。
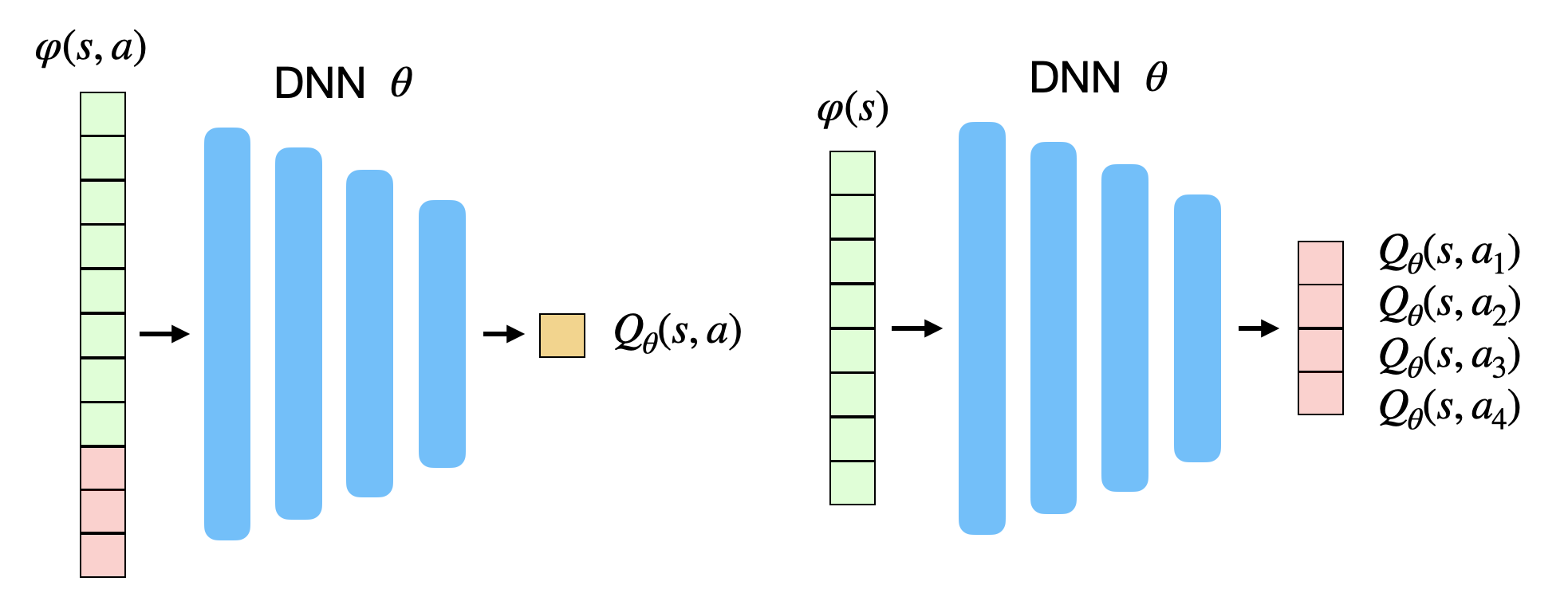
网络可以有两种形式（见下图）：

• 以状态–动作对 \((s,a)\) 为输入，输出对应的单个 Q 值；
• 以状态 \(s\) 为输入，输出所有可能动作的 Q 值（仅适用于离散动作空间）。

在 Q-learning 中，我们要最小化以下均方误差（MSE）损失函数：

\[\mathcal{L}(\theta) = \mathbb{E}_{(s,a,r,s')}[(r(s,a,s') + \gamma \max_{a'} Q_\theta(s',a') - Q_\theta(s,a))^2] \]

目标是减少预测误差，即 \(Q_\theta(s,a)\) 与真实回报（此处以 \(r(s,a,s') + \gamma \max_{a'} Q_\theta(s',a')\) 近似）之间的差距。

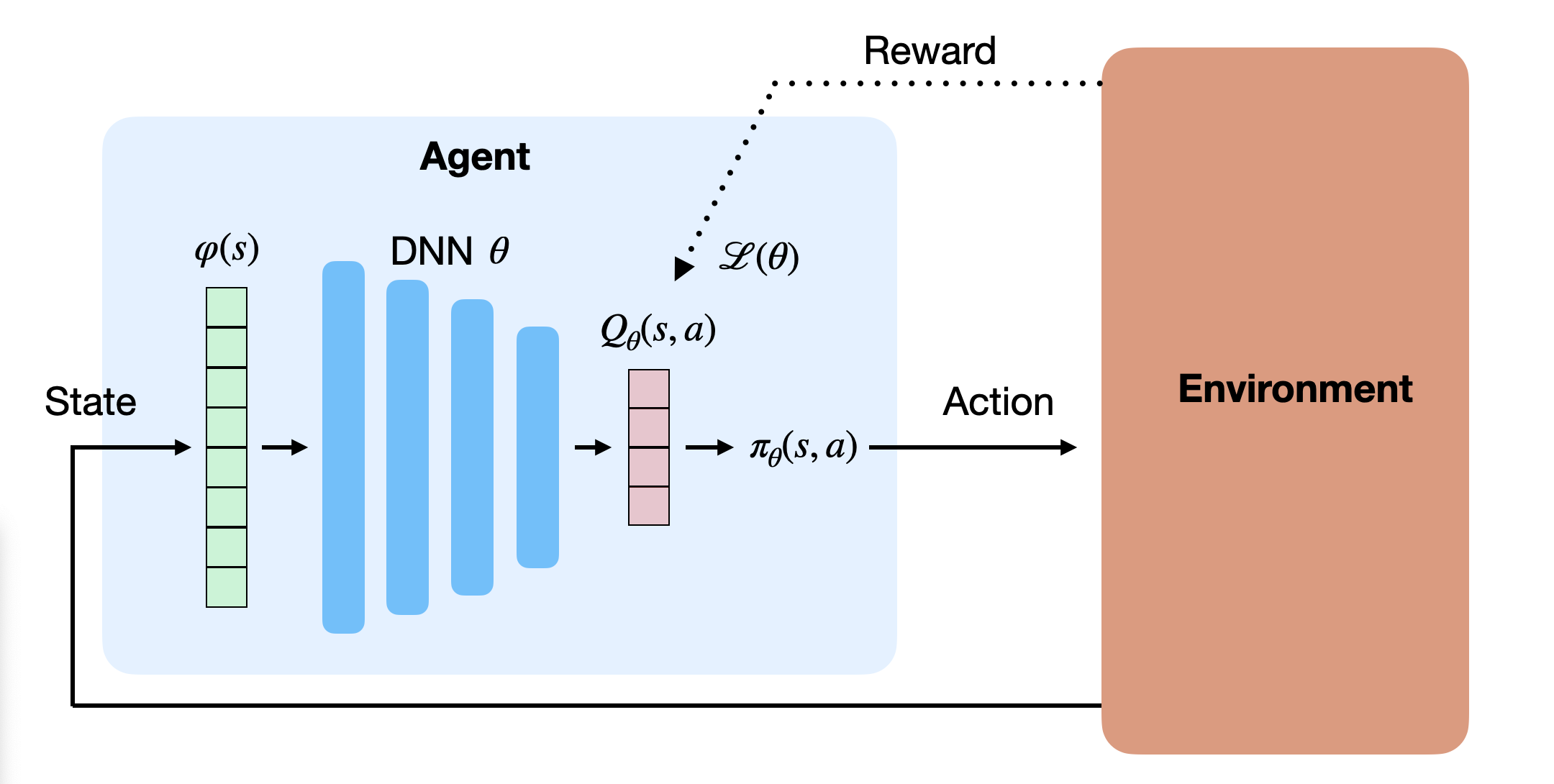
在实践中，我们收集若干样本 \((s,a,r,s')\)（即单步转移），打乱组成小批量（minibatch），并通过反向传播和 SGD 更新神经网络，从而间接改进策略。

---

相关输入问题（Correlated Inputs）

在与环境的在线交互中，连续采样的转移是高度相关的：
\((s_t,a_t,r_{t+1},s_{t+1})\) 紧跟 \((s_{t+1},a_{t+1},r_{t+2},s_{t+2})\)。
在电子游戏中，相邻帧几乎相同（仅少数像素变化），最优动作也往往连续相同。

深度网络对相关输入非常敏感：
若批量样本缺乏独立性（非 i.i.d.），SGD 将难以优化，模型易陷入局部最小值。
因此我们需要“打乱”样本，确保训练批次中的样本尽可能独立。

---

非平稳目标问题（Non-stationary Targets）

在传统的监督学习中，目标值 \(\mathbf{t}\) 是固定的；但在 Q-learning 中，目标值：

\[t = r(s,a,s') + \gamma \max_{a'} Q_\theta(s',a') \]

会随着训练不断变化，因为 \(Q_\theta(s',a')\) 自身在更新。
这导致训练目标是非平稳（non-stationary）的，模型容易出现不稳定或震荡收敛。

---

深度 Q 网络（DQN）

@Mnih2015（最早发表于 @Mnih2013）提出了两个关键改进，成功解决了上述问题，奠定了深度强化学习的基础。

---

经验回放机制（Experience Replay Memory）

为解决输入相关性问题，DQN 使用一个大型缓存区——经验回放池（Replay Buffer, ERM）。
智能体与环境交互产生的转移 \((s,a,r,s')\) 被存储到 ERM 中，
每次训练时从中随机采样小批量样本用于更新。

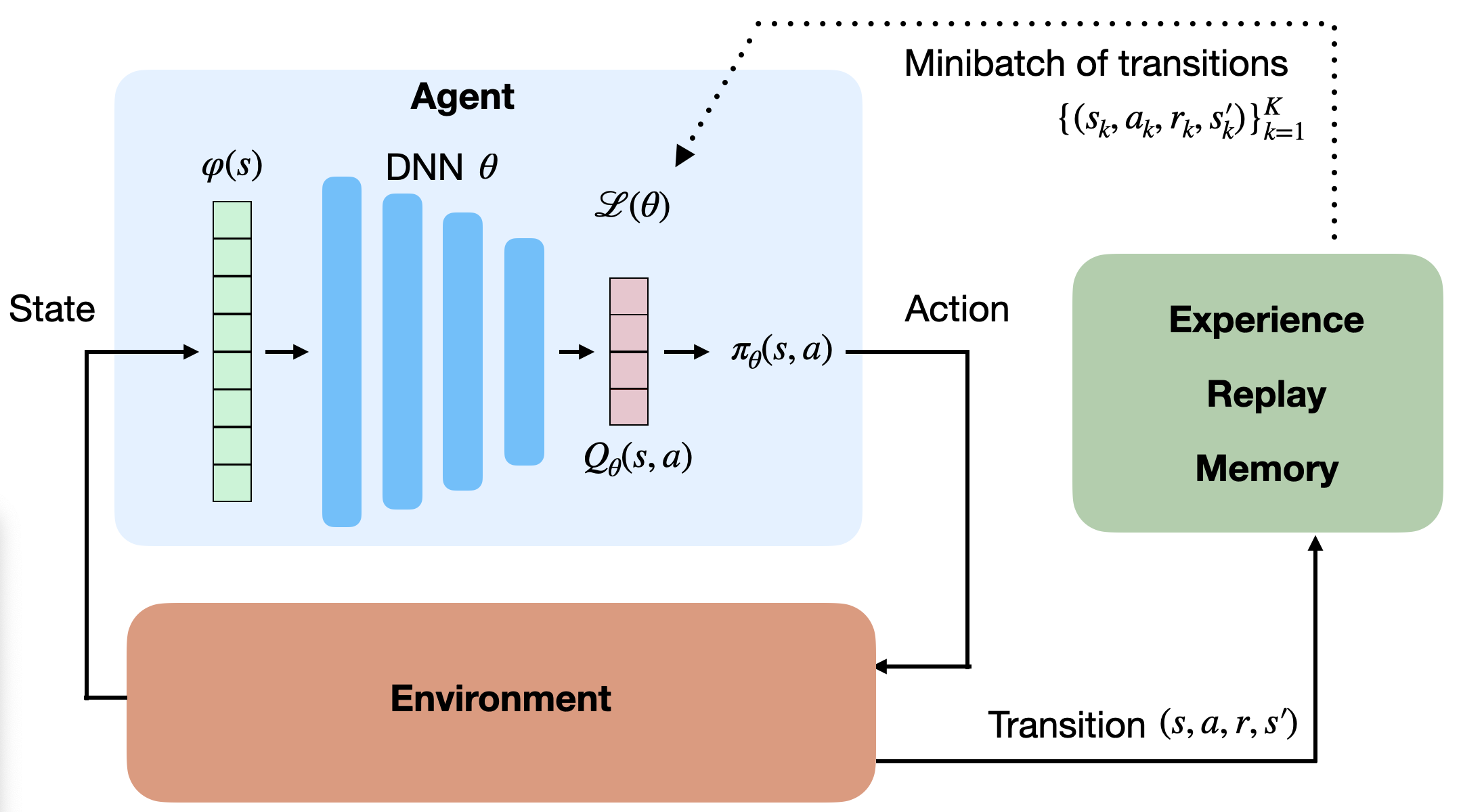
损失函数定义为：

\[\mathcal{L}(\theta) = \frac{1}{K} \sum_{k=1}^K (r_k + \gamma \max_{a'} Q_\theta(s'_k, a') - Q_\theta(s_k, a_k))^2 \]

这些样本虽然独立，但并非同分布，因为它们来自不同策略。
然而 Q-learning 是异策略（off-policy）方法，因此不受此影响。

只有异策略算法才能与经验回放机制结合使用。

---

目标网络（Target Network）

为解决目标非平稳问题，DQN 引入了第二个神经网络——目标网络（Target Network）。
目标网络参数 \(\theta'\) 与主网络参数 \(\theta\) 相同，但更新频率较低。

损失函数改写为：

\[\mathcal{L}(\theta) = \frac{1}{K} \sum_{k=1}^K (r_k + \gamma \max_{a'} Q_{\theta'}(s'_k,a') - Q_\theta(s_k,a_k))^2 \]

目标网络定期（如每 10000 步）从主网络复制参数：

\[\theta' \leftarrow \theta \]

这样目标值在较长时间内保持稳定，训练更加平稳。

---

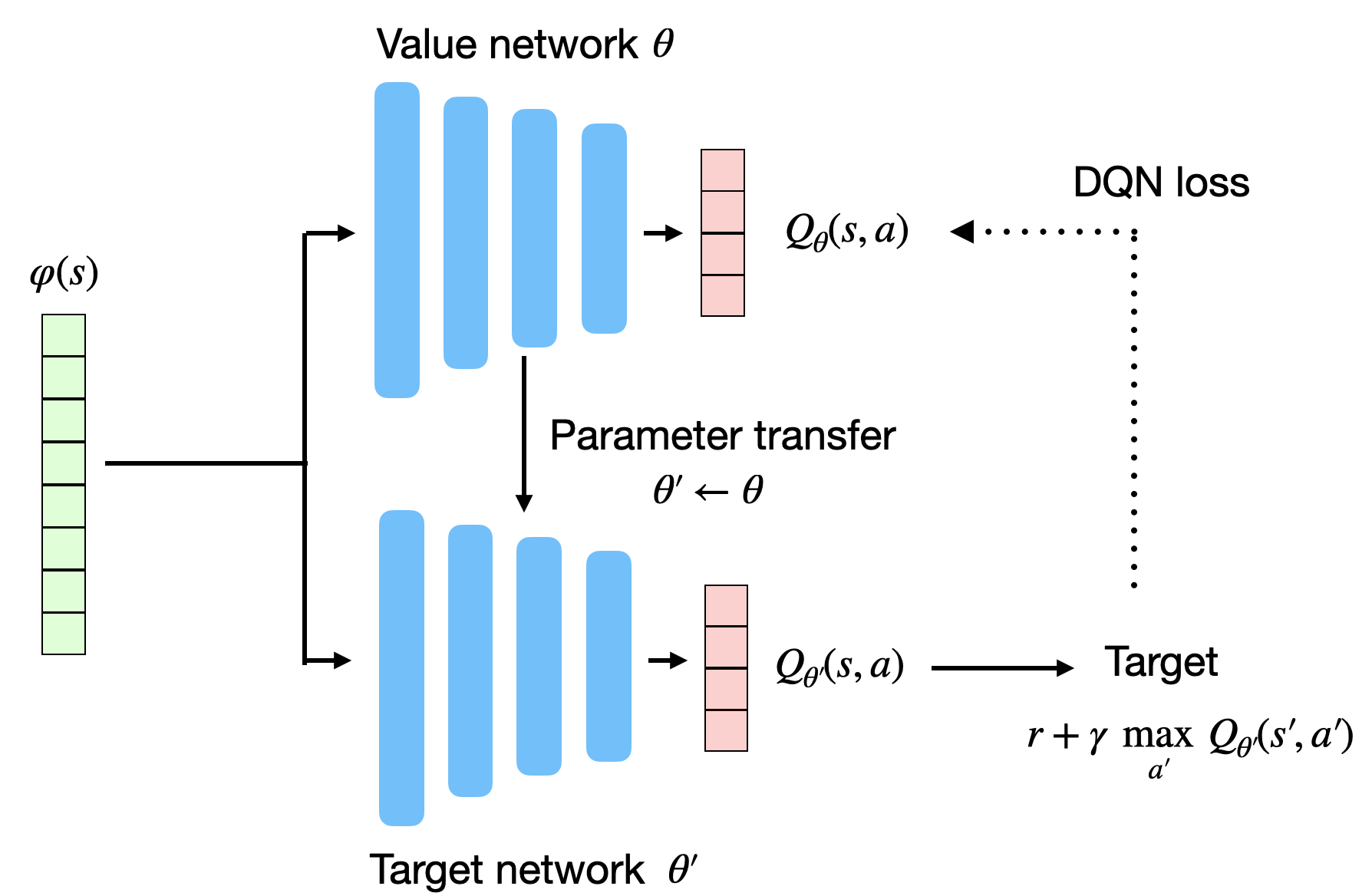
DQN 算法流程

DQN 核心算法：

1. 初始化主网络 \(Q_\theta\)；
2. 复制参数得到目标网络 \(Q_{\theta'}\)；
3. 初始化经验回放池 \(\mathcal{D}\)；
4. 观察初始状态 \(s_0\)；
5. 对每个时间步 \(t=1...T\)：
   • 按策略（如 \(\epsilon\)-greedy）选择动作 \(a_t\)；
   • 执行动作，得到 \(r_{t+1}, s_{t+1}\)；
   • 将转移 \((s_t,a_t,r_{t+1},s_{t+1})\) 存入 \(\mathcal{D}\)；
   • 每隔 \(T_\text{train}\) 步：
     • 从 \(\mathcal{D}\) 随机采样小批量；
     • 计算目标值 \(t = r + \gamma \max_{a'} Q_{\theta'}(s',a')\)；
     • 最小化损失 \(\mathcal{L}(\theta) = \mathbb{E}[(t - Q_\theta(s,a))^2]\)；
   • 每隔 \(T_\text{target}\) 步：
     • 更新目标网络：\(\theta' \leftarrow \theta\)。

在实践中，更新目标网络的方式也可采用软更新（soft update）：

\[\theta' = \tau \theta + (1 - \tau) \theta' \]

其中 \(\tau \in [0,1]\) 较小，使目标网络缓慢追踪主网络的参数。

---

DQN 的特点与局限

DQN 的两个特性使其学习速度较慢：

1. 经验回放导致样本被延迟使用；
2. 目标网络更新缓慢。

因此 DQN 的样本复杂度（sample complexity）很高——往往需要数百万次交互才能收敛。

---

DQN 在 Atari 游戏中的应用

DQN 最初被用于解决 Atari 2600 游戏问题。
输入为视频帧，动作空间为有限离散集合（上/下/左/右/射击等）。

网络结构包括：

• 两个卷积层（无池化层）；
• 两个全连接层；
• 输出层对应各个动作的 Q 值。

为克服部分可观测性问题（单帧不满足马尔可夫性），DQN 将最近4帧图像拼接为输入，使网络能学习出速度信息。
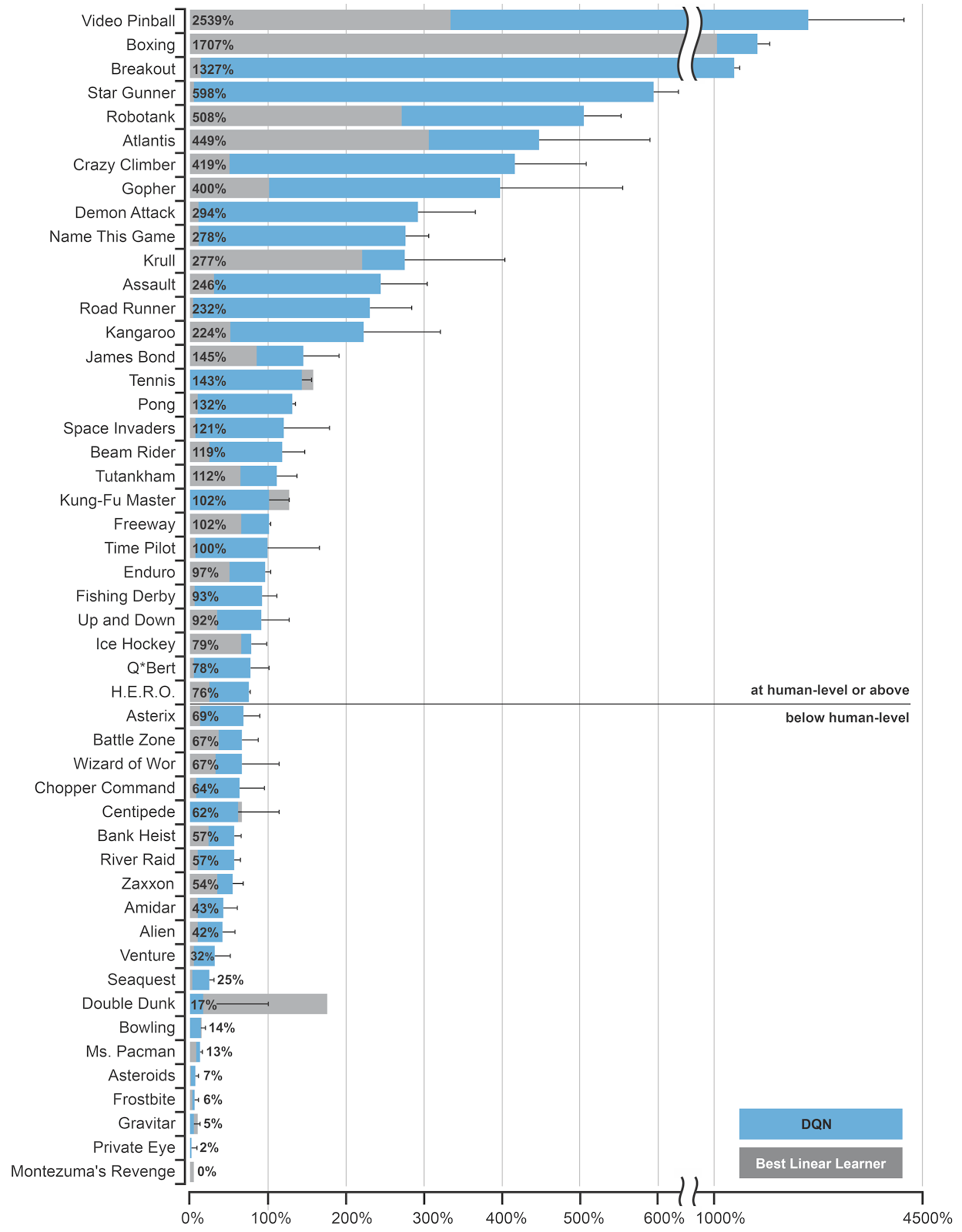
DQN 在部分游戏（如 Breakout、Pinball）上达到超人水平，但在需要长远规划的任务（如 Montezuma’s Revenge）上表现仍差。

---

为什么不使用池化层？

在图像分类中，池化层用于实现空间不变性（无论物体在图像何处都可识别）。
但在强化学习中，空间信息非常重要。
例如球的位置对决策至关重要，因此 DQN 不使用池化层，以保留精确位置信息。
缺点是参数量更大，对显存和样本需求更高。

---

总结

DQN 能在高维状态空间中，通过稀疏和延迟的奖励信号学习到有效策略。
它在 49 款 Atari 游戏上使用同一套网络结构与超参数实现了稳定表现，展示了深度强化学习的通用性与潜力。