题目
题目描述
多年前,Johnny 的父亲拥有一个伟大的王国。临终前,他将他的王国分给了他的儿子们(Johnny 和 Johnny 的兄弟)。Johnny 的兄弟得到了一个半径为 \(R\) 的圆形王国,Johnny 则得到了一个边长为 \(L\) 的正方形王国。由于 Johnny 在他的父亲去世非常后嫉妒他的兄弟,他决定将自己的王国扩展为一个圆形,使得正方形的四个角恰好位于圆的弧上。但问题在于 Johnny 可能会侵占他兄弟的一些土地,这可能引发兄弟之间的大战。因此 Johnny 决定说服他的兄弟修建一堵墙来分隔两个王国。这堵墙应连接两个圆的交点。你需要计算这堵墙的长度。
输入格式
第一行输入包含一个整数 \(T\),表示测试用例的数量。随后是 \(T\) 个测试用例,每个测试用例的第一行包含 \(6\) 个浮点数;前两个数字表示 Johnny 兄弟王国的圆心坐标,接下来两个数字表示 Johnny 王国的圆心坐标,\(R\) 表示 Johnny 兄弟王国的半径,\(L\) 表示 Johnny 王国正方形的边长。保证两个王国最初没有任何土地重叠。同时,在扩展王国 B 后,保证交叉区域不会完全覆盖 Johnny 兄弟的王国。所有十进制数的绝对值均小于 \(10^9\)。
输出格式
应输出 \(T\) 行,每行格式如下:
k. S
其中 \(k\) 是测试点编号(从 \(1\) 开始),一个点号,一个空格,\(S\) 是一个保留 \(3\) 位小数的十进制数,表示墙的长度。如果不可能发生战争,则输出 No problem。
输入输出样例 #1
输入 #1
3
0.0 0.0 10.0 0 3 3
0.0 0.0 4.121 0 3 3
-1 3 1 -1 2 7.071
输出 #1
1. No problem
2. 2.971
3. 3.994
说明/提示
本翻译由 deepseek 辅助生成
题解
前置知识
这道题可能涉及到以下内容。
- 三角函数
- 余弦定理
题目分析
这道题的解题思路与数学几何题类似,我们只需要推导出关系式就很好解决了。
下面是一张参考图:
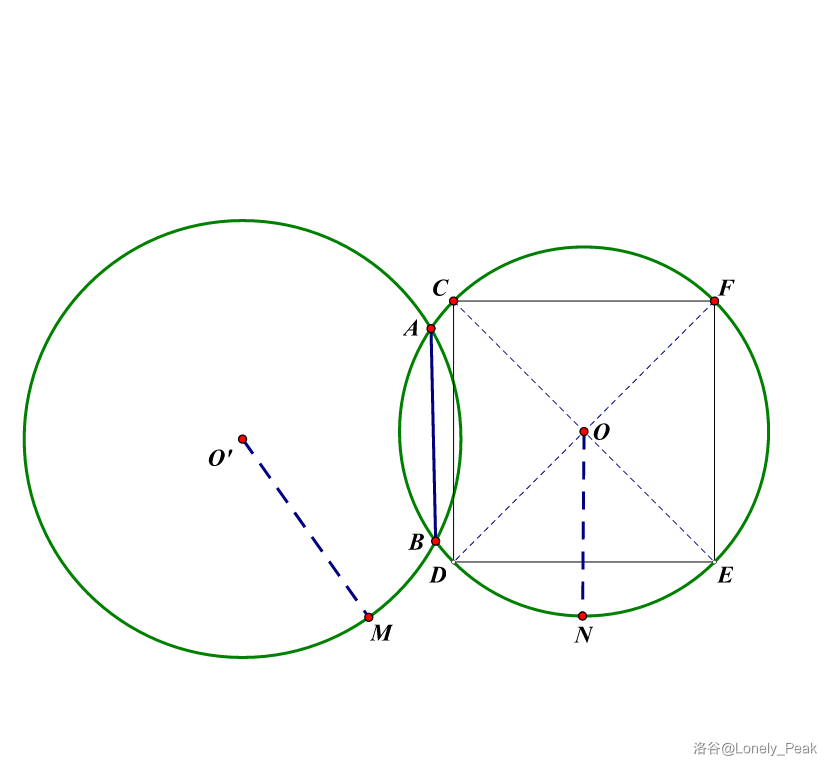
在图中,正方形 \(CFDE\) 的边长为 \(CF=EF=DE=DC\),Johnny 新扩展的圆半径为 \(NO\),需要修建的墙壁对应线段 \(AB\),而 Johnny 兄弟的圆半径为 \(O'M\)。
计算步骤:
已知正方形边长,根据等腰直角三角形的性质,外接圆半径等于对角线长度的一半:
根据两点间距离公式可以得出两圆心距离:
接下来就可以判断两圆是否相交了。
- 如果两圆心距离大于两圆半径之和(\(d > r + R\)),则两圆相离。
- 如果两圆心距离小于两圆半径之差的绝对值(\(d < |R - r|\)),则两圆内含。
如果出现以上两种情况,代表两圆不相交,输出 No problem。
如果两圆相交,公共弦长度计算公式为:
其中弦心距 \(a\) 可通过余弦定理求得:
代入后得到最终表达式:
将上述数学推导转化为程序实现就可以完成这道题了。
参考程序
#include <bits/stdc++.h>
#define int long long
#define Rint register int
#define fast_running ios::sync_with_stdio(false), cin.tie(nullptr)
using namespace std;signed main() {fast_running;int T, cnt = 0;cin >> T;while (T--) {++cnt;double x1, x2, y1, y2, l, r;cin >> x1 >> y1 >> x2 >> y2 >> r >> l;double R = (l * sqrt(2)) / 2.0; // 计算圆的半径:对角线长 / 2double d = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)); // 计算两圆圆心距离if (d >= R + r || d + min(R, r) <= max(R, r)) { // 判断两圆是否相交:如果相离或内含,则无交点cout << cnt << ". No problem\n";} else {double part = (d * d + r * r - R * R) / (2 * d); // 计算弦心距 a = (d^2 + r^2 - R^2) / (2d)double ans = 2 * sqrt(r * r - part * part); // 弦长 = 2 * sqrt(r^2 - a^2)cout << cnt << ". " << fixed << setprecision(3) << ans << '\n';}}return 0;
}
AC 记录
