深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)
背景与动机
在前面的策略梯度方法中,演员(Actor)产生的是随机策略 \(\pi_\theta(s)\),即输出动作的概率分布(离散动作)或分布参数(连续动作)。
其优点在于能保证探索:几乎所有动作都有非零概率被采样,避免遗漏潜在高回报动作。
但也带来两个主要缺点:
- 只能同策略(on-policy)训练:评论者提供的 Q 值必须基于当前演员生成的样本,否则会产生高偏差,无法使用经验回放(Replay Buffer)。
- 方差大:即使是同一最优策略,两个回合的回报可能差别很大,导致样本效率低。
相比之下,DQN 这类基于值函数的算法学习的是确定性策略:
行为策略用于探索(如 \(\epsilon\)-greedy),但学习的策略本身是确定性的。
这种方式是 off-policy 的,因此可以使用经验回放并提高样本效率。
DDPG(Deep Deterministic Policy Gradient) 结合了两者的优点:
- 策略梯度(Actor–Critic 架构、可处理连续动作);
- 值函数方法(样本高效、可离策略训练)。
确定性策略梯度定理(Deterministic Policy Gradient Theorem)
定义确定性策略 \(\mu_\theta(s)\),目标函数为:
@Silver2014 推导得其梯度形式为:
这与链式法则一致:
其中:
- \(\nabla_a Q(s,a)\):评论者提供的“方向”,告诉演员如何调整动作;
- \(\nabla_\theta \mu_\theta(s)\):演员内部梯度,指示如何更新参数以产生该动作。
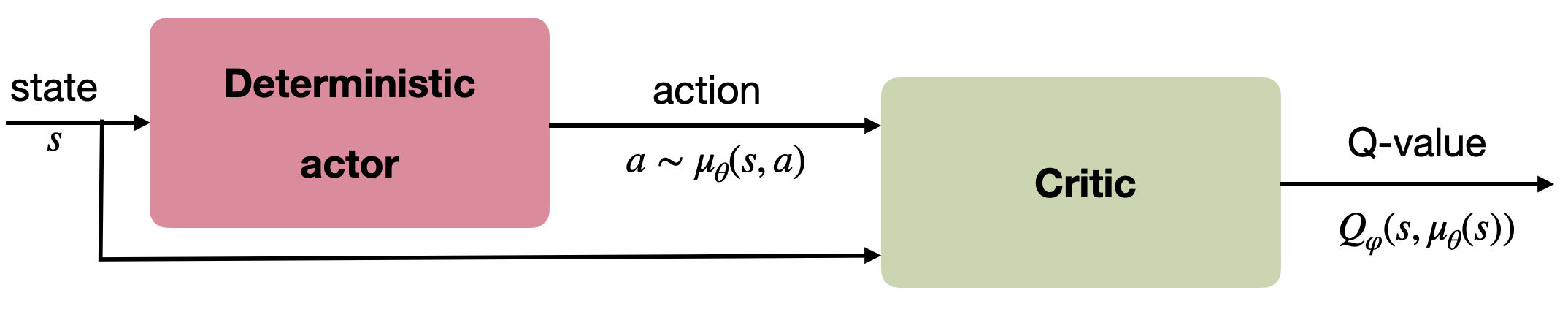
由此自然形成 Actor–Critic 架构:
- Actor:输出确定性动作 \(\mu_\theta(s)\);
- Critic:估计 \(Q_\varphi(s,a)\),并提供 \(\nabla_a Q_\varphi(s,a)\)。
线性逼近器下的 DPG 已验证有效,但非线性函数(深度网络)下最初不稳定。
深度确定性策略梯度(DDPG)
@Lillicrap2015 将 DPG 与 DQN 的思想结合,形成了能在连续动作空间上高效学习的 DDPG 算法。
核心改进
- 经验回放(Replay Buffer):实现离策略训练;
- 目标网络(Target Networks):稳定训练;
- 软更新(Soft Update):缓慢追踪训练网络,减少非平稳性:
网络更新
评论者(Critic)使用 Q-learning 形式的目标:
演员(Actor)使用确定性策略梯度:
探索机制:Ornstein–Uhlenbeck 噪声
由于策略确定性强,探索可能迅速收敛至局部最优。
因此 DDPG 使用加性噪声:
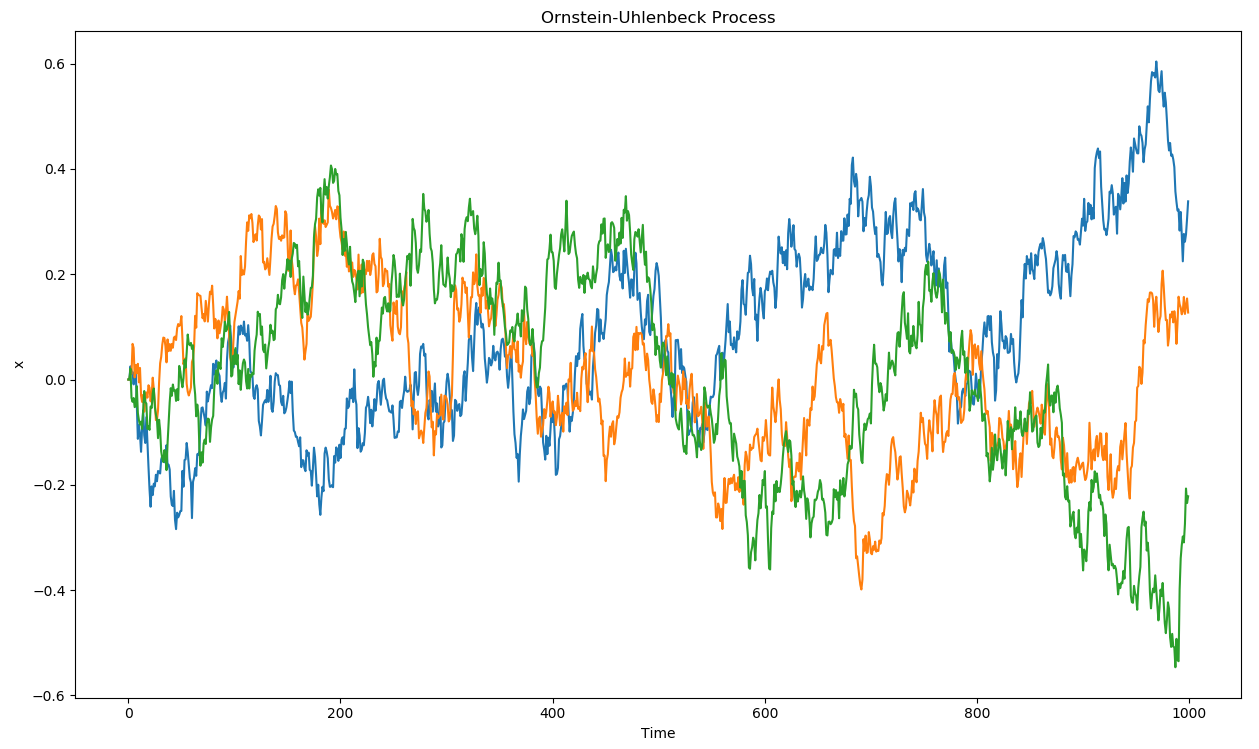
噪声 \(\xi\) 由 Ornstein–Uhlenbeck 过程 生成,具有时间相关性和零均值:
算法流程
DDPG 算法:
- 初始化 Actor \(\mu_\theta\) 与 Critic \(Q_\varphi\);
- 建立对应的目标网络 \(\mu_{\theta'}\)、\(Q_{\varphi'}\);
- 建立经验回放池 \(\mathcal{D}\);
- 对每个 episode:
- 重置噪声过程;
- 对每步 \(t\):
- 执行动作 \(a_t = \mu_\theta(s_t) + \xi\);
- 存储转移 \((s_t,a_t,r_{t+1},s_{t+1})\);
- 随机采样小批量;
- 计算目标值:\[y_k = r_k + \gamma Q_{\varphi'}(s'_k, \mu_{\theta'}(s'_k)) \]
- 更新评论者:\[\mathcal{L} = \frac{1}{N}\sum_k (y_k - Q_\varphi(s_k,a_k))^2 \]
- 更新演员:\[\nabla_\theta J(\theta) = \frac{1}{N}\sum_k \nabla_\theta \mu_\theta(s_k)\nabla_a Q_\varphi(s_k,a)|_{a=\mu_\theta(s_k)} \]
- 软更新目标网络:\[\theta' \leftarrow \tau\theta + (1-\tau)\theta' \\ \varphi' \leftarrow \tau\varphi + (1-\tau)\varphi' \]

特点与局限
- DDPG 为 off-policy 算法:使用旧策略样本更新当前策略;
- 不需要重要性采样(importance sampling);
- 能高效解决连续控制任务;
- 局限:高样本复杂度、对超参数敏感。
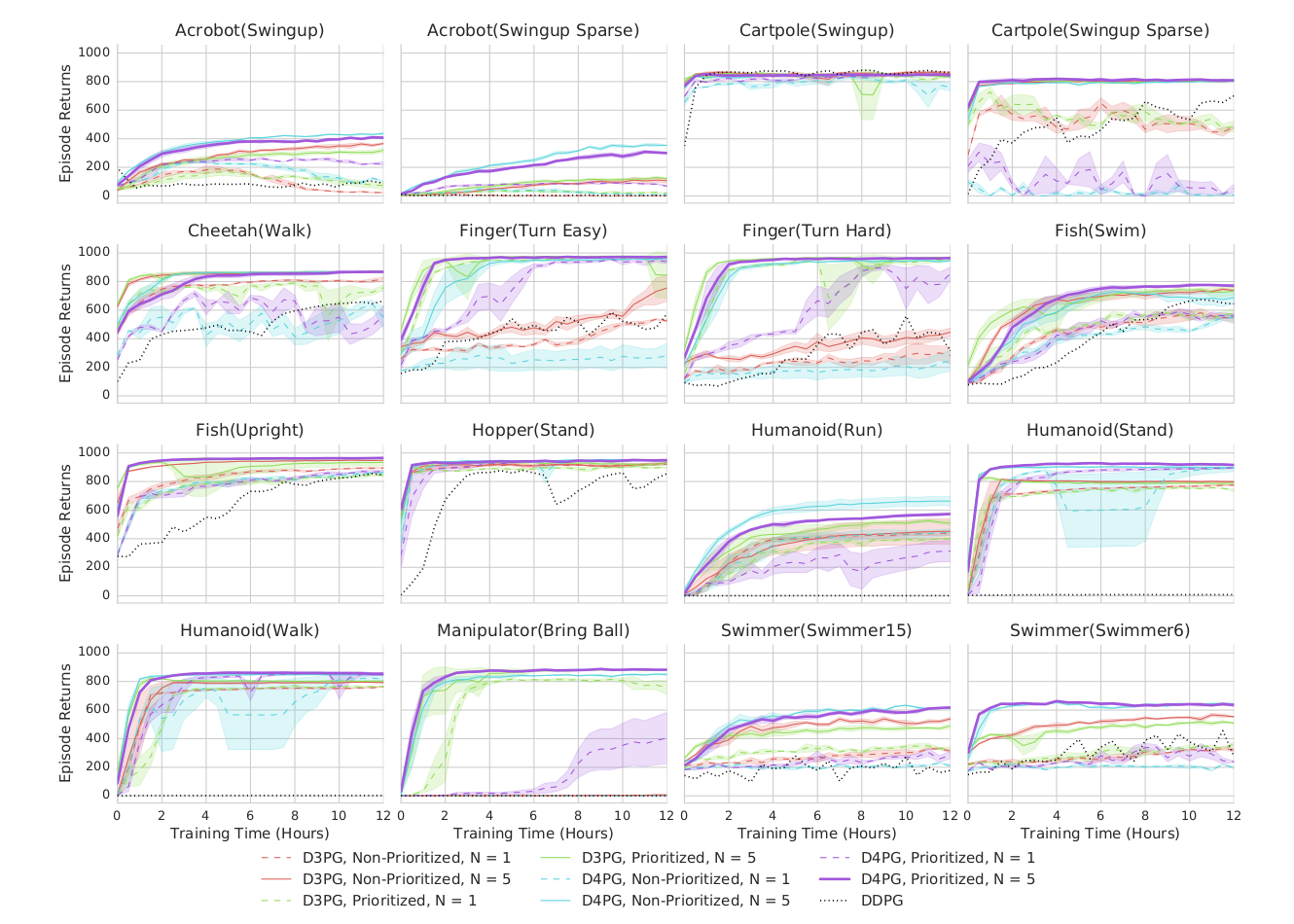
分布式版本(如 @Barth-Maron2018 D4PG)显著提升了训练效率。
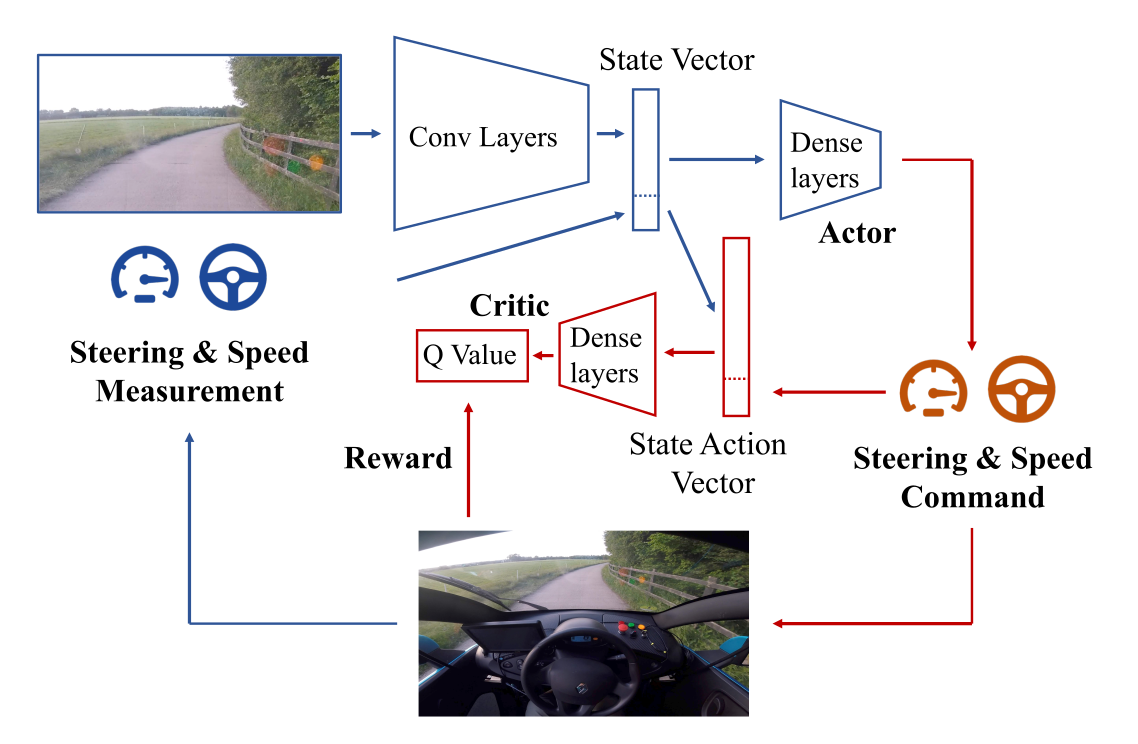
应用示例:自动驾驶
Wayve(2018)展示了基于 DDPG 的“一天学会驾驶”实验。
演员与评论者共享卷积特征层,并采用优先经验回放(PER)。
模型先在仿真环境中调参,再直接在实车(NVIDIA Drive PX2)上训练。
TD3(Twin Delayed Deep Deterministic Policy Gradient)
@Fujimoto2018 提出 TD3,针对 DDPG 的三个主要问题进行改进:
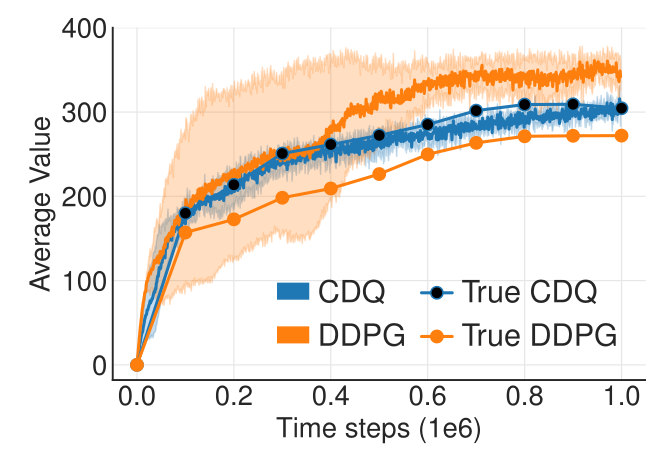
1. Q 值过估计(Clipped Double Q-learning)
DDPG 中的 Bellman 目标:
易因 \(\max\) 操作而过估计。
TD3 使用双评论者:
两者取最小值,减少过估计偏差。
2. 延迟更新演员(Delayed Policy Updates)
Critic 的偏差会污染 Actor 更新。
TD3 每 \(d\) 步才更新一次 Actor,让 Critic 先收敛:
- 每步训练 Critic;
- 每 \(d\) 步训练 Actor 一次。
3. Bellman 目标噪声(Target Policy Smoothing)
为防止过拟合固定动作,TD3 在目标动作中也加噪声:
该技巧保持目标无偏,同时提高泛化。
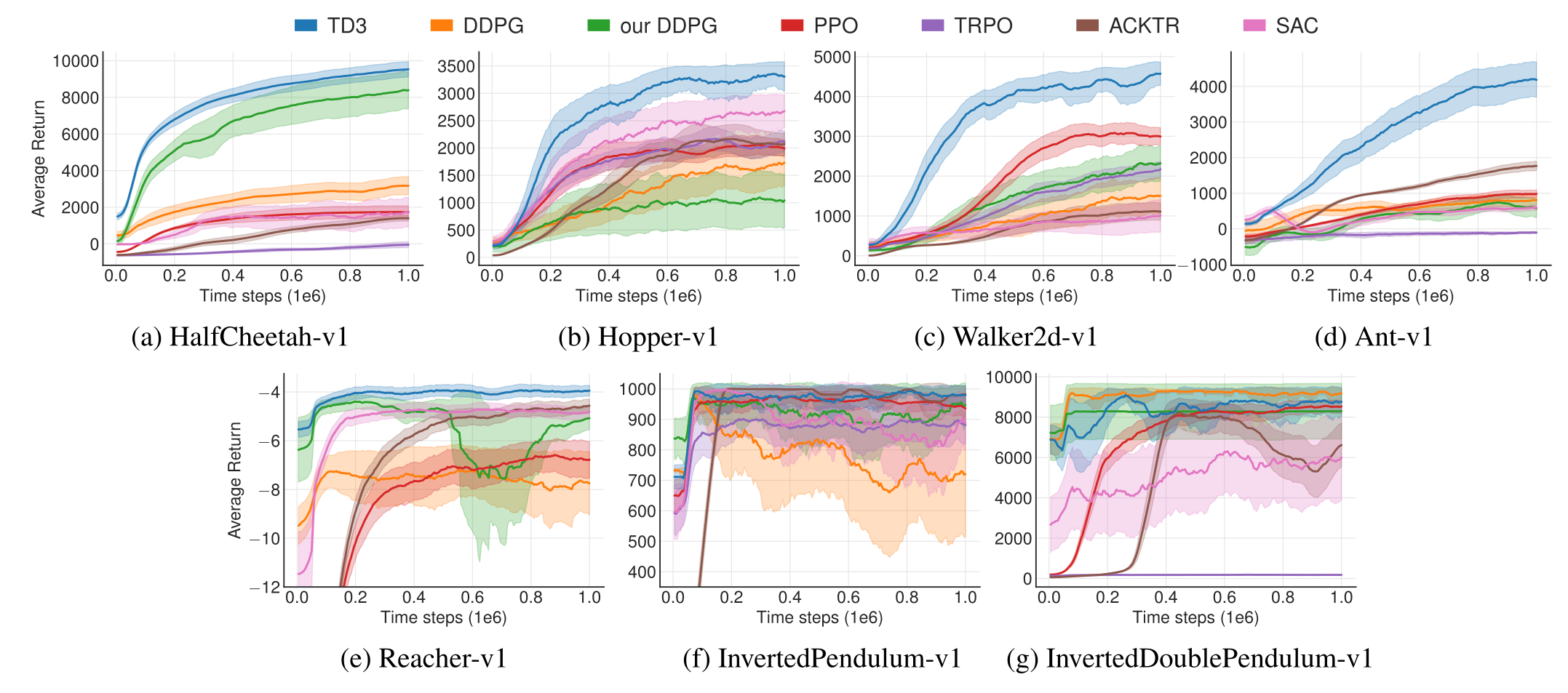
TD3 在连续控制任务上显著优于 DDPG、PPO、SAC 等算法。
D4PG(Distributed Distributional DDPG)
@Barth-Maron2018 提出 D4PG,融合多种先进特性:
| 特性 | 来源 |
|---|---|
| 确定性策略梯度 | DDPG |
| 分布式评论者 \(\mathcal{Z}_\varphi(s,a)\) | Categorical DQN |
| n-step 回报 | A3C |
| 并行执行者(32–64个) | 分布式训练 |
| 优先经验回放(PER) | DQN+PER |
D4PG 能在 CPU 环境下快速收敛并实现高性能,是连续控制中的里程碑算法。