北极通讯网络题解(做题记录)
前言
本文以一道 Kruskal 的好题实例来讲一下 Kruskal 的过程,对于初学 Kruskal 的OIer们有很大的帮助。
luogu 相似题:P1991 无线通讯网。
题目简述
有 n 座村庄,每座村庄的坐标用一对整数 (x,y) 表示。通讯工具分为卫星设备和无线电收发机。
无线电收发机之间通讯的费用为 d ,拥有卫星设备的两座村庄无论相距多远都可以直接通讯。
现在有 k 台卫星设备,请你编一个程序,计算出应该如何分配这 k 台卫星设备,才能使所拥有的无线电收发机的 d 值最小,并保证每两座村庄之间都可以直接或间接地通讯。
例如,对于下面三座村庄:
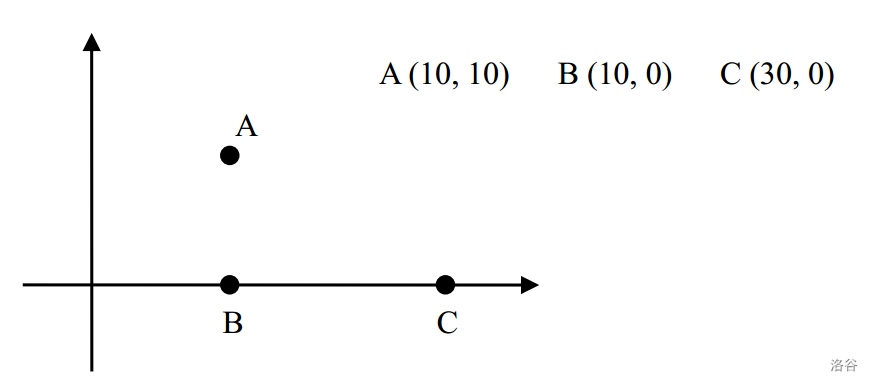
其中 |AB|= 10, |BC|= 20, |AC|= 10 * sqrt{5}≈22.36
如果有 2 台卫星设备 (k=2),则可以把这两台设备分别分配给 B 和 C ,这样最小的 d 可取 10,因为 A 和 B 之间可以用无线电直接通讯;B 和 C 之间可以用卫星直接通讯;A 和 C 可以用 B 中转实现间接通讯。
数据范围
对于全部数据,1≤n≤500,0≤x,y≤10^4 ,0≤k≤100。
思路
PART.1 「显而易见」
显而易见的,本题如果没有卫星设备的话,最小的$d$值就是在刚好保证所有村庄均可以直接或者间接联系的情况下,长度最长的那一条。
注意刚才的内容为“需要「刚好」保证所有村庄均可以直接或者间接联系”,「刚好」可以翻译为,既可以保证村庄之间可以直接或者间接联系的同时还能使每两个村庄之间直接连接的边都尽量的小。那么显然地可以使用 Kruskal 求最小生成树,因为 Kruskal 是对边进行排序,所以绝对能选到边权小的边。
(优美的PART分割线)
PART.2 「算法详解」
Kruskal 算法求的是最小生成树问题。具体操作方式就是,首先对于所有的边进行排序,然后将所有的点分为两类,一类是没有被加入最小生成树的,另一类是已经加入这个最小生成树的。按边权升序进行添加边,并添加对应的点,然后使用并查集统计所有已添加点的状态,当所有的点都被加入这个图之后算法就完成了。如果没有听懂的话点击这里。
PART.3 「基于上面」
基于上面的方法,接下来,再考虑使用 k 个卫星设备的情况,明显地,使用 k 个卫星设备的情况只需要考虑链接 n-k 条边形成的最小生成树,因为对于 n-k 条边,明显可以连接 n-k+1 个点,这样的话,就能保证这个最小生成树内有一台卫星通讯设备,就能与剩下的 k-1 个点使用卫星通讯了。
很显然,我们需要所有的边尽量的小。所以只需要顺着 Kruskal 的正常思路跑一遍,但是只需要跑出 n-k 条边即可。
PART.4 「总而言之」
总而言之,这道题的思路就是 Kruskal 求最小生成树,然后需要加一些预处理,对于每两个点的之间的距离进行计算,直接处理欧拉距离即可。
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=505;
int n,k;
int a[N],b[N];
struct node{int s,e;double leng;
}path[210000];//存储两个点之间的边
int len;
int father[N];double dis(int x,int y){return sqrt((double)(a[x]-a[y])*(a[x]-a[y])+(b[x]-b[y])*(b[x]-b[y]));
}//求两点之间的欧拉距离bool cmp(node x,node y){return x.leng<y.leng;
}/*----------Kruskal----------*/int finding(int i){if(father[i]==i){return i;}father[i]=finding(father[i]);return father[i];
}//寻找最大的祖先bool connect(int st,int ed){int fs=finding(st),fe=finding(ed);if(fs==fe){return false;}father[fs]=fe;return true;
}//在st和ed的最大祖先之间连边void kruskal(){sort(path+1,path+len+1,cmp);//对边排序for(int i=1;i<=n;i++){father[i]=i;}//初始化int cnt=0;for(int i=1;i<=len;i++){if(connect(path[i].s,path[i].e)){cnt++;//如果是刚刚连上的边就证明多通了一个点if(cnt==n-k){ //通了所有的n-k个点就完成了printf("%.2f",path[i].leng);return ;}}}return ;
}/*---------------------------*/int main(){cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i]>>b[i];}for(int i=1;i<n;i++){for(int j=i+1;j<=n;j++){len++;path[len]={i,j,dis(i,j)};}}//枚举任意两个点,建边kruskal();return 0;
}
