P13617 [ICPC 2025 APC] Bit Counting Sequenc
为什么没有题解,我来写一发小清新题解吧。
题意
给你一段 popcount 序列 \(\{a_i\}\),求出它的原序列。
\(n \le 5 \times 10^5\)。
思路
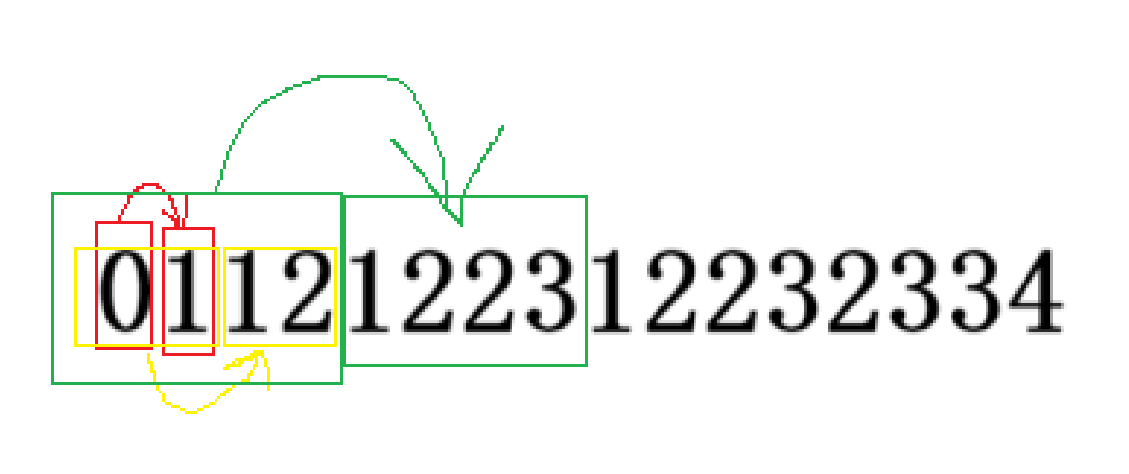
观察一下这个 popcount 序列的性质。(例子的原序列是 [0,15])
对每种颜色的框,右边的框等于左边的框加 \(1\)。
因此你可以认为 popcount 序列是倍增构造的。
本质上是因为,我们把 \([0,2^k-1]\) 原序列的第 \(k\) 位改成 \(1\),就可以造出 \([2^k,2^{k+1}-1]\)。
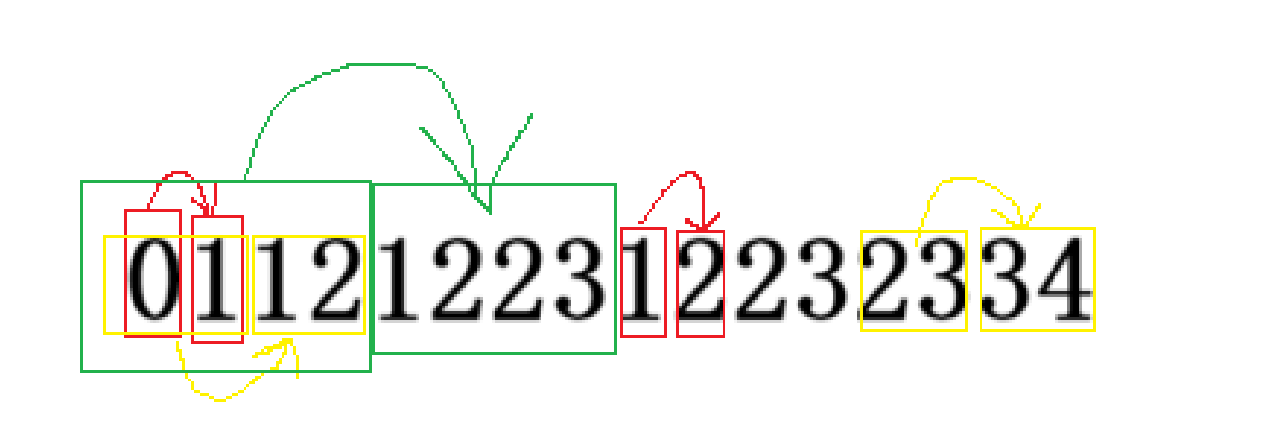
你可以把整个 pop 序列分成若干框框。这里只画其中几个框。
你想知道题目给的 pop 序列是哪一个框框里面的。以此确定原序列。
如果从大框框开始做,先把序列 \(\{a_i\}\) 分到左右两个大框框里面,然后再确定大框框内部是否合法。
如 3 3 4 1 2,先确定出它是 [(0 1 1 2 1 2 2 3 1 2 2 3 2) 3 3 4][1 2 (2 3 2 3 3 4 2 3 3 4 3 4 4 5)]。
然后递归判一下框框内部是不是合法的。比如这里,[... 3 3 4] 和 [1 2 ...] 刚好都是合法的。
但是你咋确定最大的框框,你不知道长度,不知道分割点,只知道左边框框加一等于右边框框而已。
所以我们从小框框开始确定。
还是上面那个例子,你容易确定应该 3 3 一组还是 3 4 一组。
显然是 3 4!因为左边加一等于右边。
然后你有了:[(2) 3][3 4][1 2]。
然后再分组,因为 [(2) 3] + 1 = [3 4]。所以显然它们分一组。
然后你有了下面的完整分组过程:
[(2) 3][3 4][1 2]
[(2) 3 3 4][1 2 (2 3)]
[(1 2 2 3) (2) 3 3 4][1 2 (2 3) (2 3 3 4)]
[(0 1 1 2 1 2 2 3) (1 2 2 3) (2) 3 3 4][1 2 (2 3) (2 3 3 4) (2 3 3 4 3 4 4 5)]
每个框框 [...] 只需要记首位数字。比较框框也只需要比框框的首位数字。(因为框框内部在框框长度更短的时候已经确定合法了,所以只需要比较框框首位大小,类似 SA 的排序)
时间复杂度 \(O(n)\)。
时间复杂度是这么算的:\(n + \frac{n}{2} + \frac{n}{4} + \cdots + 2 + 2 + 2 + \cdots + 2 = O(n)\)。
记得判无解。
只讲了大致思路,还有写细节懒得写了。
code
#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
typedef long long ll;
namespace wing_heart {constexpr int N=5e5+7;int T,n,a[N];bool ans;int st1[N],st2[N];int *vec,*tmp;int svec,stmp;void main() {sf("%d",&T);while(T--) {ans=1;sf("%d",&n);rep(i,1,n) sf("%d",&a[i]);svec=0;vec=st1;tmp=st2;rep(i,1,n) vec[svec++]=a[i];ll pos=0;int t=0;for(;;t++) {if(vec[0]<0) break;if(svec==1) break;stmp=0;if(vec[0]+1!=vec[1]) {pos+=1ll<<t;tmp[stmp++]=vec[0]-1;for(int i=1;i<svec;i+=2) tmp[stmp++]=vec[i];} else {for(int i=0;i<svec;i+=2) tmp[stmp++]=vec[i];}swap(svec,stmp);swap(vec,tmp);}if(vec[0]<0) ans=0;if(!ans) { puts("-1"); continue; }pos+=((1ll<<vec[0])-1)*(1ll<<t);rep(i,1,n) {if(a[i]!=__builtin_popcountll(pos+i-1)) {ans=0;puts("-1");break;}}if(ans) pf("%lld\n",pos);}}
}
int main() {#ifdef LOCALfreopen("in.txt","r",stdin);freopen("my.out","w",stdout);#endifwing_heart :: main();
}
