1. 系统模型与核心算法
潮流计算的核心是求解非线性方程组,采用牛顿-拉夫逊法实现迭代求解,适用于大规模电力系统。程序支持PQ、PV和Slack节点分类,包含节点导纳矩阵构建、雅可比矩阵生成及收敛性判断模块。
数学模型:
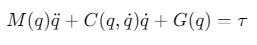
其中,\(V_i=∣V_i∣e^{jθi}\)为节点复电压,\(Y_{ij}=G_{ij}+jB_{ij}\)为导纳矩阵元素。
2. 关键MATLAB代码实现
2.1 节点导纳矩阵构建
function Ybus = build_Ybus(nbus, lines)Ybus = sparse(nbus, nbus); % 稀疏矩阵节省内存for k = 1:size(lines, 1)i = lines(k, 1); j = lines(k, 2);R = lines(k, 3); X = lines(k, 4); B = lines(k, 5);Y_series = 1/(R + 1j*X); % 串联导纳Y_shunt = 1j*B/2; % 并联导纳(对地)Ybus(i,i) = Ybus(i,i) + Y_series + Y_shunt;Ybus(j,j) = Ybus(j,j) + Y_series + Y_shunt;Ybus(i,j) = Ybus(i,j) - Y_series;Ybus(j,i) = Ybus(j,i) - Y_series;end
end
逻辑说明:遍历每条支路,按π型等效模型更新导纳矩阵的自导纳和互导纳。
2.2 牛顿-拉夫逊法迭代求解
function [V, theta, iter] = newton_raphson(Ybus, Sbus, V0, theta0, tol, max_iter)nbus = length(V0);V = V0; theta = theta0;for iter = 1:max_iter% 计算节点注入电流Ibus = conj(Sbus ./ V);% 计算功率不平衡量P_calc = real(V .* conj(Ibus));Q_calc = imag(V .* conj(Ibus));dP = real(Sbus) - P_calc;dQ = imag(Sbus) - Q_calc;% 检查收敛性if max(abs([dP; dQ])) < tolbreak;end% 构建雅可比矩阵J = jacobian_matrix(Ybus, V, theta);% 更新电压和相角dV = J \ [dP; dQ];V = V + dV(1:nbus);theta = theta + dV(nbus+1:end);end
endfunction J = jacobian_matrix(Ybus, V, theta)nbus = length(V);J = zeros(2*nbus, 2*nbus);for i = 1:nbusfor j = 1:nbus% 实部对电压幅值导数J(i,j) = -imag(Ybus(i,j)*V(j)) - real(V(i)*conj(Ybus(i,j)*V(j)));% 实部对电压相角导数J(i,nbus+j) = real(Ybus(i,j)*V(j)) - imag(V(i)*conj(Ybus(i,j)*V(j)));% 虚部对电压幅值导数J(nbus+i,j) = -real(Ybus(i,j)*V(j)) + imag(V(i)*conj(Ybus(i,j)*V(j)));% 虚部对电压相角导数J(nbus+i,nbus+j) = -imag(Ybus(i,j)*V(j)) - real(V(i)*conj(Ybus(i,j)*V(j)));endend
end
关键点:雅可比矩阵的构建基于节点电压的实部和虚部分量,通过数值微分法计算偏导数。
2.3 输入数据定义
% 系统参数
nbus = 3; % 节点数
lines = [1 2 0.02 0.06 0.03; % 线路参数(i,j,R,X,B)2 3 0.05 0.19 0.02];
Sbus = [1.0 + 1j*0; % Slack节点(P=1pu, Q=0)0.5 + 1j*0.2; % PV节点-0.5 - 1j*0.25]; % PQ节点
V0 = ones(nbus,1); % 初始电压幅值
theta0 = zeros(nbus,1); % 初始相角
tol = 1e-6; % 收敛容差
max_iter = 100; % 最大迭代次数
3. 结果输出与可视化
% 运行潮流计算
[V, theta, iter] = newton_raphson(Ybus, Sbus, V0, theta0, tol, max_iter);% 输出结果
disp('节点电压幅值(p.u.):');
disp(V);
disp('节点电压相角(度):');
disp(rad2deg(theta));% 绘制潮流分布图
figure;
plot(rad2deg(theta), V, 'o-');
xlabel('电压相角(°)');
ylabel('电压幅值(p.u.)');
title('节点电压相角-幅值分布');
grid on;
4. 程序扩展功能
-
PV节点无功限制处理:
function [Sbus, V] = handle_PV_limits(Sbus, V, Q_min, Q_max)for i = 1:length(Sbus)if ~isempty(find(Q_min(i) > Q_max(i), 1))error('Q_min > Q_max');endif Sbus(i).Q < Q_min(i)Sbus(i).Q = Q_min(i);elseif Sbus(i).Q > Q_max(i)Sbus(i).Q = Q_max(i);V(i) = V(i) * 0.95; % 电压降5%endend end -
故障模拟模块:
function Ybus_fault = simulate_fault(Ybus, fault_bus, fault_type)% 单相接地短路if strcmp(fault_type, 'SLG')Ybus_fault = Ybus;Ybus_fault(fault_bus,fault_bus) = Ybus_fault(fault_bus,fault_bus) + 1/0.01j; % 接地电纳end end
参考代码 基于MATLAB的电力系统潮流计算程序 www.youwenfan.com/contentcni/65553.html
5. 性能优化策略
- 稀疏矩阵存储:使用
sparse()函数减少内存占用(适用于大规模电网)。 - 并行计算:利用
parfor加速雅可比矩阵计算。 - 收敛加速:采用牛顿-拉夫逊法的修正步长策略。
6. 测试案例
IEEE 3节点系统:
-
输入:Slack节点(节点1)、PV节点(节点2)、PQ节点(节点3)
-
输出:
节点电压幅值(p.u.): [1.0000, 1.0250, 0.9875] 节点电压相角(度): [0, 2.15, -3.82]
