当前位置：首页 > news >正文

ZKW线段树

news 2025/10/23 21:00:17

ZKW线段树

线段树，一种实用的数据结构，但它有以下弊端。
1)常数大
2)码量大
zkw线段树是由张昆玮发明的的非递归式线段树写法。因为其非递归的写法，所以具有常数极小，码量小的特点。

ZKW线段树的思想：

与普通线段树的维护目标一致（节点维护区间信息）
但ZKW的维护方式与普通线段树有较大区别。

ZKW线段树与普通线段树：

可以看出，普通线段树的有效节点以完全二叉树的形式存储。ZKW线段树的有效节点被集中在叶子结点处。两种线段树的都需要4倍空间

ZKW线段树的形式：

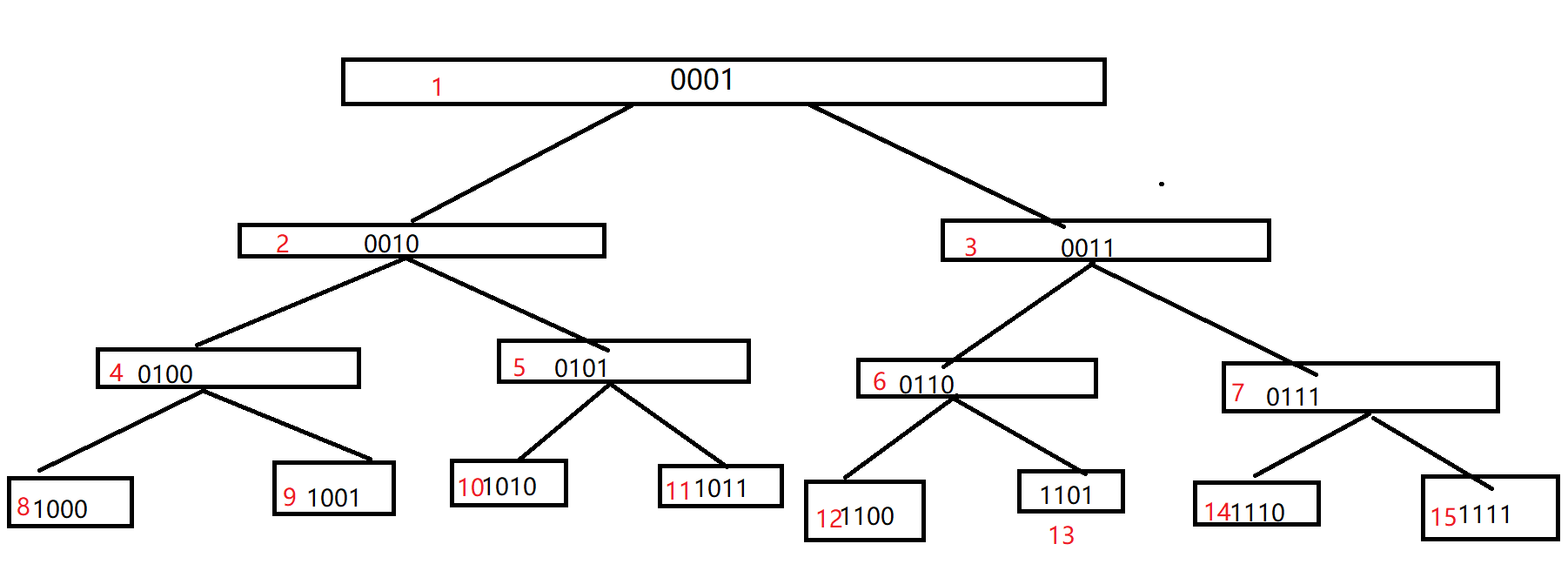
可以发现，ZKW线段树与普通线段树使用的都是“堆式存储法”，即左儿子的结点编号是父节点编号的左移一位，右儿子则在左儿子的基础上加1，这种存储法的好处会在建树，修改，查询中体现

ZKW线段树的建立：

首先我们会维护一个m值（非叶结点数），令m大于n（要维护的叶子节点总数）。保证这棵树的叶子足够容纳要维护的值
然后要从m倒推回到1号结点，像普通线段树建树时维护结点信息一样，保证在维护到每个节点时该节点的孩子都已维护完。

代码实现：

我们维护了区间和，区间最小值，区间最大值

点击查看代码

inline void build(){for(m=1;m<=n;m<<=1);for(int i=m+1;i<=n+m;i++)t[i]=mx[i]=mn[i]=read();for(int i=m-1;i;i--){t[i]=t[ls]+t[rs];mn[i]=min(mn[ls],mn[rs]);mx[i]=max(mx[ls],mx[rs]);}
}

注意，这里的mn,与mx的处理是在无修改操作的基础上实行的。带修改的代码如下（类似于差分思想？）：

点击查看代码

inline void build(){for(m=1;m<=n;m<<=1);for(int i=m+1;i<=n+m;i++)t[i]=mx[i]=mn[i]=read();for(int i=m-1;i;i--){t[i]=t[ls]+t[rs];mn[i]=min(mn[ls],mn[rs]);mn[ls]-=mn[i],mn[rs]-=mn[i];mx[i]=max(mx[ls],mx[rs]);mx[ls]-=mx[i],mx[rs]-=mx[i];}
}

同时，以下所有的代码都基于带修改版本

ZKW线段树的修改（更新）：

单点修改：

只需找到对应的叶结点，沿着父亲一路向上更新即可

代码实现：

点击查看代码

inline void upd_node(int pos,int d,int ans=0){pos+=m,mx[pos]+=d,mn[pos]+=d,t[pos]+=d;for(;pos>1;pos>>=1){t[pos]+=d;ans=min(mn[pos],mn[pos^1]);mn[pos]-=ans,mn[pos^1]-=ans,mn[pos>>1]+=ans;ans=max(mx[pos],mx[pos^1]);mx[pos]-=ans,mx[pos^1]-=ans,mx[pos>>1]+=ans;}
}

这里假设我们将结点的值增加d。

区间更新：

ZKW线段树的区间修改比较难理解。
我们发现，非递归的ZKW无法直接来到要更新的区间进行修改。
我们不妨令左端点L-1,右端点R+1。
我们就可以保证，L与R一定不在要修改的区间上，并且L处于要修改的区间的左端点左邻，R处于要修改的区间的右端点右邻。
有性质：L的右边（右儿子）一定是要修改的区间，R的左边（左儿子）一定是要修改的区间。
所以实现呼之欲出：
我们令左端点L-1,右端点R+1。
在更新权值时，判断左端点所处的区间是否是它父节点的左儿子（即判断右儿子的存在性），是的话就让该节点的兄弟得到更新。
对右端点的处理同理，判断右端点所处的区间是否是父节点的右儿子，是的话让兄弟得到更新。
终止条件：左端点与右端点成为兄弟结点（左右端点间无区间可更新了）
过程如图：

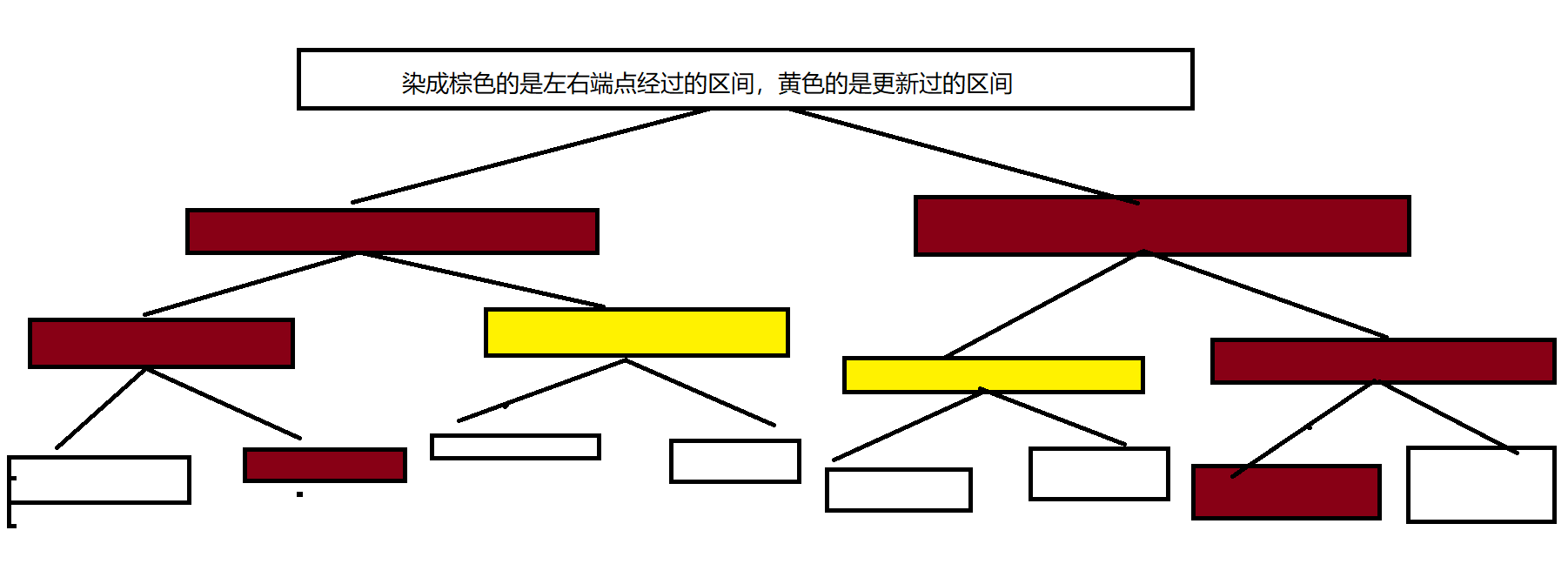
可以看到被更新的区间都被染成黄色了，但ZKW是没有标记下传一说的。
如果我们要查询的区间在黄色去区间的子树内怎么办？
易得”标记永久化“
因为我们已经将一个节点的标记永久化了，所以在该结点被访问时直接将标记值与该节点所管辖区间的长度操作即可。

区间更新的特殊情况：

注意到，我们在更新时会将右端点R+1。
如果R+1后越过了总区间[1,n]的右端点会不会产生错误？
实际是不会的，因为若右端点R+1后越出[1,n]，这代表了原本的R就是n，即为整个[L,n]区间都是要更新的，而R越出[1,n]与L对右儿子进行的操作没有影响。
（或者说L,R存在的价值就是约束左右端点对兄弟节点的更新范围，既然R=n,则整个右区间是无约束的，此时R的存在就没有价值了）

代码实现：

点击查看代码

inline void upd_part(ll L,ll R,ll d){ll ans=0,lc=0,rc=0,len=1;for(L+=m-1,R+=m+1;L^R^1;L>>=1,R>>=1,len<<=1){if(L&1^1) add[L^1]+=d,lc+=len,mn[L^1]+=d,mx[L^1]+=d;if(R&1) add[R^1]+=d,rc+=len,mn[R^1]+=d,mx[R^1]+=d;t[L>>1]+=d*lc,t[R>>1]+=d*rc;ans=min(mn[L],mn[L^1]),mn[L]-=ans,mn[L^1]-=ans,mn[L>>1]+=ans;ans=min(mn[R],mn[R^1]),mn[R]-=ans,mn[R^1]-=ans,mn[R>>1]+=ans;ans=max(mx[L],mx[L^1]),mx[L]-=ans,mx[L^1]-=ans,mx[L>>1]+=ans;ans=max(mx[R],mx[R^1]),mx[R]-=ans,mx[R^1]-=ans,mx[R>>1]+=ans;}for(lc+=rc,L>>=1;L;L>>=1){t[L]+=d*lc;ans=min(mn[L],mn[L^1]),mn[L]-=ans,mn[L^1]-=ans,mn[L>>1]+=ans;ans=max(mx[L],mx[L^1]),mx[L]-=ans,mx[L^1]-=ans,mx[L>>1]+=ans;}
}

其中lc表示左端点所处的节点在更新区间范围内的长度，rc同理。

zkw线段树的查询:

单点查询：

从叶子节点一直往上跳到父节点，把路径中的信息收集起来即可。

代码实现：

点击查看代码

inline int que_node(int pos,int ans=0){for(pos+=m;pos;pos>>=1) ans+=mn[pos];return ans;
}

区间查询：

与区间更新的思路差不多。
但它与普通线段树的区别在于普通线段树是自上而下查询再自下而上递归。
所以ZKW线段树的查询对于标记无法释放。
我们再查询区间内直接将标记与区间长度操作即可

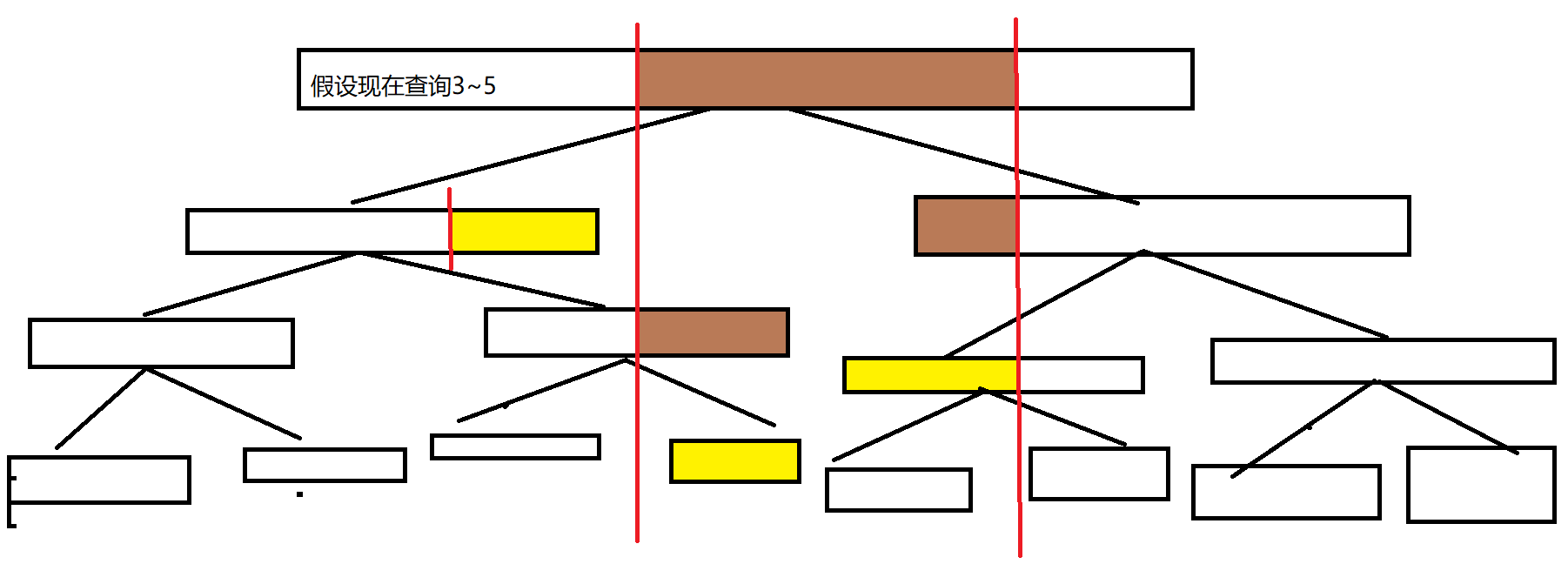
代码实现：

点击查看代码

inline ll que_sum(ll L,ll R){ll lc=0,rc=0,len=1,ans=0;for(L+=m-1,R+=m+1;L^R^1;L>>=1,R>>=1,len<<=1){if(L&1^1) ans+=t[L^1]+len*add[L^1],lc+=len;if(R&1) ans+=t[R^1]+len*add[R^1],rc+=len;if(add[L>>1]) ans+=add[L>>1]*lc;if(add[R>>1]) ans+=add[R>>1]*rc;}for(lc+=rc,L>>=1;L;L>>=1) if(add[L]) ans+=add[L]*lc;return ans;
}
inline int que_min(int L,int R,int l=0,int r=0,int ans=0){if(L==R) return que_node(L);for(L+=m,R+=m;L^R^1;L>>=1,R>>=1){l+=mn[L],r+=mn[R];if(L&1^1) l=min((ll)l,mn[L^1]);if(R&1) r=min((ll)r,mn[R^1]);}for(ans=min(l,r),L>>=1;L;L>>=1) ans+=mn[L];return ans;
}
inline int que_max(int L,int R,int l=0,int r=0,int ans=0){if(L==R) return que_node(L);for(L+=m,R+=m;L^R^1;L>>=1,R>>=1){l+=mx[L],r+=mx[R];if(L&1^1) l=max((ll)l,mx[L^1]);if(R&1) r=max((ll)r,mx[R^1]);}for(ans=max(l,r),L>>=1;L;L>>=1) ans+=mx[L];return ans;
}

注意查询时不能干涉到不相干的节点。
当L=R时要特判，防止陷入死循环

ZKW的完整代码实现：

点击查看代码

#include<bits/stdc++.h>
#include<cstdio>
#define ll long long
using namespace std;
//#define getchar() {p1==p2&&(p2=(pq=buf)+fread(buf,1,1<<21,stdin),pq==p2)?EOF:*p1++}
char buf[1<<21],*p1=buf,*p2=buf;
inline ll read(){char ch=getchar();ll k=0,f=1;while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}while(isdigit(ch)) {k=k*10+ch-'0';ch=getchar();}return k*f;
}
char sr[1<<21],z[20];
int C=-1,Z;
inline void Ot() {fwrite(sr,1,C+1,stdout),C=-1;}
inline void print(ll x){if(C>1<<20) Ot();if(x<0) sr[++C]=45,x=-x;while(z[++Z]=x%10+48,x/=10);while(sr[++C]=z[Z],--Z);sr[++C]='\n';
}
ll m,n,q;
const int N=1e5+7;
ll t[N<<2],add[N<<2];
ll mx[N<<2],mn[N<<2]; 
#define ls (i<<1)
#define rs (i<<1|1)
inline void build(){for(m=1;m<=n;m<<=1);for(int i=m+1;i<=n+m;i++)t[i]=mx[i]=mn[i]=read();for(int i=m-1;i;i--){t[i]=t[ls]+t[rs];mn[i]=min(mn[ls],mn[rs]);mn[ls]-=mn[i],mn[rs]-=mn[i];mx[i]=max(mx[ls],mx[rs]);mx[ls]-=mx[i],mx[rs]-=mx[i];}
}
inline void upd_node(int pos,int d,int ans=0){pos+=m,mx[pos]+=d,mn[pos]+=d,t[pos]+=d;for(;pos>1;pos>>=1){t[pos]+=d;ans=min(mn[pos],mn[pos^1]);mn[pos]-=ans,mn[pos^1]-=ans,mn[pos>>1]+=ans;ans=max(mx[pos],mx[pos^1]);mx[pos]-=ans,mx[pos^1]-=ans,mx[pos>>1]+=ans;}
}
inline void upd_part(ll L,ll R,ll d){ll ans=0,lc=0,rc=0,len=1;for(L+=m-1,R+=m+1;L^R^1;L>>=1,R>>=1,len<<=1){if(L&1^1) add[L^1]+=d,lc+=len,mn[L^1]+=d,mx[L^1]+=d;if(R&1) add[R^1]+=d,rc+=len,mn[R^1]+=d,mx[R^1]+=d;t[L>>1]+=d*lc,t[R>>1]+=d*rc;ans=min(mn[L],mn[L^1]),mn[L]-=ans,mn[L^1]-=ans,mn[L>>1]+=ans;ans=min(mn[R],mn[R^1]),mn[R]-=ans,mn[R^1]-=ans,mn[R>>1]+=ans;ans=max(mx[L],mx[L^1]),mx[L]-=ans,mx[L^1]-=ans,mx[L>>1]+=ans;ans=max(mx[R],mx[R^1]),mx[R]-=ans,mx[R^1]-=ans,mx[R>>1]+=ans;}for(lc+=rc,L>>=1;L;L>>=1){t[L]+=d*lc;ans=min(mn[L],mn[L^1]),mn[L]-=ans,mn[L^1]-=ans,mn[L>>1]+=ans;ans=max(mx[L],mx[L^1]),mx[L]-=ans,mx[L^1]-=ans,mx[L>>1]+=ans;}
}
inline int que_node(int pos,int ans=0){for(pos+=m;pos;pos>>=1) ans+=mn[pos];return ans;
}
inline ll que_sum(ll L,ll R){ll lc=0,rc=0,len=1,ans=0;for(L+=m-1,R+=m+1;L^R^1;L>>=1,R>>=1,len<<=1){if(L&1^1) ans+=t[L^1]+len*add[L^1],lc+=len;if(R&1) ans+=t[R^1]+len*add[R^1],rc+=len;if(add[L>>1]) ans+=add[L>>1]*lc;if(add[R>>1]) ans+=add[R>>1]*rc;}for(lc+=rc,L>>=1;L;L>>=1) if(add[L]) ans+=add[L]*lc;return ans;
}
inline int que_min(int L,int R,int l=0,int r=0,int ans=0){if(L==R) return que_node(L);for(L+=m,R+=m;L^R^1;L>>=1,R>>=1){l+=mn[L],r+=mn[R];if(L&1^1) l=min((ll)l,mn[L^1]);if(R&1) r=min((ll)r,mn[R^1]);}for(ans=min(l,r),L>>=1;L;L>>=1) ans+=mn[L];return ans;
}
inline int que_max(int L,int R,int l=0,int r=0,int ans=0){if(L==R) return que_node(L);for(L+=m,R+=m;L^R^1;L>>=1,R>>=1){l+=mx[L],r+=mx[R];if(L&1^1) l=max((ll)l,mx[L^1]);if(R&1) r=max((ll)r,mx[R^1]);}for(ans=max(l,r),L>>=1;L;L>>=1) ans+=mx[L];return ans;
}
signed main(){return 0;
}

完结撒花！！！
参考文献：https://www.cnblogs.com/Judge/p/9514862.html

查看全文

http://www.hskmm.com/?act=detail&tid=37621