下面的机器数都以16进制表示
| w | func1(w) | func2(w) |
|---|---|---|
| 机器数 ; 值 | 机器数 ; 值 | 机器数 ; 值 |
| 0000007F;127 | 0000007F;127 | 0000007F;127 |
| 00000080;128 | 00000080;128 | FFFFFF80;-128 |
| 000000FF;255 | 000000FF;255 | FFFFFFFF;-1 |
| 00000100;256 | 00000000;0 | 00000000;0 |
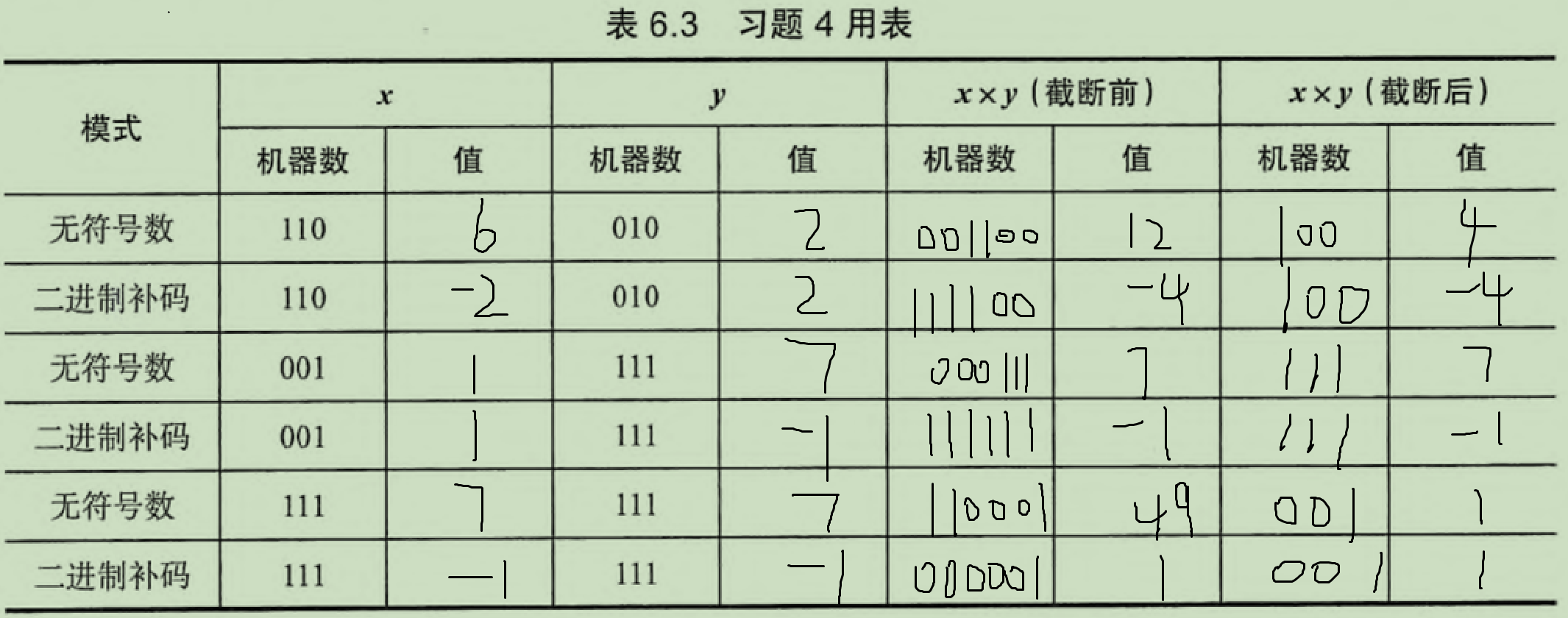
两个函数的功能:都是先将参数左移24位之后再右移24位;区别是func1是先移动完了再强制转换,所以全程都是无符号数,采用逻辑右移;而func2左移完了之后先转换再右移,所以采用算数右移
4.
5.
通过分析反编译的代码可以发现x扩大了15倍,所以M为15;而y+=3的原因是为了向0取整,根据y>>=2可以得出N=4
6.
串行进位:
\[C_1 = A_1 C_0 + B_1 C_0 + A_1 B_1
\]
\[C_2 = A_2 C_1 + B_2 C_1 + A_2 B_2
\]
\[C_3 = A_3 C_2 + B_3 C_2 + A_3 B_3
\]
\[C_4 = A_4 C_3 + B_4 C_3 + A_4 B_4
\]
并行进位:
\[C_1 = A_1 B_1 + (A_1 + B_1) C_0
\]
\[C_2 = A_2 B_2 + (A_2 + B_2) A_1 B_1 + (A_2 + B_2)(A_1 + B_1) C_0
\]
\[C_3 = A_3 B_3 + (A_3 + B_3) A_2 B_2 + (A_3 + B_3)(A_2 + B_2) A_1 B_1 + (A_3 + B_3)(A_2 + B_2)(A_1 + B_1) C_0
\]
\[C_4 = A_4 B_4 + (A_4 + B_4) A_3 B_3 + (A_4 + B_4)(A_3 + B_3) A_2 B_2 + (A_4 + B_4)(A_3 + B_3)(A_2 + B_2) A_1 B_1 + (A_4 + B_4)(A_3 + B_3)(A_2 + B_2)(A_1 + B_1) C_0
\]
(1). 由题\([x+y]_{\text{补}}=0010,[x-y]_{\text{补}}=1000\),所以\(x+y=2,x-y=-8\)(溢出)
(2).
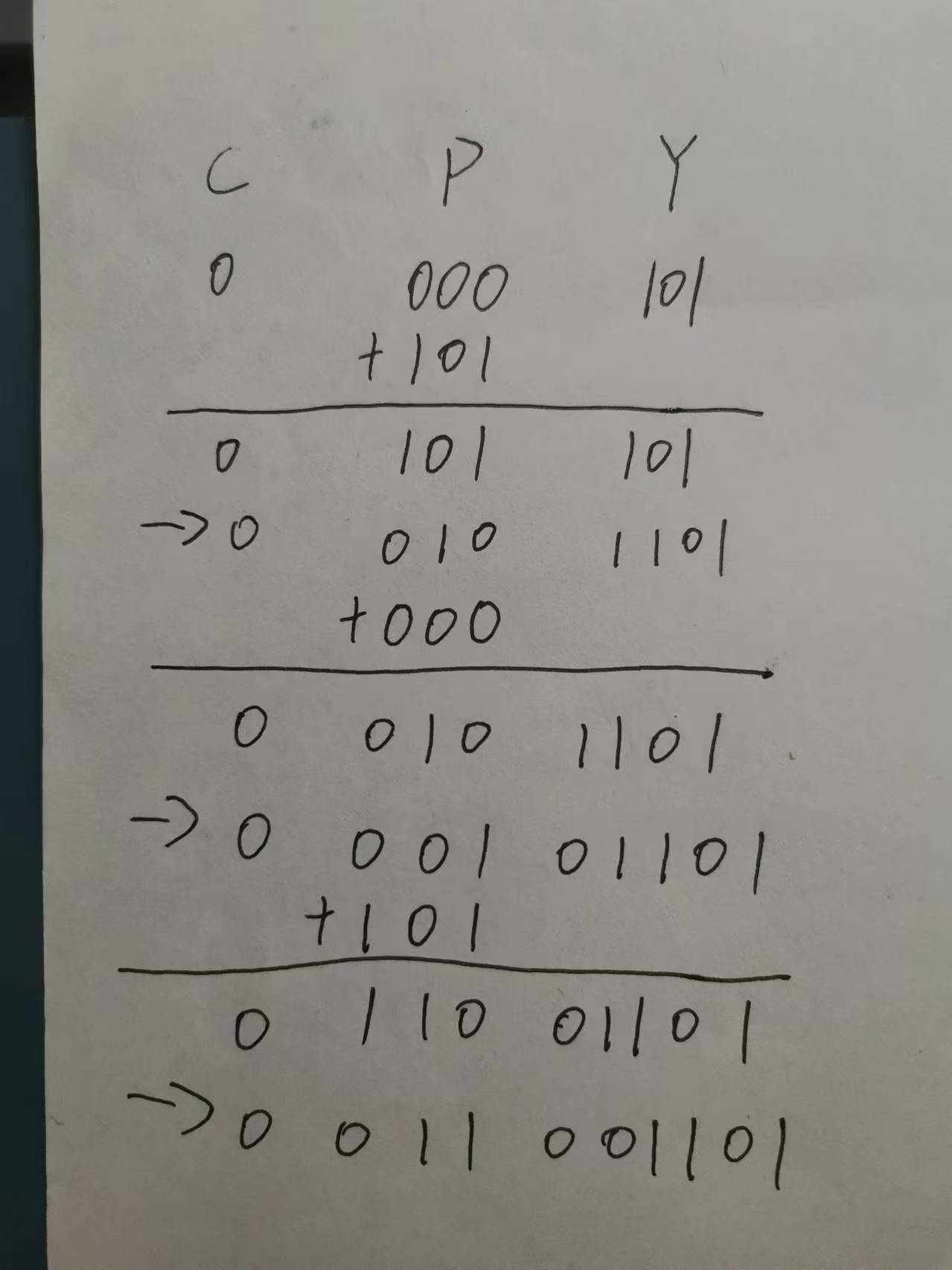
符号位单独处理,可以知道为1,所以最后的原码结果为\(10011001\),真值为\(-25\);由于\(P\)是一个非0数,所以溢出
(3).
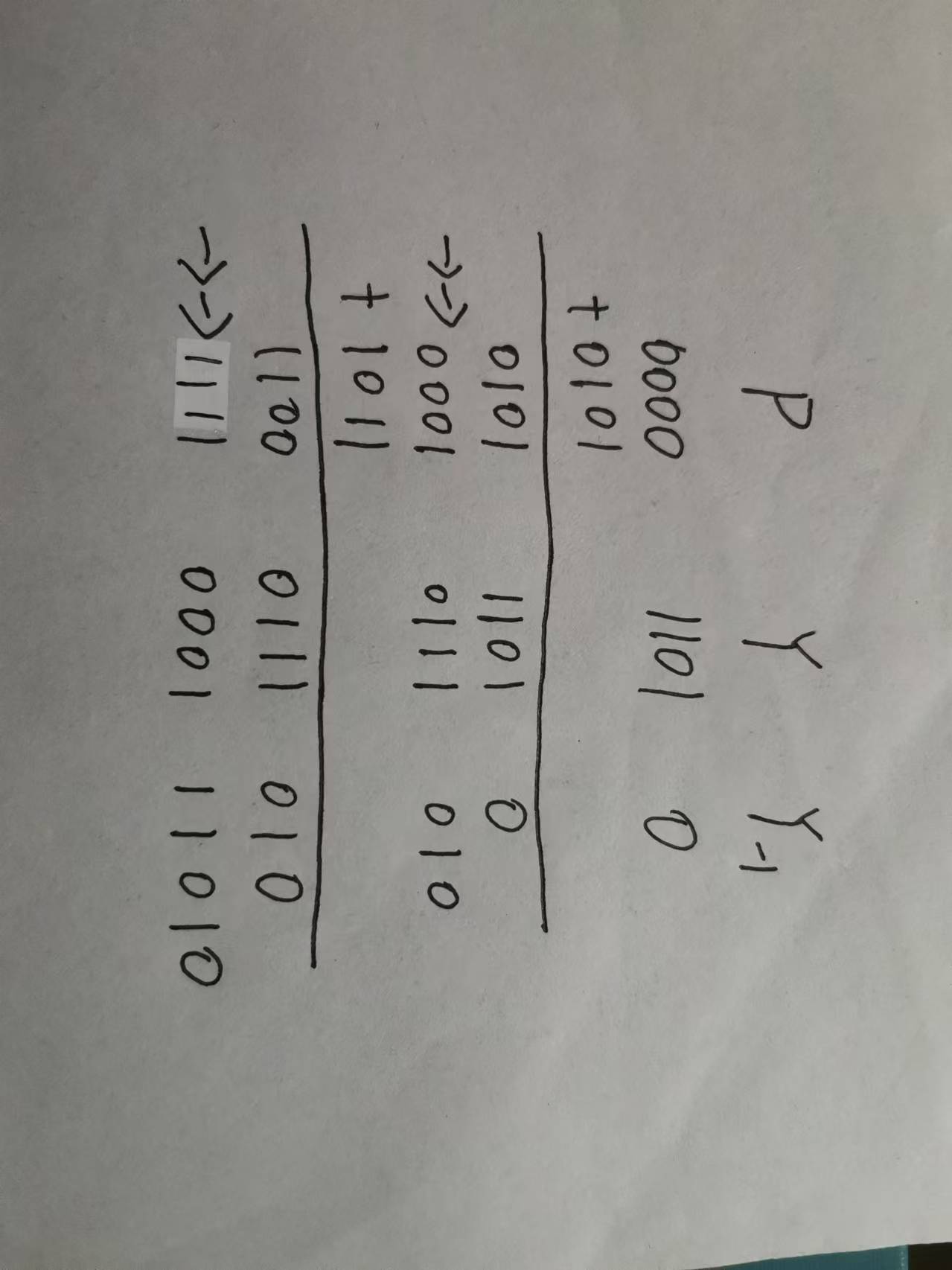
可以得到最后的补码结果为\(11110001\),真值为\(-15\)
(4).
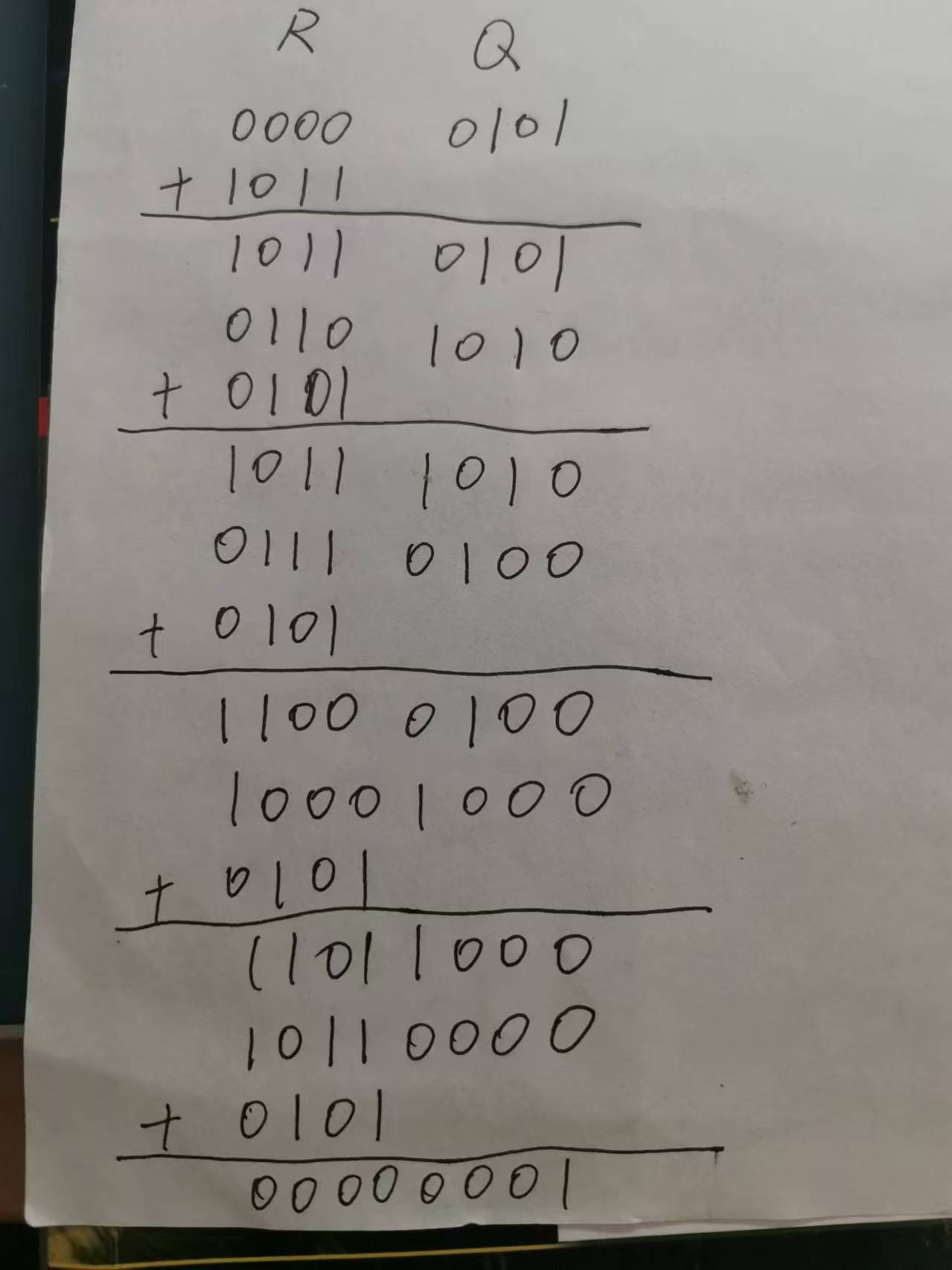
符号单独处理,可以得到结果为商为-1余为0
(5).

最后修正商,可得商为1111,真值为-1;不用修正余数,为0010,真值为2
11
(4).
x = (15/16) × 2⁵,y = (2/16) × 2⁷。运算为 x - y
- 将 x 和 y 表示为规定的浮点数格式
- x
- 尾数: 15/16 = (0.1111)₂。其 6 位补码表示为
00.1111 - 阶码: 5。其 4 位移码表示为 5 + 8 = 13 = (1101)₂
- 所以,x =
1101,001111
- 尾数: 15/16 = (0.1111)₂。其 6 位补码表示为
- y
- 尾数: 2/16 = 1/8 = (0.001)₂。其 6 位补码表示为
00.0010 - 阶码: 7。其 4 位移码表示为 7 + 8 = 15 = (1111)₂
- 所以,y =
1111,000010
- 尾数: 2/16 = 1/8 = (0.001)₂。其 6 位补码表示为
- x
接下来,需要对阶,使两个数的阶码相等。选择较大的阶码 7 作为公共阶码。x 的阶码需要从 5 调整到 7,因此 x 的尾数需要右移 2 位
- 情况一:不采用任何附加位
-
对阶:
- x 的尾数
00.1111右移 2 位 - 移位后,x 的尾数变为
00.0011(最后两位11丢失) - x 的阶码变为 7
- x 的尾数
-
尾数相加:
00.0011(x 的尾数) +11.1110(-y 的尾数) =00.0001
-
规格化:
- 结果
00.0001的符号位与最高数值位不同,需要规格化 - 尾数左移 3 位变为
00.1000 - 阶码相应地减 3,即 7 - 3 = 4
- 结果
-
得出结果:
- 规格化后的尾数为
00.1000,阶码为 4 - 其值为: (0.1000)₂ × 2⁴ = (1/2) × 16 = 8
- 规格化后的尾数为
-
计算结果为 8
-
情况二:采用 2 位附加位 (保护位 G,舍入位 R)
-
对阶:
- x 的尾数
00.1111附加两位00,变为00.1111 00 - 右移 2 位后,尾数部分变为
00.0011,保护位 G = 1,舍入位 R = 1
- x 的尾数
-
尾数相加:
- 将 x 的对阶后尾数与 -y 的尾数相加 (运算时包含附加位):
00.0011 11 + 11.1110 00 -----------------00.0001 11 - 结果的尾数部分为
00.0001,G = 1,R = 1。阶码为 7
- 将 x 的对阶后尾数与 -y 的尾数相加 (运算时包含附加位):
-
规格化:
- 结果
00.0001 11需要规格化 - 尾数左移 3 位,变为
00.1110 00 - 阶码相应地减 3,即 7 - 3 = 4
- 规格化后,尾数为
00.1110,G = 0,R = 0
- 结果
-
舍入:
- 根据“就近舍入到偶数”规则,检查 G、R 和 S (粘位,此处为0) 的值
- 由于 G=0,表示移出的值小于最低有效位的一半,因此执行向下舍入 (即截断)
- 舍入后的尾数仍为
00.1110
-
得出结果:
- 最终尾数为
00.1110,阶码为 4 - 其值为: (0.1110)₂ × 2⁴ = (1/2 + 1/4 + 1/8) × 16 = (7/8) × 16 = 14
- 最终尾数为
-
计算结果为 14
