题目描述
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:
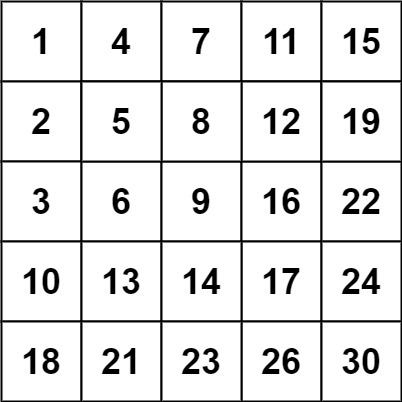
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-109 <= target <= 109
解法一
思路:

对矩阵按照中心点进行分割,分成四个小的矩阵,在设置一个堆栈,堆栈每个元素是一个四维数组,记录矩阵左上角坐标和右下角坐标。
如果target=matrix[rmiddle][cmiddle],则找到
如果target>matrix[rmiddle][cmiddle],则2,3,4子矩阵进入堆栈
如果target<matrix[rmiddle][cmiddle],则1,2,3子矩阵进入堆栈
代码:
class Solution {public boolean searchMatrix(int[][] matrix, int target) {Deque<int[]> stack = new ArrayDeque<>();int m = matrix.length, n = matrix[0].length;int leftRow=0, leftCol=0, rightRow=m-1, rightCol=n-1;int[] left2right={leftRow,leftCol,rightRow,rightCol};stack.push(left2right);while(!stack.isEmpty()) {//入栈问题int[] left2left = stack.pop();leftRow = left2left[0];leftCol = left2left[1];rightRow = left2left[2];rightCol = left2left[3];int rowMiddle = (leftRow + rightRow) / 2, colMiddle = (leftCol + rightCol) / 2;if (matrix[rowMiddle][colMiddle] == target) {return true;} else if (leftRow >= rightRow && leftCol >= rightCol) continue;else if (target < matrix[rowMiddle][colMiddle]) {stack.push(new int[]{leftRow, leftCol, rowMiddle, colMiddle});stack.push(new int[]{leftRow, colMiddle + 1, rowMiddle, rightCol});stack.push(new int[]{rowMiddle + 1, leftCol, rightRow, colMiddle});}else {stack.push(new int[]{leftRow, colMiddle + 1, rowMiddle, rightCol});stack.push(new int[]{rowMiddle + 1, leftCol, rightRow, colMiddle});stack.push(new int[]{rowMiddle + 1, colMiddle + 1, rightRow, rightCol});}}return false;}
}
解法二
思路:
对每行采用二分查找的方法。
代码:
class Solution {public boolean searchMatrix(int[][] matrix, int target) {for (int[] row : matrix) {int index = search(row, target);if (index >= 0) {return true;}}return false;}public int search(int[] nums, int target) {int low = 0, high = nums.length - 1;while (low <= high) {int mid = (high - low) / 2 + low;int num = nums[mid];if (num == target) {return mid;} else if (num > target) {high = mid - 1;} else {low = mid + 1;}}return -1;}
}
解法三
思路:
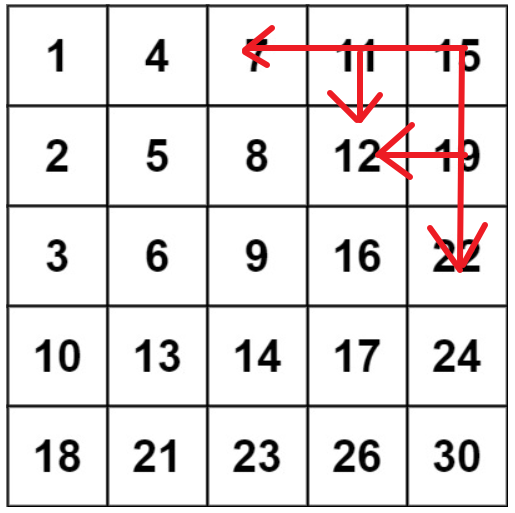
来自官方解答。我们可以从矩阵 matrix 的右上角 (0,n−1) 进行搜索。在每一步的搜索过程中,如果我们位于位置 (x,y),那么我们希望在以 matrix 的左下角为左下角、以 (x,y) 为右上角的矩阵中进行搜索,即行的范围为 [x,m−1],列的范围为 [0,y]:
如果 matrix[x,y]=target,说明搜索完成;
如果 matrix[x,y]>target,由于每一列的元素都是升序排列的,那么在当前的搜索矩阵中,所有位于第 y 列的元素都是严格大于 target 的,因此我们可以将它们全部忽略,即将y减少 1;
如果 matrix[x,y]<target,由于每一行的元素都是升序排列的,那么在当前的搜索矩阵中,所有位于第 x 行的元素都是严格小于 target 的,因此我们可以将它们全部忽略,即将 x 增加 1。
在搜索的过程中,如果我们超出了矩阵的边界,那么说明矩阵中不存在 target。
可以将矩阵类比成一棵二叉排序树,右上角是根节点,旁边就是左右子树。按照排序树的查找方式进行搜查。
代码:
class Solution {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length, n = matrix[0].length;int x = 0, y = n - 1;while (x < m && y >= 0) {if (matrix[x][y] == target) {return true;}if (matrix[x][y] > target) {--y;} else {++x;}}return false;}
}
