I've Got Friends 解题报告
题目大意
有 \(n\) 个人,每个人 \(i\) 有两中喜爱食物 \(f_{i,0},f_{i,1}(f_{i,0}\neq f_{i,1})\)。定义这 \(n\) 个人的友谊集合为 \(S=\{(i,j)|i<j\wedge \{f_{i,0},f_{i,1}\}\cap\{f_{j,0},f_{j,1}\}\neq\varnothing\}\) 。
现在给定 \(n\) 和 \(S\),要求构造一组 \(f_{1,0},f_{1,1},f_{2,0},f_{2,1},\dots,f_{n,0},f_{n,1}\),使得这 \(n\) 个人的友谊集合为给出的 \(S\),或报告无解。
设 \(m = |S|\),则 \(1\leq n\leq 10^5,0\leq m\leq 10^5\),\(S\) 中每个二元组均有 \([1,n]\) 内的两个不同正整数构成,且没有两个相同的二元组。
解题过程
将每个人看作连接 \((f_{i,0},f_{i,1})\) 的边,那么 \(S\) 就是所有有公共端点的边对。即原题转化为求出一个 \(n\) 条边的多重图(即允许重边的图)\(G\),使得其线图 (line graph) 为给定的图 \(H\),\(S\) 即为 \(H\) 的边集。
下面探讨 \(G\) 不存在重边并且连通的情况(连通块之间显然没有影响),最后会说明存在重边的情况只需简单处理。内容参考了 Van Rooij 和 Wilf 发表于 1965 年的论文和 Roussopoulos 发表于 1973 年的论文(见参考资料)。
定理 1:图 \(H\) 是线图,当且仅当存在一系列子图 \(C_1,C_2,\dots,C_k\),其中每个 \(C_i\) 都是完全图,且 \(H\) 中每条边恰好在一个子图中,每个点在不超过两个子图中。称这些子图为一组“划分”,其中每个子图为一个“单元”。
这个定理很容易证明,线图中每个单元就对应了原图中与一个顶点相连的所有边,如果得到了划分那么构造出原图是容易的。这个道理在下面的证明和算法中非常重要,现在算法的目的就变成找到一组划分。
为了便于表述,下面记 \(a\sim b\) 表示点 \(a\) 和点 \(b\) 之间存在边,\(a\nsim b\) 表示 \(a\) 和 \(b\) 之间不存在边。
在关于线图的研究中,有一种重要的结构是”三角形“(三元环),即三个点 \((a,b,c)\) 满足 \(a\sim b,b\sim c, c\sim a\)。同样重要的还有三角形的奇偶性:定义一个三角形 \((a,b,c)\) 是奇的,当且仅当图中存在一个点 \(d\),恰好与 \(a,b,c\) 中 \(1\) 个或 \(3\) 个点相邻;否则这个三角形是偶的。
下面的引理就可以体现三角形和其奇偶性的作用:
引理 1:在线图 \(H\) 的划分中,设边 \((a,b)\) 所在单元为 \(C\),那么所有满足 \((a,b,c)\) 为奇三角形的 \(c\) 都有 \(c\in C\)。
证明考虑反证:假设存在 \(c\notin C\) 使得 \((a,b,c)\) 为奇三角形,那么存在另一点 \(d\) 恰好与 \(a,b,c\) 中的一个或者三个点相邻。
- 若 \(d\) 只与 \(a\) 相邻(\(b\) 同理),那么显然 \(d\notin C\)。又因为 \(d\nsim c\),所以 \((a,d),(a,c)\) 属于两个不同单元且都不是 \(C\),那么 \(a\) 出现在三个单元中,矛盾;
- 若 \(d\) 只与 \(c\) 相邻,那么 \((c,a),(c,b),(c,d)\) 必须属于三个不同单元,矛盾;
- 若 \(d\) 与 \(a,b,c\) 都相邻且 \(d\in C\),那么同上 \((c,a),(c,b),(c,d)\) 属于三个不同单元,矛盾;
- 若 \(d\) 与 \(a,b,c\) 都相邻且 \(d\notin C\),那么 \((a,c),(a,d)\) 必须在同一单元 \(C^{\prime}\) 中。由于 \((a,b)\) 已经在 \(C\) 中所以 \(b\notin C^{\prime}\)。那么 \((b,c),(b,d)\) 必须在两个不同单元中且都不是 \(C\),矛盾。
引理 2:如果图 \(H\) 是线图,那么:
(a) 图 \(H\) 不存在与 \(K_{3,1}\)(即左部 \(3\) 个点、右部 \(1\) 个点的完全二分图,或者说 \(4\) 个点的”菊花图“)同构的子图;
(b) 如果图 \(H\) 中存在两个共边的奇三角形 \((a,b,c),(a,b,d)\),那么 \(c\sim d\),即 \(\{a,b,c,d\}\) 的导出子图为 \(K_4\)。
(a) 的证明较为容易(其实这个思路在引理 1 的证明中已经出现)。假设存在 \(\{a,b,c,d\}\),满足 \(a\sim b,a\sim c, a\sim d,b\nsim c, b\nsim d, c\nsim d\),那么 \((a,b),(a,c),(a,d)\) 三条边中任意两条在划分中显然不能属于同一单元,这就导致点 \(a\) 在至少三个单元中。
(b) 容易由引理 1 得出。
事实上,这两个条件不仅是必要的,也是 \(H\) 是线图的充要条件(证明见参考资料 1)。不过这一点不会在本文中用到。
考虑完共边奇三角形,再来看共边偶三角形:
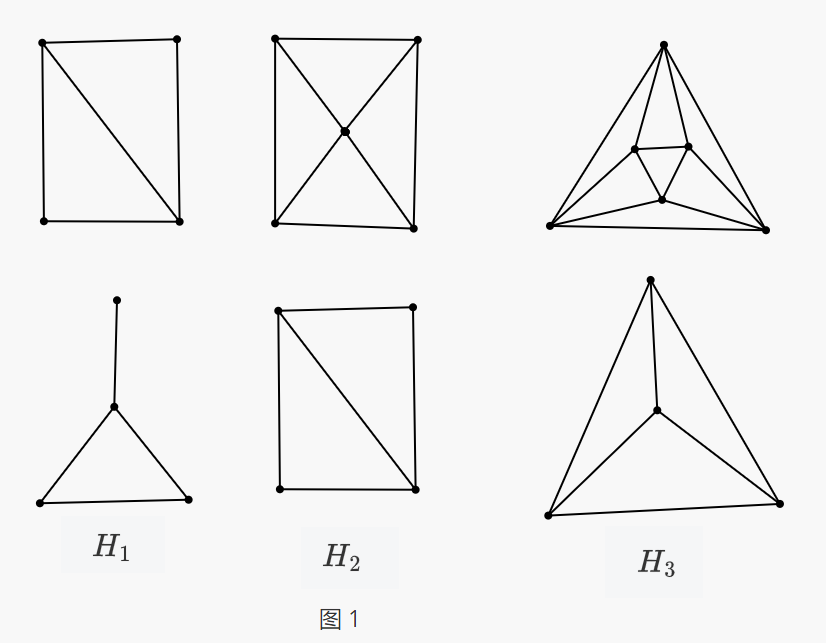
定理 2:如果线图 \(H\) 中有两个共边的偶三角形 \((a,b,c),(a,b,d)\),那么 \(H\) 在同构意义下只有三种可能(记为 \(H_1,H_2,H_3\))。即如果线图 \(H\) 不同构于 \(H_1,H_2,H_3\),那么 \(H\) 中任意两个共边三角形中至少一个是奇的。
容易验证 \(H_1,H_2,H_3\) 是线图(图 1 展示了这三种线图及他们的原图,线图在上,原图在下)
当图中只有 \(a,b,c,d\) 四个点时,对应的线图即为 \(H_1\)。
注意到如果 \(H\) 的任一导出子图不满足引理 2 中的条件,那么 \(H\) 一定也不满足,即 \(H\) 不是线图。
所以可以用程序枚举所有不超过 \(7\) 个点的存在两个共边偶三角形的图,并通过引理 2 来验证,从而证明定理 2.
引理 3:在线图 \(H\) 的划分中,设边 \((a,b)\) 所在单元为 \(C\),包含边 \((a,b)\) 的三角形为 \((a,b,c_1),(a,b,c_2),\dots,(a,b,c_k)\),那么 \(c_1,c_2,\dots,c_k\) 中至少有 \(k-1\) 个在 \(C\) 中。
证明类似引理 1,考虑反证:假设 \(c_1,c_2,\dots, c_l(2\leq l \leq k)\) 均不在 \(C\) 中,那么 \((a,c_1),(a,c_2),\dots,(a,c_l)\) 需要在同一单元 \(C_a\) 中,\((b,c_1),(b,c_2),\dots,(b,c_l)\) 需要在同一单元 \(C_b\) 中。由于 \((a,b)\) 在 \(C\) 中,所以 \(C_a\neq C_b\) 。但此时 \(C_a,C_b\) 都包含了边 \((c_1,c_2)\),矛盾。
引理 4:如果图 \(H\) 有同构于 \(K_r(r\geq 4)\) 的导出子图,那么其中每个三角形都是奇的。
正确性显然。
下面的定理为本文的算法提供了重要的思路和理论支撑:
定理 3:设线图 \(H\)(不是 \(H_1,H_2,H_3\))中边 \((a,b)\) 共在 \(k(k\geq 2)\) 个三角形中,其中有 \(l\) 个奇三角形 \((a,b,c_1),(a,b,c_2),\dots,(a,b,c_l)\),那么有:
(a) \(l=k-1\) 或 \(l=k\);
(b) \(\{a,b,c_1,c_2,\dots,c_l\}\) 的导出子图一定是 \(H\) 的划分中的一个单元。
(a) 由定理 2 容易证明。
(b) 是引理 1 的扩展,由引理 1 知 \(a,b,c_1,c_2,\dots,c_l\) 一定在同一个单元中。由引理 4 知如果 \(l=k-1\),那么 \(\{a,b,c_1,c_2,\dots,c_k\}\) 的导出子图不可能是完全图,否则 \((a,b,c_k)\) 应为奇三角形。而任何 \(x\notin\{a,b,c_1,c_2,\dots,c_k\}\) 不能同时和 \(a,b\) 有边,故也不在这个单元中。
下面描述了判断 \(H\) 是否是线图并构造原图的算法,其中步骤 1,2 找到了一个单元,步骤 3 从这个单元开始构造了一个划分,步骤 4 通过划分构造原图 \(G\):
- 任取 \(H\) 中一条边 \((a,b)\) 统计其所在的三角形数量,设为 \(k\):
- 若 \(k=0\),则 \((a,b)\) 一定为一个同构与 \(K_2\) 的单元,转到步骤 3;
- 若 \(k=1\),设该三角形为 \((a,b,c)\)。统计 \((a,c),(b,c)\) 所在三角形数量若均为 \(1\),则容易说明此时 \(H\) 如果不是 \(K_3\),则 \(\{a,b,c\}\) 的导出子图一定一个单元,转到步骤 3。若 \((a,c)\) 在不小于 \(2\) 个三角形中,则用 \((a,c)\) 代替 \((a,b)\) 转到步骤 2,\((b,c)\) 同理;
- 若 \(k\geq 2\),转到步骤 2。
- 统计 \(k\) 个三角形中奇三角形个数,设为 \(l\),那么:
- 如果 \(k = 2,l=0\),此时 \(H\) 可能为 \(H_1,H_2,H_3\) 或者不是线图,将其中任意三角形作为起始单元转到步骤 3(容易验证对于这三种图这样都能正确构造);
- 否则如果 \(l<k-1\),由定理 3,\(H\) 不为线图;
- 如果 \(l=k\) 或 \(l=k-1\),那么由定理 3 也找到了一个单元,判断这个导出子图是否是完全图,转到步骤 3。
- 现在已经找到了划分中的一个单元 \(C_1\),那么由于每个点至多在两个单元中,所以 \(C_1\) 中每个点 \(x\) 如果有不在 \(C_1\) 中的边 \((x,y_1),(x,y_2),\dots,(x,y_s)\),那么 \(\{x,y_1,y_2,\dots,y_s\}\) 的导出子图一定是下一个单元。一直这样递归下去,如果出现导出子图不是完全图或一个点出现在三个单元中,则 \(H\) 不是线图。否则由 \(H\) 连通,必然会将得到一个合法的构造。
- 得到划分后,为每个单元在 \(G\) 建一个点,并作为单元中每个点在 \(G\) 中对应的边的一个端点。如果一个 \(H\) 中的点只在一个划分中,则将 \(G\) 中对应边的另一个端点设为一个仅与这条边相邻的新点。
步骤 1,2 精细实现可以做到 \(O(n+m)\) 的复杂度。步骤 3 中每个点只会访问不超过 \(3\) 次,故复杂度也可以做到 \(O(n+m)\)。步骤 4 容易做到 \(O(n+m)\)。
至此得到了一个 \(O(n+m)\) 复杂度的构造线图对应的原图的算法。
最后,对于 \(G\) 可能存在重边的情况,设 \(A_i\) 为 \(i\) 在 \(H\) 中所有相邻点和 \(i\) 自己构成的集合,那么将所有 \(A_i\) 相同的 \(i\) 构造为重边,并对于每种 \(A_i\) 只保留这些 \(i\) 中的一个,不难发现这样处理不改变答案的存在性。借助哈希容易以 \(O(n+m)\) 的复杂度完成。
总复杂度 \(O(n+m)\)。
参考资料
- van Rooij, A. C. M., & Wilf, H. S. 1965. "The interchange graph of a finite graph". Acta Mathematica, 16(3-4), 263–268.
- Roussopoulos, Nicholas D. 1973. "A max {m,n} Algorithm for Determining the Graph H from Its Line Graph G." Information Processing Letters 2 (4): 108-112.
