齐次坐标
介绍仿射变换前,先介绍什么是齐次坐标。对于一个平面像素点,我们可以通过坐标(x,y)描述其位置。但是当涉及平移时,如果仅仅使用它对应的坐标向量[x,y],就必须通过向量加法来描述其位移。 而齐次坐标的引入就是为了统一在变化过程中的操作,我们希望能够通过一个 Pt=TP0,这样一个乘法公式去统一描述对像素点的平移和旋转操作。

齐次坐标是一种用N+1维向量表示N维空间点的方法。在二维空间下,其标准形式为[x,y,1]。对于一个点,我们直接在最后补上一个1,就转换成了齐次坐标。
引入其次坐标后,该平移操作可以表示为

旋转
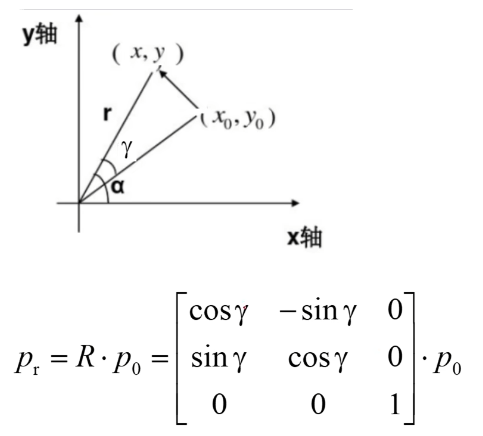
此处,简要介绍在齐次坐标下如何描述旋转操作。公式可以自己推导以下,利用已知角的三角函数和坐标值计算旋转后的点坐标。
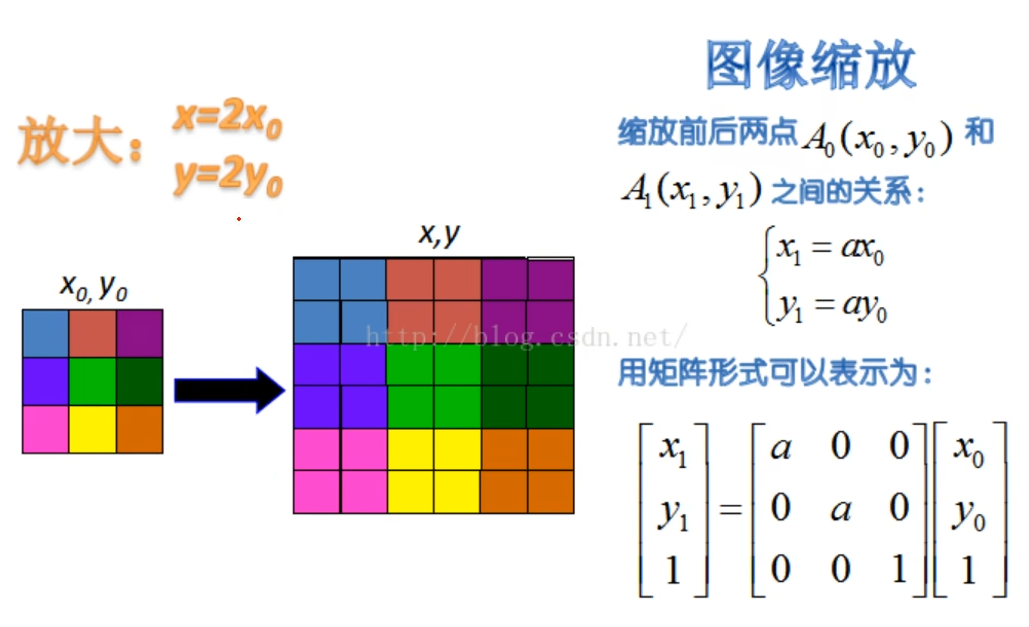
缩放
当放大时a>1,当缩小时0<a<1。放大后的图像,就相当于把原来的点扩大了多份。
几何变换

相似变换

相似变换中,缩放必须为等比例的缩放。
仿射变换

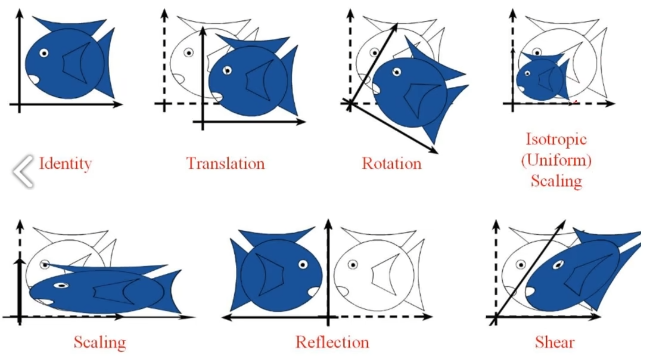
仿射变换只保证直线不发生弯曲以及平行线变换后仍然是平行线,因此物体可能会发生形变(变换后两条直线夹角不同)。

下面是几种仿射变换的类型。Identity对应的就是不发生任何变换,在Halcon我们也是使用hom_mat2d_identity,算子去创建一个空的2D变换齐次矩阵的。
切变
图像向某一方向倾斜。

镜像
实际上就是旋转

投影变换

Halcon中使用仿射变换
其他参数很好理解,对于最后一个参数就是是否自适应调整图像的大小,防止变换后的图像显示不全等。

