- 单层感知机的局限性
• 单层感知机能做的只是用 一条直线 / 超平面 来分隔数据。
• 问题:遇到 异或(XOR)问题 或者更复杂的数据分布,就没办法仅靠一条直线来分开。
例如:
• 点 (0,0) 和 (1,1) 属于一类
• 点 (0,1) 和 (1,0) 属于另一类
👉 这两个类别在二维平面上是“交叉”的,用一条直线永远分不开。
⸻
- 多个线性方程组合的想法
虽然一条直线不够,但我们可以 多画几条直线,把空间划分成多个区域,再用这些区域的交集/并集来表示复杂分类边界。
数学上:
• 每一个感知机相当于一个线性方程(超平面)。
• 多个感知机组合起来,就可以圈定复杂形状的区域。
⸻
- 直观例子:用两个感知机圈定区域
设二维空间:
• 感知机 1:\(x_1 + x_2 - 1 \ge 0\) (一条直线)
• 感知机 2:\(x_1 - x_2 \ge 0\) (另一条直线)
这两条直线交叉后,会把平面划分成四个区域。
我们可以用 逻辑组合(例如“同时满足”)来圈定某个区域,从而表示异或等复杂分类。
⸻
- 代码实验:XOR 问题
我们用两个感知机组合,尝试分类 XOR 数据:
import numpy as np
import matplotlib.pyplot as plt# XOR 数据集
X = np.array([[0,0],[0,1],[1,0],[1,1]])
y = np.array([0,1,1,0]) # 异或输出# 定义两个线性函数(人为设定,不训练)
def h1(x): return 1 if x[0] + x[1] - 0.5 >= 0 else 0
def h2(x): return 1 if x[0] - x[1] >= 0 else 0# 组合:异或近似 = h1(x) XOR h2(x)
def xor_like(x):return h1(x) ^ h2(x)# 可视化
colors = ['red' if label == 1 else 'blue' for label in y]
plt.scatter(X[:,0], X[:,1], c=colors, s=100, edgecolors='k')# 画出直线
xx = np.linspace(-0.5, 1.5, 100)
plt.plot(xx, -xx+0.5, 'g--', label='h1: x1+x2=0.5')
plt.plot(xx, xx, 'm--', label='h2: x1=x2')plt.legend()
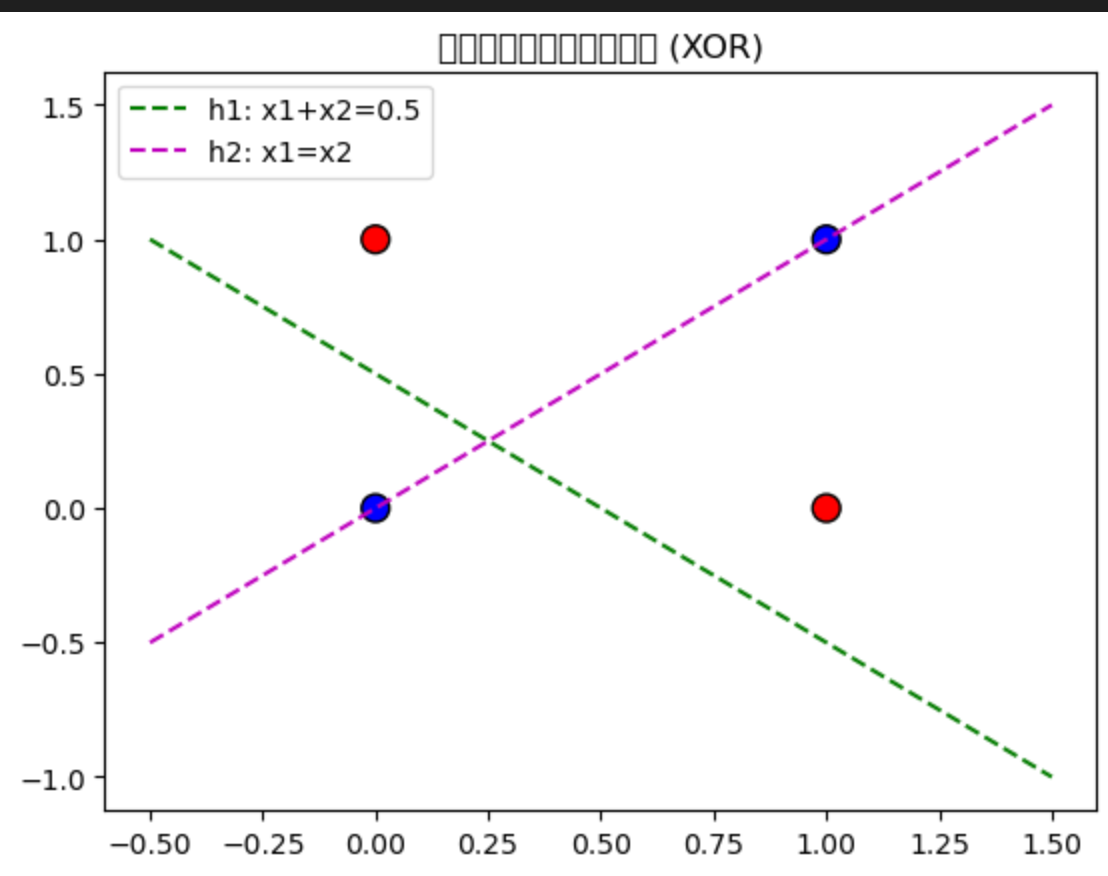
plt.title("多个感知机组合圈定区域 (XOR)")
plt.show()# 测试输出
for xi in X:print(xi, "->", xor_like(xi))
5:
