《电路基础》第六章学习笔记
本章我们将学习电容和电感电路。
-
电容器
-
构成:
电容器由被绝缘体(电介质)隔开的两个导电金属极板组成
-
高中知识:
\[q=Cv \]\[C= \frac{\varepsilon A}{d} \]其中A为各个极板的表面积,d为两极板之间的距离。\(\varepsilon\) 为介电常数。
-
常见的可变电容器

为了得到电容器的电流——电压关系,我们通过微分得到:
\[i=C\frac{\mathrm{d}v}{\mathrm{d}t } \]两边取微分,得到:
\[v=\frac{1}{C}\int_{t_{0}}^{t} i\mathrm{d}t+v(t_{0}) \] -
电容器的性质:
-
对直流电而言是开路的
-
电压不能突变,必须是连续的
-
理想电容器不消耗能量
-
实际的非理想电容器包括一个并联的泄露电阻,阻值高达100MΩ,对绝大多数实际应用而言是可以忽略不计的。
-
-
电容器的串联与并联
我们可以用一个等效电容 \(C_{eq}\) 取代若干个电容的串联或并联。
-
N个并联连接的电容器的等效电容等于各电容器的电容之和
证明过程:
\[i=(\sum_{k=1}^{N}C_{k})\frac{\mathrm{d}v}{{d}t}=C_{eq}\frac{\mathrm{d}v}{{d}t} \]所以:
\[C_{eq}=C_{1}+C_{2}+C_{3}+\dots+C_{N} \]
-
串联电容器的等效电容等于各个电容器电容倒数之和的倒数
(咦,这不就是鸡在河上飞哈哈哈哈)
总结:电容的串并联刚好与电阻相反。
\[C_{eq}=\frac{C_{1}C_{2}}{C_{1}+C_{2}} \]
-
-
-
电感
-
构成:
电感器由导线线圈组成
-
定义:
\[v=L\frac{\mathrm{d}i}{\mathrm{d}t} \]其中L为比例常数,称为电感,单位是亨利(H)
电感反映的是电感器阻碍流经它的电流变化的属性
-
电感器两端要有电压,其电流必须随时间而变化。
对于螺线管线圈电感器,其电感量为:
\[L=\frac{N^2\mu A}{\ell} \]其中N为线圈匝数,\(\ell\) 为螺线管的长度,A为横截面积,\(\mu\) 为磁芯的导磁率。
-
不同类别的电感和电路符号

-
电流表达式
\[i=\frac{1}{L}\int_{t_{0}}^{t}v(t) \mathrm{d}t +i{t_{0}} \]存储的能量为:
\[w=\frac{1}{2}Li^2 \] -
特性:
-
电感器对直流电而言是短路的(电容是开路)
-
流经电感器的电流是不能突变的。
- 电感器两端的电压是可以突变的
-
理想电感也不消耗能量
-
实际的非理想电感包含一个非常重要的电阻,与电感串联,还存在一个匝间绕线电容。除高频情况外,\(C_{q}\) 通常很小,在大多数情况下可以忽略不计。

-
-
-
积分器
-
定义:
积分器是一种输出信号与输入信号的积分呈正比的运放电路。

在施加输入信号之前,必须先对积分器的电容器放电,使 \(v_{o}\)(0)=0 ,则有:
\[v_{o}=-\frac{1}{RC} \int_{0}^{t} v_{i}(t)\mathrm{d}t \]
-
-
微分器
-
定义:
一种输出信号与输入信号的变化率呈正比的运放电路。
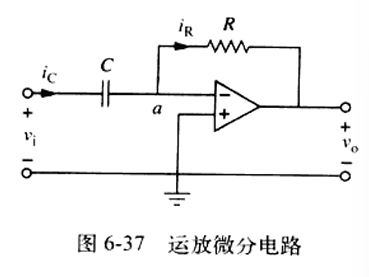
如图,应用KCL可以得到:
\[v_{o}=-RC\frac{\mathrm{d}v_{i} }{\mathrm{d}t } \]
-
