数论分块用于求解形如 \(\sum_{i=1}^n\lfloor\frac ni\rfloor\) 的含有向下取整的求和式子,是可以将原本 \(\mathcal O(n)\) 复杂度优化至 \(\mathcal{O}(\sqrt n)\) 的超强实用算法,常与莫比乌斯反演配套使用,同时也是学习莫反的前置芝士
鉴于数论分块非常优秀的时间复杂度,当你看到出题人将数据范围给到 \(n\leq 10^{12}\) 这种连 \(\mathcal{O}(n)\) 都过不了的逆天大小时,请务必考虑数论分块!
这篇只会讨论一般的整除分块,至于各种拓展就先放着以后再说好了
数论分块的思想主要在于将 \(\lfloor\frac ni\rfloor\) 的值相同的项同时计算,一段区间内的数只需要算一次即可,用一个图形象展示一下数论分块:
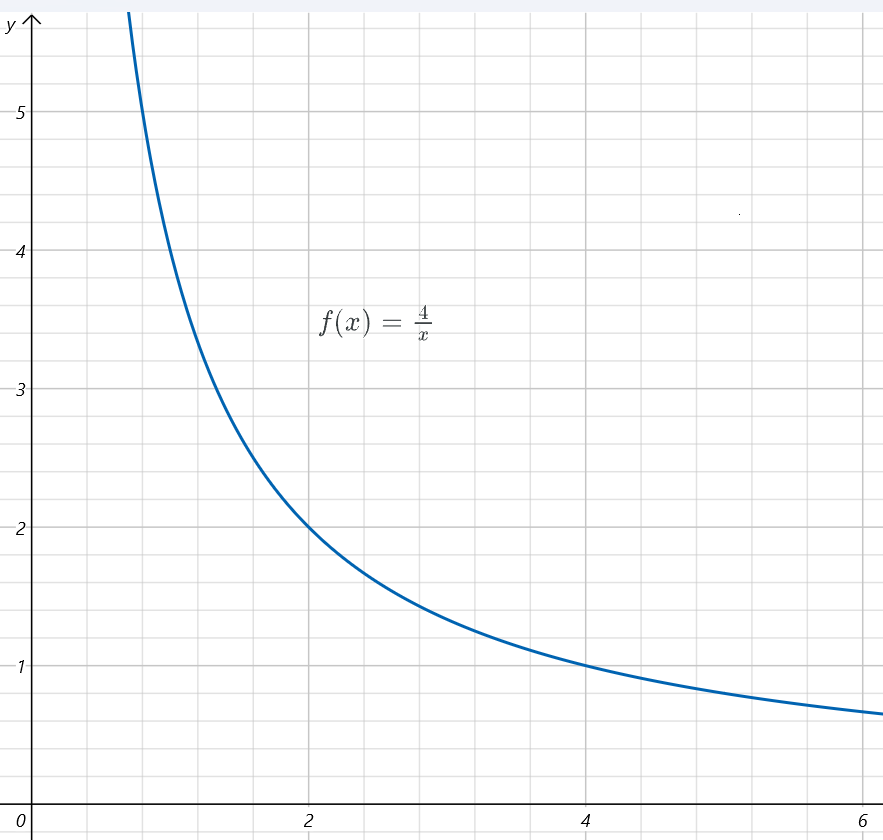
这是一段反比例函数 \(f(x)=\frac4x\) 的图像,如果将这个函数改变一下变成 \(f(x)=\lfloor\frac4x\rfloor\),上面的函数就会被分成几块,如下图:
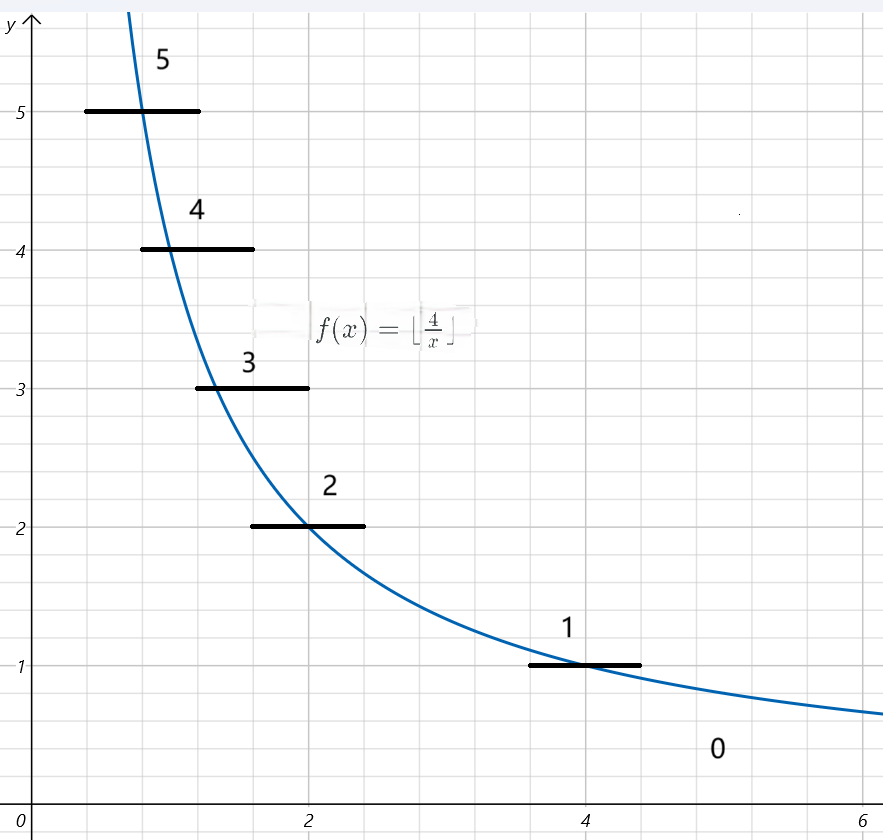
黑线把蓝线函数划分成不同的线段,每一块都有对应的一个确定的数值,分块大抵就是这样分的图很烂凑合着看看
如此,只要能确定每一个块的区间 \([l,r]\) 就可以快捷计算了。
先说结论:对于一个分块 \(\lfloor\frac ni\rfloor\),\(\lfloor\frac ni\rfloor\) 的值相等的区间的两端为 \([i,\lfloor\frac{n}{\lfloor\frac ni\rfloor}\rfloor]\)
左端点为\(i\)应该很好理解,重点证明右端点。
没什么必要的引理:
无需证明。
证明过程:
要证明\(\lfloor\frac{n}{\lfloor\frac ni\rfloor}\rfloor\)为区间右端点,要证明两个式子:
首先证明\(\lfloor\frac{n}{\lfloor\frac ni\rfloor}\rfloor\)和\(i\)在同一个块中,即:$$ \lfloor\frac{n}{\lfloor\frac{n}{\lfloor\frac ni\rfloor}\rfloor}\rfloor=\lfloor\frac ni\rfloor $$由于:$$\lfloor\frac{n}{\lfloor\frac{n}{\lfloor\frac ni\rfloor}\rfloor}\rfloor \geq \lfloor\frac{n}{\frac{n}{\lfloor\frac ni\rfloor}}\rfloor = \lfloor{\lfloor\frac ni\rfloor}\rfloor = \lfloor\frac ni\rfloor$$
且:$$\lfloor\frac{n}{\lfloor\frac{n}{\lfloor\frac ni\rfloor}\rfloor}\rfloor \leq \lfloor\frac{n}{\lfloor\frac{n}{\frac ni}\rfloor}\rfloor = \lfloor{\frac n{\lfloor i\rfloor}}\rfloor = \lfloor\frac ni\rfloor$$
则有:$$\lfloor\frac{n}{\lfloor\frac{n}{\lfloor\frac ni\rfloor}\rfloor}\rfloor=\lfloor\frac ni\rfloor$$
得证
其次证明 \(\lfloor\frac n{\lfloor\frac ni\rfloor}\rfloor\) 是这个块的最大取值,即:$$\lfloor\frac n{\lfloor\frac ni\rfloor}\rfloor \geq i$$$$\lfloor\frac n{\lfloor\frac ni\rfloor}\rfloor \geq \lfloor\frac n{\frac ni}\rfloor = \lfloor i\rfloor=i$$
得证
于是要求 \(\sum_{i=1}^n\lfloor\frac ni\rfloor\) 就可以每次以 \([l,r]=[l,\lfloor\frac n{\lfloor\frac nl\rfloor}\rfloor]\) 为一个块计算如下:
注意:如果偶遇形如 \(\sum_{i=1}^nf(i)g(\lfloor\frac ni\rfloor)\) 这种混了其他东西的求和,则需要预处理出 \(f(i)\) 的前缀和,才能按照 \(\mathcal{O}(\sqrt n)\) 计算求和,设 \(s(i)=\sum_{j=1}^if(j)\),则计算过程如下:
注:按照OI WIKI的说法,若能在 \(\mathcal{O}(1)\) 内求出 \(f(r)-f(l)\) 的值,也可以按照 \(\mathcal O(\sqrt n)\) 的时间计算数论分块但是我还没搞懂这是啥意思。
总之核心代码很短,如下:
ans = 0;
for (int l = 1,r = 0;l <= n;l = r + 1)
{r = n / (n / l);ans += (r - l + 1)*(n / l);
}
模板题UVA11526 H(n)直接按上面模板就行了。
