势能分析太厉害了!
势能分析主要是计算一些过程十分复杂的算法的时间复杂度。我们巧妙地借助物理中的势能解决问题,我们先定义一个状态的势能,将复杂度刻画为引起势能变化所做的功,而关于势能很多时候我们只关心始末状态,无序关心中间的具体做功情况,恰好能解决中间流程复杂的问题。
并且,势能分析主要用于分析一些均摊复杂度问题。我们可以把势能理解为“预付代价”,将过程前后联系起来。
具体的,我们将进行 \(n\) 次操作,定义 \(c_i\) 表示第 \(i\) 次操作所花费的时间,\(F(S)\) 表示状态 \(S\) 的势能,第 \(i\) 次操作结束时的状态为 \(S_i\),我们将第 \(i\) 次操作的摊还复杂度 \(\hat{c}_i\) 定义为:
于是,\(n\) 次操作的摊还复杂度即为:
而我们要求的是 \(\sum_{i=1}^n c_i\),我们可以通过计算 \(T\) 和 \(F(S_n)-F(S_0)\) 的下界算出真实复杂度的上界。
刚开始学的人可能会有一些误区,做功显然不是只做正功,也有可能做负功。且我们主要是利用势能很好的性质,将操作与势能联系起来,通过若干数学技巧算出摊还复杂度,总之就是摊还复杂度和真实复杂度是不一样的,摊还复杂度还囊括了势能的影响。
对于一些很简单的问题我就不多讲了,我采取欧美打法,直接讲 Splay 和 LCT 复杂度的证明。
Splay 复杂度证明
我们定义 \(|x|\) 为 \(x\) 的子树大小,对每个点构造势能函数 \(\phi(x)=\log|x|\),Splay \(S\) 的势能函数为 \(\phi(S)=\sum_{x\in S}\phi(x)\)。
很明显我们只需要证明 splay 函数的复杂度是对的即可,其它操作只会增加常数。我们不难求出 \(\phi(S_n)-\phi(S_0)\) 的下界为 \(-n\log n\),接下来考虑计算摊还复杂度。
对于一次 rotate,我们花费的摊还复杂度显然是 \(\mathcal{O}(1)+\phi(x')-\phi(x)\)。
对于 splay 的双旋,一字型旋转和之字形旋转,我贺了洛谷日报的图:
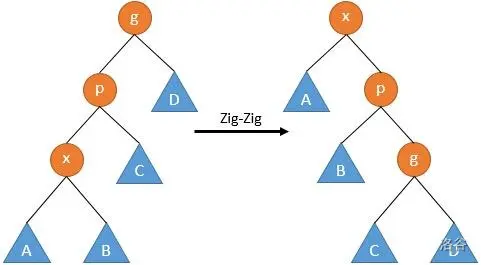
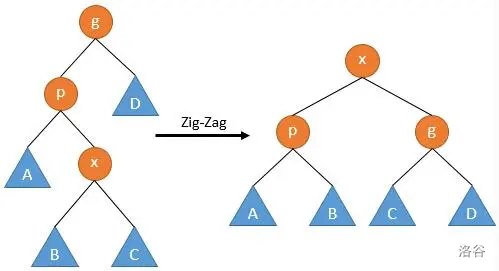
先考虑前者。我们的 \(\hat c_i=\mathcal{O}(1)+\Delta \phi(S)\),\(\Delta\phi (S)\) 的计算我们考虑用操作涉及涉及到的六个点刻画,我们不妨令操作 \(x,p,g\) 完之后代表的点变成 \(x',p',g'\)。那么
注意到 \(\phi(x')=\phi(g)\),\(\phi(g')<\phi(x')\),\(\phi(p)>\phi(x)\),于是有
我们尝试将 \(\phi(p')\) 消掉,考察 \(\phi(x)+\phi(p')-2\phi(x')\) 的性质。写出原式
注意到 \(|x'|>|x|+|p'|\),于是不难放缩出
直接整体做减法可得
于是
其中后面的 \(\mathcal{O}(1)\) 被 \(-1\) 均摊掉了。
对于后者,我们采取类似的分析,\(\Delta\phi(S)=\phi(p')+\phi(g')-\phi(p)-\phi(x)<\phi(p')+\phi(g')-2\phi(x)\),考察 \(\phi(p')+\phi(g')-2\phi(x')\),发现仍然有小于 \(-1\),直接做减法然后算出
我们知道,一次 splay 顶多一次单旋,于是一次操作摊还复杂度可以视作 \(\mathcal{O}(\log n)+\mathcal{O}(1)=\mathcal{O}(\log n)\)。
看完了证明,我们将解决很多对于 splay 的一些一直不知道原因的问题:
- 为什么一字型旋转必须先旋父亲?因为不先旋父亲找不到类似 \(a+b<c,\log(\frac {a+b}{c^2})<-1\) 的性质,事实上它根本减少不了深度,我们一直加点就能卡掉。
- 为什么操作到哪就得 splay 到哪?这是个好问题。肤浅的人会认为 splay 保证了树高,这并没错,但是这不代表每一时刻都能控制在 \(\mathcal{O}(\log n)\) 内。注意了,我们复杂度证明算的可是摊还复杂度,跟实际复杂度已经是两码事了,总之,splay 是依赖于均摊的复杂算法,并不能肤浅地认为树高保持在 \(\mathcal{O}(\log n)\) 内,如果操作不 splay,我们相当于是独立于摊还证明之外了。
- 为什么不上手法的 treap 不能用在 LCT 中?这个待会讲 LCT 时再讲。
LCT 复杂度证明
类似的,LCT 时间复杂度本质上之来自于 access 操作。
这个我们分成两部分证明,一部分是 splay 的复杂度,一部分是在树上跳虚边的复杂度。
这边我只证明它的摊还复杂度,证完摊还再证实际复杂度是容易的。
Splay 中
我们定义 \(|x|\) 为 \(x\) 在当前树中的子树大小,当前树定义为由所有虚边和 splay 的边组成的树。不妨还是令 \(\phi(x)=\log |x|\),状态 \(S\) 的势能 \(\phi(S)=\sum_{x\in S}\phi(x)\)。
一次 access 操作中,不妨设它在树上跳虚边的时候一次访问了 \(x_1,x_2,\cdots,x_k\),而在之间的一棵 splay 中我们带来的摊还复杂度为 \(\mathcal{O}(1)+\Delta\phi(S)< \phi(x_i)-\phi(x_{i-1})\),小于的原因是 \(x_i\) 显然是 \(x_{i-1}\) 的 splay 上的根的父亲。于是加起来的摊还复杂度仍然能抵消,并满足 \(\mathcal{O}(\log n)\)。
最后实际复杂度就是摊还加上变化上界,即 \(\mathcal{O}((n+m)\log n)\)。
虚边上
考虑结合重链剖分进行分析。定义重虚边为既是重边又是虚边的数量,那么定义势能函数 \(\Phi\) 为所有重虚边的数量。
那么,我们每次最多走 \(\log\) 条轻虚边,也就是说至多带来 \(\log\) 条重虚边,均摊的很优雅。
而对于重虚边转轻虚边需要花费 \(\mathcal{O}(1)\) 的代价减小 \(1\) 的势能,对于做功常量,也就是轻虚边之间我们不用考虑,因为重链剖分的经典结论保证最多经过 \(\mathcal{O}(\log n)\) 条轻边。
于是复杂度直接就对了,因为我们总共最多就 \(\mathcal{O}(n+m\log n)\) 条轻虚边。
综上所述,LCT 复杂度为 \(\mathcal{O}((n+m)\log n)\)。
通过我们的过程同样可以说明,LCT 也必须要操作到哪 access 到哪,并且,发现我们的过程利用了 splay 的摊还复杂度,而对于不上手法的 treap,复杂度可能会退化到两只老哥。
对于并查集的一些复杂度我先鸽了,有时间再写。
