题目传送门
当时这个题是我考试题,考试的时候感性理解出来的三分做法。
首先咱感性理解一下,当\(x_0\)位于左边无穷远处时,答案是个很大的数。
然后随着\(x_0\)从左向右移动,答案呈递减趋势。当\(x_0\)到达答案那个点时,距离最小。然后\(x_0\)接着向右移动,答案又递增。当\(x0\)位于右侧无穷远处时,答案又会趋近于无穷大。
所以我们猜想,\(ans\)随\(x_0\)变化的函数先递减再递增。当\(x_0\)位于谷底时,\(ans\)就会取最小值。
接下来我们简单证明一下结论。
首先我们设\(i\)到集合地点所需时间关于\(x_0\)的函数为\(f(x_0)\)。显然\(f(x_0)=|x_0-x_i|+t_i\),图像如下:
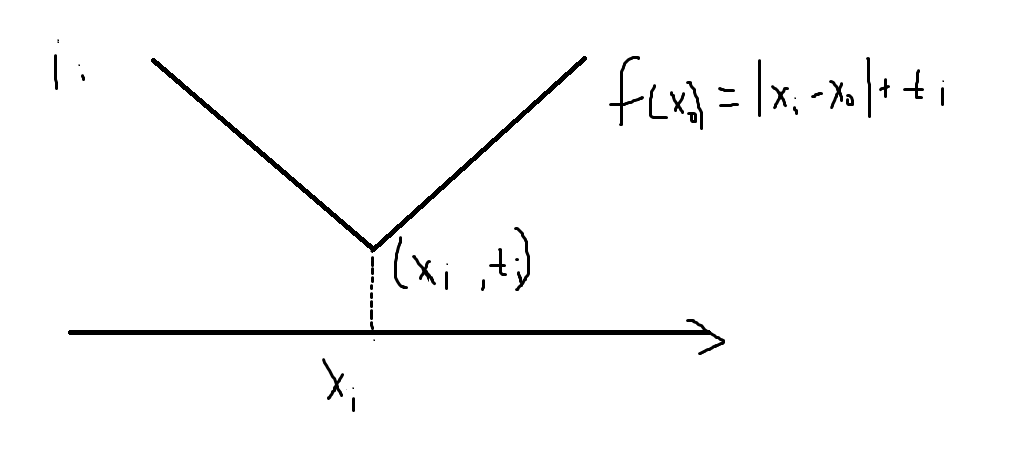
这是一个折线。对于其他的\(i\),也应该是这样的折线。我们把所有的\(n\)条折线画在同一平面直角坐标系中,大概这样:

而对于一个确定的\(x_0\),聚集时间就是这一坨函数里\(x_0\)对应的因变量的最大值,对应到图像里就是\(x=x_0\)与各个图像交点里最高的点的纵坐标。
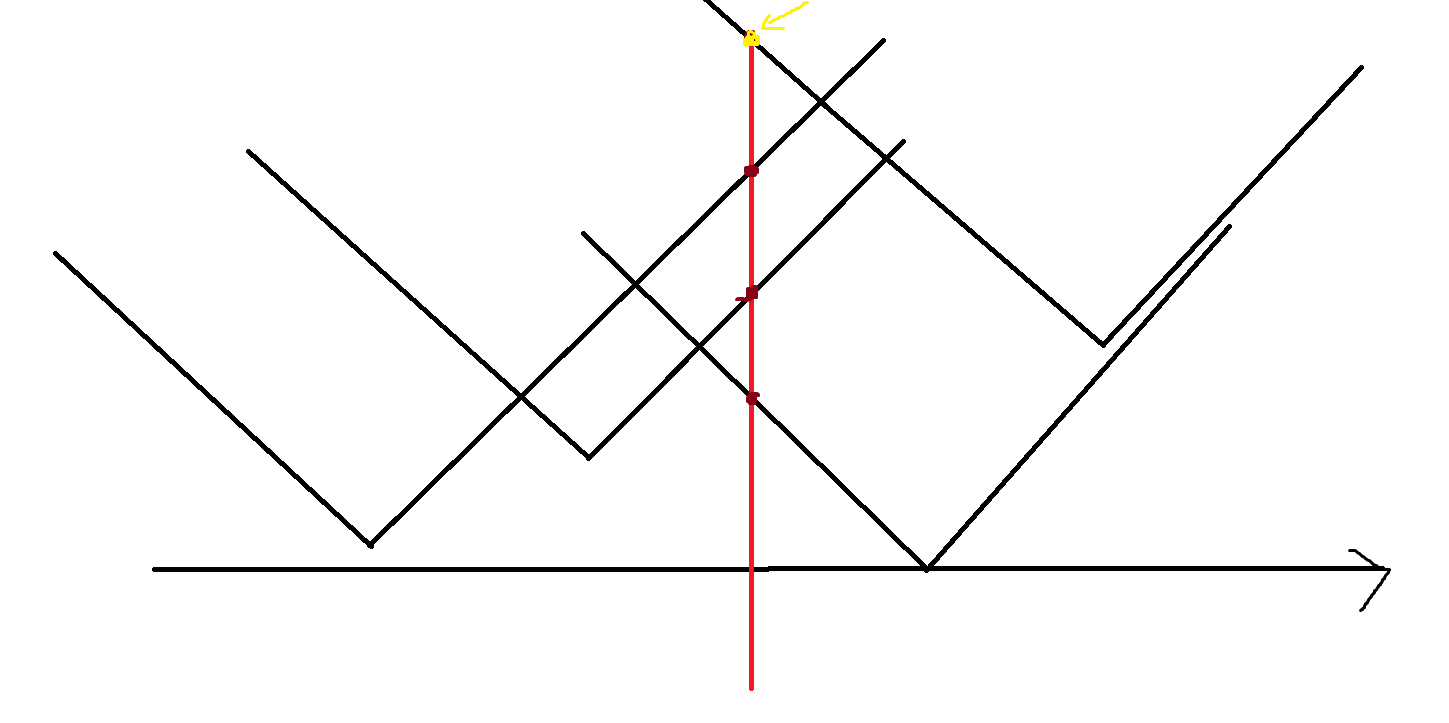
至于聚会时间关于\(x_0\)的函数图像,很明显就是对于每个横坐标\(x_0\)都取一下最大值得到的点组成的图像。比如这样。
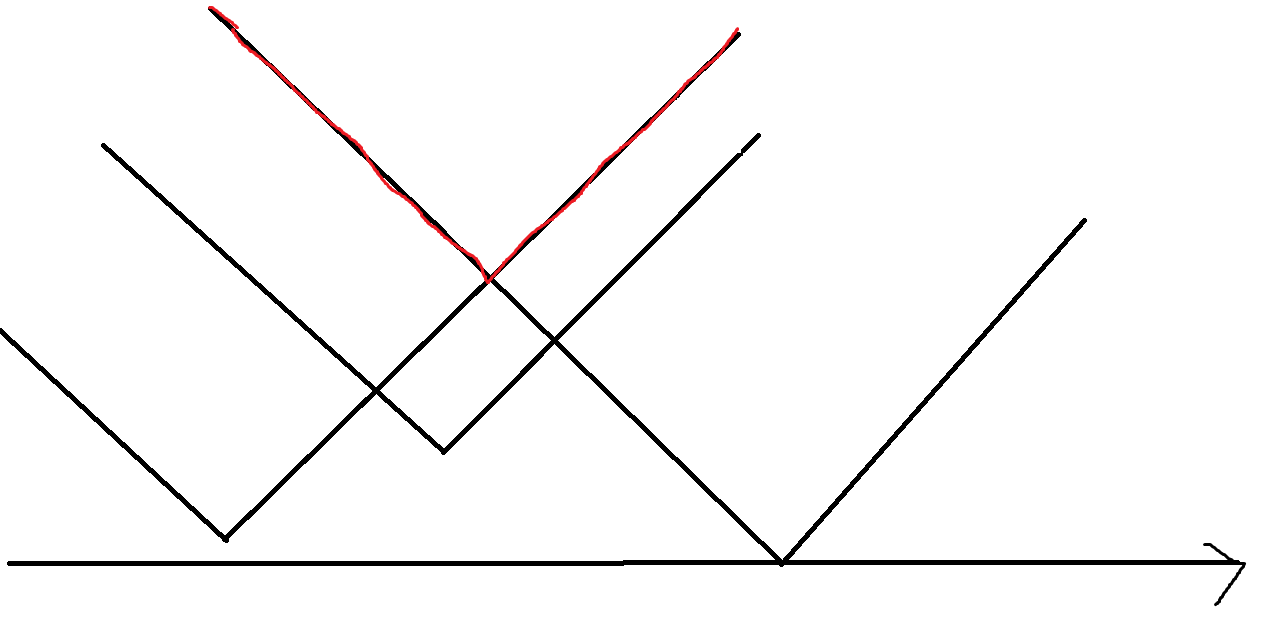
看起来,对于这种情况来说是个折线。但是如何说明其他情况也是折线呢?
我们把这个过程看作一个函数图像两两合并的过程,也就是对于两个函数做上面的过程。这样事情就会简单很多,因为它们的斜率相同,位置关系无非是包含和相交两种。
如果是包含的话,显然合并后结果就是上面的函数。这种情况下两根折线合并后还是折线。

如果是相交的话,各取两个函数比较高的线,最终还是个折线。

所以折线间两两合并,最终结果还是折线,也就证明了我们可以用三分解决本题。
代码:
P11854
#include<bits/stdc++.h>
#define int long long
using namespace std;inline int read(){int x=0,f=1;char c=getchar();while(c<48){if(c=='-') f=-1;c=getchar();} while(c>47) x=(x<<1)+(x<<3)+(c^48),c=getchar();return x*f;
}const int N=1e5+5;
const int inf=1e16;
const double sta=1e-5;
const double STA=0.01;
int T,n,pos[N],t[N];inline double f(double x){double ans=0;for(int i=1;i<=n;i++){ans=max(ans,fabs(pos[i]-x)+t[i]);}return ans;
}signed main(){T=read();while(T--){n=read();int mi=inf,ma=0;for(int i=1;i<=n;i++){pos[i]=read();mi=min(mi,pos[i]);ma=max(ma,pos[i]);}for(int i=1;i<=n;i++){t[i]=read();}//实数三分 double l=mi,r=ma;//显然答案不会在这个区间外 while(r-l>sta){double lmid=l+(r-l)/3,rmid=r-(r-l)/3;double ans1=f(lmid),ans2=f(rmid);//f(x0):求聚会时间 if(ans1>ans2){l=lmid;}else{r=rmid;}}//底下是自制的一个判断整数//具体来说,如果最终结果与它相邻的两个整数的误差不超过允许的范围,那我们就认为它是整数,否则就是小数 double ll=floor(l);double lll=ceil(l);if(STA>l-ll){int ans=ll;printf("%lld\n",ans);}else if(STA>lll-l){int ans=lll;printf("%lld\n",ans);}else{printf("%.1lf\n",l);}}return 0;
}
