题意:平面上有 \(n\) 个点 \((i,p_i)\),\(p\) 是一个排列。每次操作可以选择 \(x/y\) 和一个坐标,将点列分成左右/上下两边(保持两边的相对顺序不变),分别递归下去,直到只剩下一个点,把它加入答案序列末尾。求最终能生成多少种不同的答案序列。
做法:
首先很自然地考虑目前剩下的矩形为 \(x\in[l,r],y\in[u,d]\),记此时的答案为 \(f_{l,r,u, d}\)。考虑一刀劈成两半继续递归,但是显然这样直接算是错的,考虑如下情况:
- 只有 \((1,1),(2,2)\) 两个点。
此时你做对 \(x\) 轴和 \(y\) 轴的操作是没有区别的。
那么对于这种会重复的我们一般考虑加一些限制使他不会重复。这里我们先定义一些东西,考虑现在这个区域中剩下了 \(k+1\) 个点,离散后应该会剩下 \(x_1<x_2<\cdots <x_k\),\(y_1<y2<\cdots <y_k\) 这些 切割线是有用的。我们考虑这么定义一个操作的字典序,按字典序从小到大排是 \(x_1,y_1,x_2,y_2,\cdots,x_k,y_k\)。这样排有什么好处呢?按字典序我们就可以让一种答案序列对应唯一一种操作序列,同时交错排布会有利于我们之后的分讨。
考虑如果一个操作序列第一刀切在的 \(x_i\) 这个位置,我们先算出来切在这里的总方案数,为 \(f_{l,x_i,u,d}\times f_{x_i+1, r,u,d}\)。但是有可能有操作序列字典序更小的得到了这个答案序列,考虑是 \(x_j\) 还是 \(y_j\)。
- 由 \(x_j(j<i)\) 得到。
画图,那么应该分为这么几块:
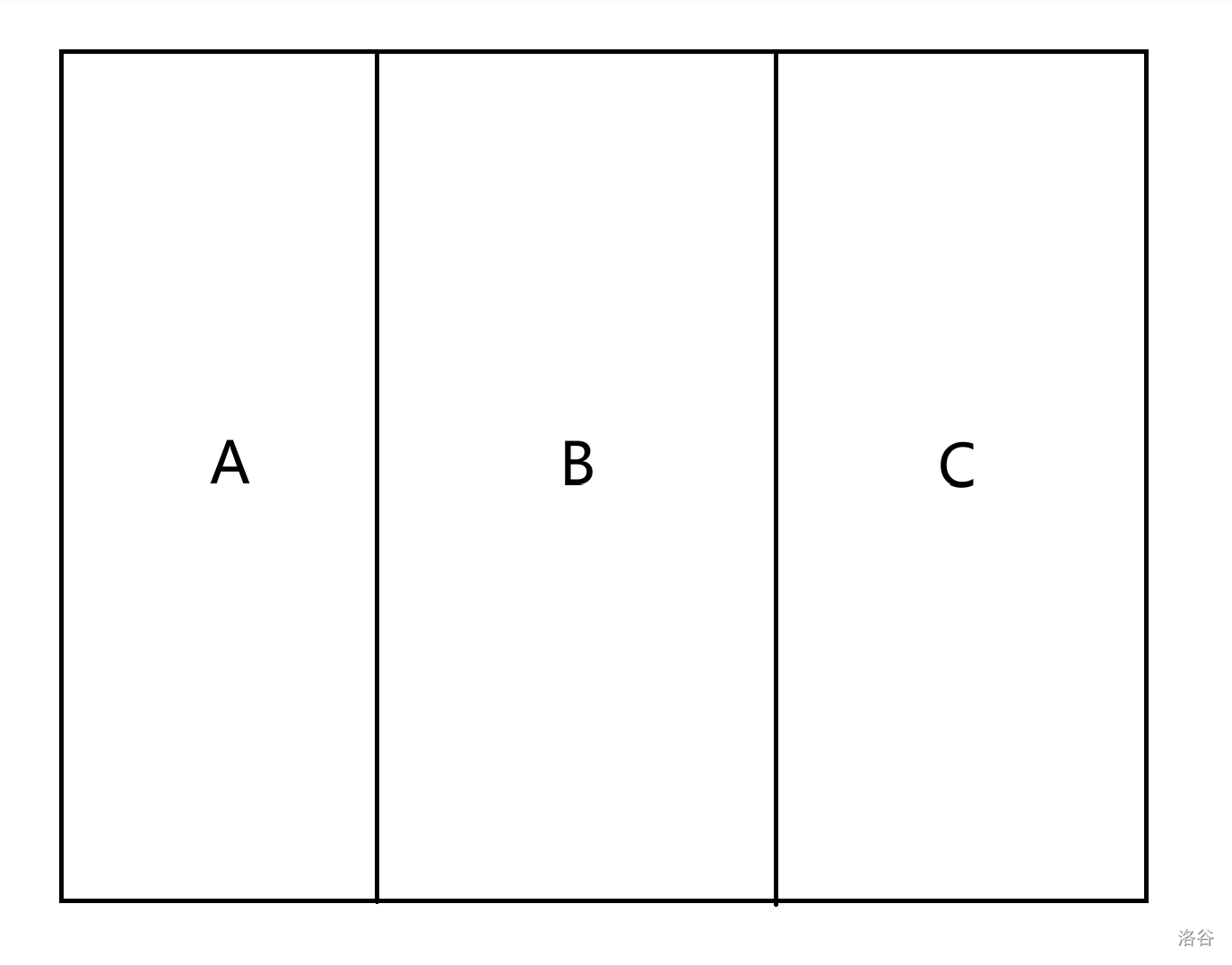
那么形如 ABC 这样的操作序列就会被 \(x_j\) 解决而不是 \(x_i\),三部分方案乘起来即可。
- 由 \(y_j (j<i)\) 得到。
这样会分成四块:
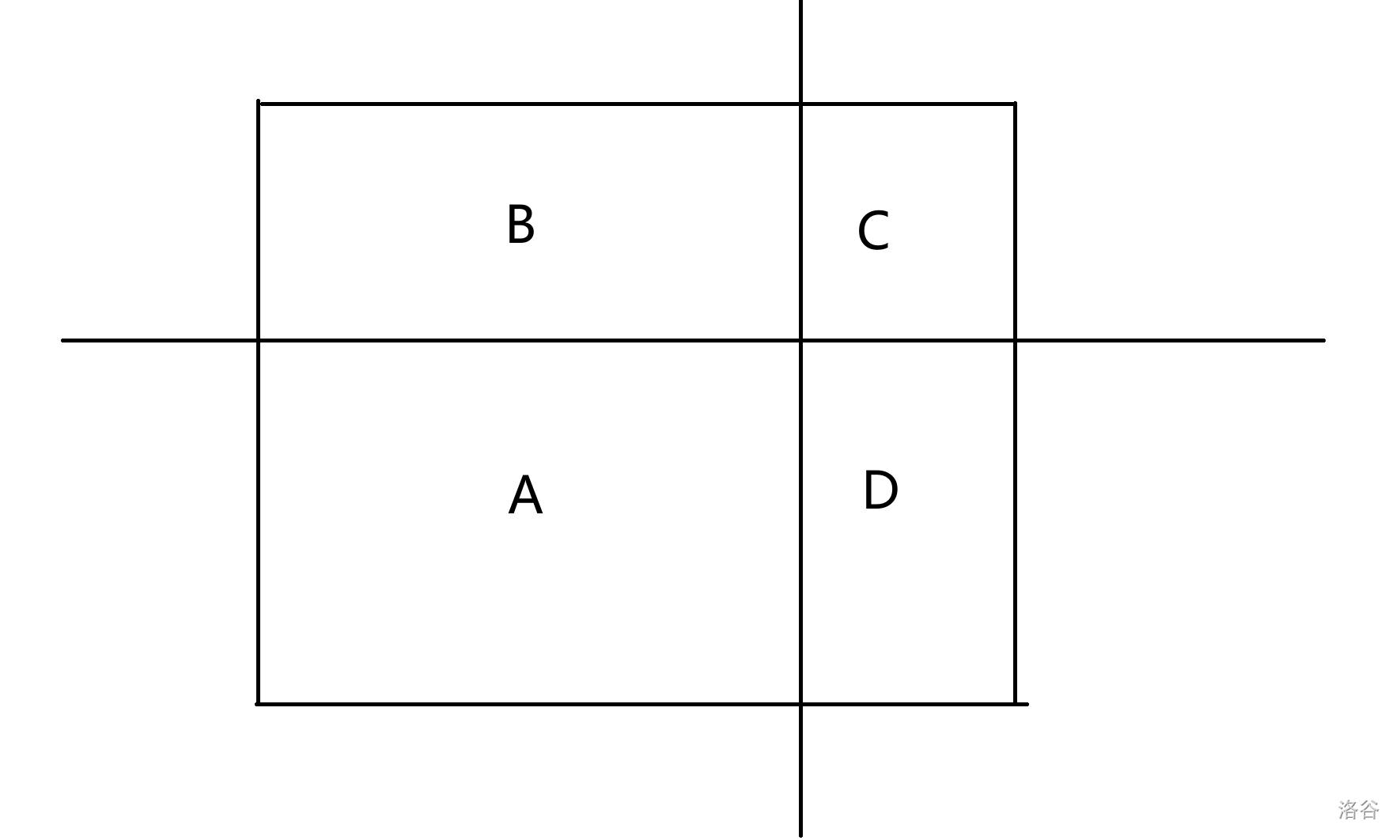
考虑 \(x_i,y_j\) 分别切出来的顺序会是怎样,\(x_i\) 会是 (AB)(DC),\(y_j\) 会是 (AD)(BC)。考虑什么时候会重复计算,发现只能是 \(D\) 为空的时候我们才会记重,所以就必须得满足 \(D\) 为空才会减去。
\(y\) 的同样讨论,读者可以自己推一下。
到这里已经可以写了,只不过写起来需要分讨很多。我们这里其实会发现一个事情,就是假设我们 \(x\in[l,r],y\in[u,d]\) 的矩形包含了集合为 \(S\) 的点,那么令 \(Tx_i\) 代表 \(x_i\) 下方切出来的部分,\(Ty\) 类似定义,那么我们考虑按照字典序扫描,那么只有前面的是后面的子集的时候才会被重复统计,其实感觉也是比较显然的。那么这样就可以比较方便地实现了。因为这些集合都是矩形交出来的,所以其实只有 \(O(n^4)\) 个,不用担心状态过多。
总复杂度 \(O(n^6)\)。
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 35, mod = 1e9 + 7;
int n, p[maxn], q[maxn];
map<int, int> mp;
int popcnt(int x) {int cnt = 0;while(x)cnt += x % 2, x >>= 1;return cnt;
}
int cnt = 0;
int cal(int s) {if(popcnt(s) <= 1)return mp[s] = 1;if(mp.count(s))return mp[s];
// cnt++;
// if(cnt <= 10)
// cout << s << endl;vector<int> x, y;for (int i = 1; i <= n; i++) {if((s >> i - 1) & 1)x.push_back(i), y.push_back(p[i]);} sort(y.begin(), y.end());vector<int> t;int nw1 = 0, nw2 = 0;for (int i = 0; i < x.size() - 1; i++) {nw1 |= (1 << x[i] - 1);t.push_back(nw1);nw2 |= (1 << q[y[i]] - 1);t.push_back(nw2);// if(cnt <= 5);// cout << s << " " << nw1 << " " << nw2 << endl;}vector<int> dp; dp.resize(t.size());int ans = 0;for (int i = 0; i < t.size(); i++) {dp[i] = cal(t[i]);for (int j = 0; j < i; j++)if((t[i] & t[j]) == t[j])dp[i] = (dp[i] - dp[j] * cal(t[i] ^ t[j]) % mod + mod) % mod;ans += dp[i] * cal(s ^ t[i]) % mod; ans %= mod;}
// cout << s << " " << ans << endl;return mp[s] = ans;
}
signed main() {cin >> n;for (int i = 1; i <= n; i++)cin >> p[i], q[p[i]] = i;cout << cal((1 << n) - 1) << endl;return 0;
}
