原题链接:https://artofproblemsolving.com/community/c4h3685828_1000th_post P1
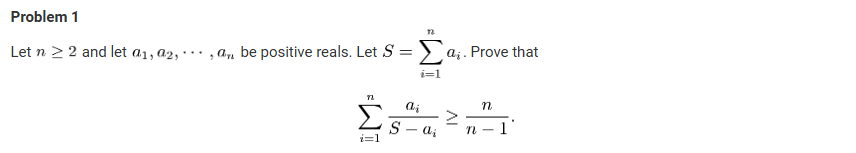
解法:
注意到有
\(\sum_{i=1}^n \frac{a_i}{s-a_i}=\sum_{i=1}^n\left(\frac{s}{b_i}-1\right)=\sum_{i=1}^n \frac{s}{b_i}+\sum_{i=1}^n-1\)
即
\(LHS=S \sum_{i=1}^n \frac{1}{b_i}-n\)
有
\(\begin{aligned} & S \sum_{i=1}^n \frac{1}{b_i}-n \geqslant \frac{n}{n-1} \\ & \sum_{i=1}^n S-a_i=\sum_{i=1}^n S-\sum_{i=1}^n a_i=S(n-1)\end{aligned}\)
所以
\(\frac{\sum_{i=1}^n b_i}{n}=S(n-1) \geqslant \frac{n}{\sum_{i=1}^n \frac{1}{b_i}}\)
代入待证,有
\(\begin{aligned} & \sum_{i=1}^n \frac{1}{b_i} \geqslant \frac{n^2}{s(n-1)} \\ & S\left(\frac{n^2}{S(n-1)}\right) \geqslant \frac{n}{n-1} \\ & n^2 \geqslant n\end{aligned}\) 显然成立
得证
