题意:很简单了,不再赘述。
做法:
先观察一下打打表,发现首先必须满足 \(a_i\equiv a_{i+\frac{N}2}\pmod {\frac{N}2}\),这里 \(N=2^n\),因为结束状态满足,且这两种操作都不影响他们对 \(\frac{N}{2}\) 取模的关系。
然后考虑我肯定是要让前 \(\frac{N}{2}\) 位的最高位要一样,变成 \(0\) 比较方便,我们就扫一遍,如果找到一个最高位为 \(1\) 的,那么就让他补全所有位再加一,这样就可以做到一个最高位取反的效果。
那么你可能会问这里为什么会保证不会影响其他的最高位呢,因为如果会影响,那么一定是满足他们两个模 \(\frac{N}2\) 同余,这样加一才能一起进位,但是显然是不存在的,所以不会影响到。
然后再用一次异或操作,将 \(a_0\) 变成 \(0\),其他的如果不是 \(a_i=i\) 那么就不可行。
但是这里其实还是可能可以用加一操作的,为什么我们不用考虑呢?
我们先讲如何实现,最后来解决这个问题。
跟位运算有关,大多可以拍到 Trie 树上来做,但是如果从高位往低位排不是很好做 \(+1\),我们考虑从低位往高位建立,这样 \(+1\) 就等于一条左链去 swap 左右儿子,然后就解决了,查询一个点就直接按点的编号向上跳即可,异或 \(x\) 就对 \(x\) 在二进制位上的 \(1\) 的位进行打标记即可。
那么来解释上面为什么不用 \(+1\) 的问题,我们发现最后我们要求的第 \(n-1\) 位一定是左儿子为前 \(\frac{N}{2}\) 位,但是如果 \(+1\) 就会打乱这个顺序,并且稍微手玩并理解一下,如果 \(+x\),第 \(p\) 位为 \(1\),那么就是从最右侧往左数第 \(p\) 组的儿子翻转了一下,可以看看图:
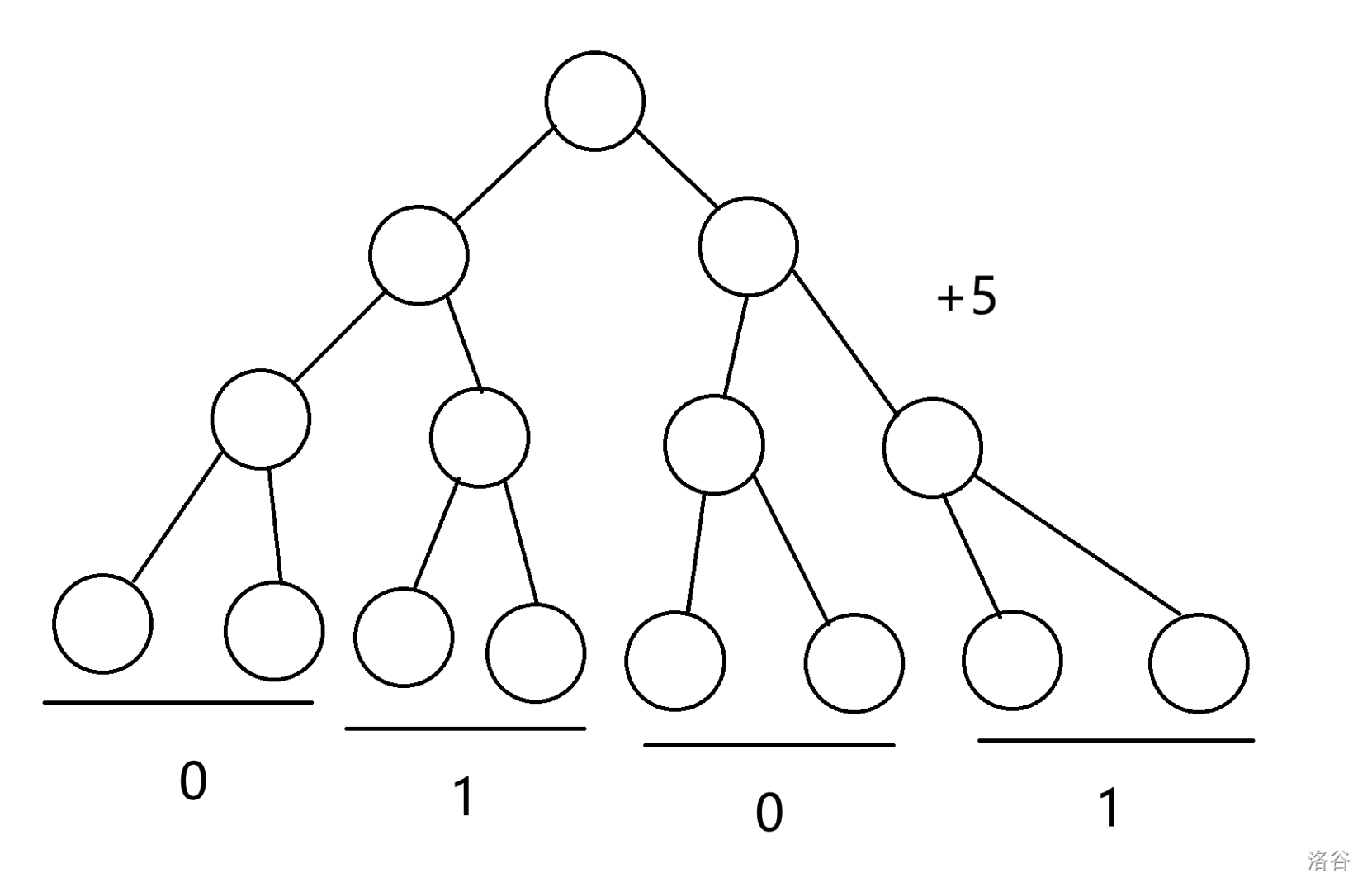
并且异或只是对整体一起交换,不会对底层内部交换,所以还是得靠加一才能交换内部,\(\frac{N}{2}\) 一个周期,但是显然是无意义的,所以只用考虑一次异或后是否合法就可以了。
代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn = (1 << 18) + 5;
struct node {int son[2], tag, fa;
} ;
vector<int> ans;
int n, N, a[maxn], p[maxn];
struct Trie {node tr[maxn << 2];int tot = 1, tag[maxn];int insert(int x) {int p = 1;for (int i = 0; i < n; i++) {int t = (x >> i) & 1;if(!tr[p].son[t])tr[p].son[t] = ++tot, tr[tot].fa = p;p = tr[p].son[t];}return p;}void make_xor(int x) {ans.push_back(x);for (int i = 0; i < n; i++)tag[i] ^= (x >> i) & 1;}void make_add() {int p = 1;for (int i = 0; i < n; i++) {swap(tr[p].son[0], tr[p].son[1]);if(tag[i])p = tr[p].son[1];elsep = tr[p].son[0];}ans.push_back(-1);}int query(int u) {int res = 0;for (int i = n - 1; i >= 0; i--) res += (tr[tr[u].fa].son[tag[i] ^ 1] == u) * (1 << i), u = tr[u].fa;return res;}
} tree;
int main() {cin >> n, N = (1 << n);for (int i = 0; i < N; i++)cin >> a[i];for (int i = 0; i < N / 2; i++)if(a[i] % (N / 2) != a[i + N / 2] % (N / 2)) {cout << "No" << endl;return 0;}for (int i = 0; i < N; i++)p[i] = tree.insert(a[i]);for (int i = 0; i < N / 2; i++) {int x = tree.query(p[i]);// cout << x << endl;if(x & (N / 2)) tree.make_xor(N - 1 - x), tree.make_add();}tree.make_xor(tree.query(p[0]));for (int i = 0; i < N; i++) if(tree.query(p[i]) != i) {cout << "No" << endl;return 0;}cout << "Yes" << endl;cout << ans.size() << endl;for (int i = 0; i < ans.size(); i++)cout << ans[i] << " ";cout << endl;return 0;
}
