树的性质
-
树上任意两点间恰有一条简单路径。
-
树上所有节点度数和为 \(O(n)\) 的。
-
树上 \(m\) 个点两两产生的 LCA 去重后不超过 \(m-1\) 个。
Proof:考虑找 LCA 的过程,两个点向上跳,重合时合并成一个点。最后剩下 \(1\) 个点,即合并了 \(m-1\) 次,故 LCA 最多有 \(m-1\) 个。
-
若 \(fa_i\) 在 \([1,i)\) 之间随机生成,则树高期望是 \(O(\log n)\)。
-
若树上无负权边,则所有直径中点交与一个点 / 一条边的中点。
-
若以一条边合并两棵树,则新的直径端点在原来的直径端点中产生。
-
到树上一个点距离最大的点,是某条直径的某个端点。
重心
-
树的中心一定有 \(1/2\) 个。
如果有 \(2\) 个重心,则它们相邻,且删除它们的连边后,生成的 \(2\) 个连通块大小相等。 -
以树的重心为根时,所有子树大小都不超过 \(\frac{n}{2}\)。
逆命题同样成立。 -
树上所有节点到某个点的距离和中,重心是最小的。
-
若以一条边合并两棵树,则新的重心一定位于连接原来两棵树重心的路径上,且一定在较大的树一侧(如果大小相同,则重心就是两个连接点)。
-
向树上增加 / 减少一个叶子,若原节点数为奇数,那么重心可能增加 \(1\) 个,原重心仍是重心;若原节点数为偶数,那么重心可能减少 \(1\) 个,另一个重心仍是重心。
题
QOJ14323 Reconstruct the tree
构造一棵 \(n\) 个节点的树,使其所有直径构成的集合与给定集合相等,或报告无解。
\(n\le 2\cdot 10^5\)。
P8089 『JROI-5』Color
先考虑朴素的 DP,令 \(f_u\) 为 \(u\) 作根节点的答案,则有转移 \(f_u=(f_l+1)(f_r+1)\)。
这样做是 \(O(2^n)\) 的。但我们发现,根节点必定有一个子树是满的,沿着那个不满的子树向下走,到达的子节点仍然满足这个条件……
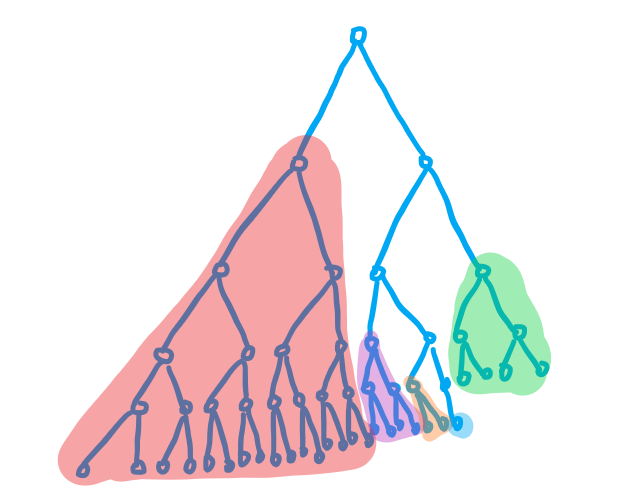
而我们知道,计算满二叉树的答案十分简单,只需要根据上面的递推式来跑,就能预处理出高度为 \(1,2,\dots\) 的满二叉树的答案。然后就做完了。
时间复杂度 \(O(T\cdot dep)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5,P=998244353;
int t,n,g[N],f[N],ans=1;
string s;
bitset<N> a;
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);g[1]=1;for(int i=2;i<N;i++) g[i]=(g[i-1]+1)*(g[i-1]+1)%P;cin>>t;while(t--){cin>>n>>a;if(a[n-1]==1){cout<<g[n]<<"\n";}else{ans=0;for(int i=n-2;~i;i--){if(a[i]) f[i]=g[i+1]+1;else f[i]=g[i]+1;}for(int i=0;i<n-1;i++) ans=(ans+1)*f[i]%P;cout<<ans<<"\n";}}return 0;
}
CF1764F Doremy's Experimental Tree
现有一个 \(n\) 个节点,有边权的树,边权 \(\in[1,10^9]\)。
选定节点 \(i,j\),并在 \(i,j\) 之间添加一条权值为 \(1\) 的边,此时图中会出现一个环,定义 \(f(i,j)\) 为所有节点到环的最短路之和。
现在告诉你所有的 \(f(i,j)\),请复原这棵树的结构和边权。
\(n\le 2000\)。
不妨规定 \(1\) 为根节点。
不难发现如果 \(f(1,v)>f(1,u)\),\(v\) 必定在子树 \(u\) 之外。
进一步观察可得,这样的 \(v\) 中,使 \(f(u,v)\) 最大的 \(v\) 就是 \(u\) 的父节点。
因此可以确定树的结构。接下来考虑如何确定边权。
对于 \((u,fa_u)\) 这条边,我们发现 \(f(u,u)\) 相对 \(f(u,fa_u)\) 减少的量,就是 \(w(u,fa_u)\times{}\)子树 \(u\) 以外的节点个数。
原因是子树 \(u\) 以外的节点原来需要走到 \(u\),现在只需要走到 \(fa_u\) 就可以了,一共少走了 \((n-siz_u)\times w(u,fa_u)\) 的权值。
所以 \(w(u,fa_u)=\cfrac{f(u,u)-f(u,fa_u)}{(n-siz_u)}\)。
时间复杂度 \(O(n^2)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2002,inf=1e18;
int n,f[N][N],fa[N],siz[N];
vector<int> G[N];
void dfs(int u){siz[u]=1;for(int i:G[u]){dfs(i);siz[u]+=siz[i];}
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>f[i][j];f[j][i]=f[i][j];}}for(int i=2;i<=n;i++){int mx=-inf;for(int j=1;j<=n;j++){if(f[1][j]>f[1][i]&&f[i][j]>mx){mx=f[i][j];fa[i]=j;}}G[fa[i]].emplace_back(i);}dfs(1);for(int i=2;i<=n;i++){cout<<i<<" "<<fa[i]<<" "<<(f[i][i]-f[i][fa[i]])/(n-siz[i])<<"\n";}return 0;
}
Gym104976F Top Cluster
给定 \(n\) 个节点的树,有点权和边权,保证点权互不相同。\(q\) 次询问,每次给定 \(x,k\),求到 \(x\) 距离不超过 \(k\) 的点的权值构成的 \(\text{mex}\)。
一个集合的 \(\text{mex}\) 定义为不在其中的最小非负整数。
所有权值 \(\le 10^9\),\(n,q\le 5\cdot 10^5\)。
由于点权互不相同,所以所求可以转化为“所有点权的 \(\text{mex}\)”与“到 \(x\) 距离 \(>k\) 的最小点权”取最小值。
前者可以预处理,后者考虑二分答案。
即转化为计算“点权 \(\le mid\) 的点到 \(x\) 的最大距离是否 \(>k\)”。
根据树的性质,最大距离只能在 \(x\) 与直径的两端点之一取到。
因此我们可以处理点权前 \(1,2,\dots n\) 大的点所组成的直径 \((u_1,v_1),\dots,(u_n,v_n)\)。具体来说,令点权第 \(i\) 大的点为 \(x\),则 \(u_i,v_i\) 一定取自 \(u_{i-1},v_{i-1},x\) 这三个值,用 LCA 来两两计算距离,取最大即可。
好像这道题必须用 \(O(1)\) 查询的 LCA,遂采取 DFS 序求法。
时间复杂度 \(O((n+q)\log n)\)。
不知道为什么一直 WA on #23,暂且不调了。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+5,inf=1e18;
int n,q,head[N],idx,dfn[N],tim,mi[20][N],d[N],mex;
struct Node{int id,w;}a[N];
struct Path{int u,v;}s[N];//直径
struct Edge{int nxt,to,w;}e[N<<1];
inline void add(int u,int v,int w){e[++idx]={head[u],v,w},head[u]=idx;}
inline int get(int x,int y){return dfn[x]<dfn[y]?x:y;}
void dfs(int u,int f){mi[0][dfn[u]=++tim]=f;for(int i=head[u];i;i=e[i].nxt) if(e[i].to!=f)d[e[i].to]=d[u]+e[i].w,dfs(e[i].to,u);
}
inline int LCA(int u,int v){if(u==v) return u;if((u=dfn[u])>(v=dfn[v])) swap(u,v);int d=__lg(v-u++);return get(mi[d][u],mi[d][v-(1<<d)+1]);
}
inline int dis(int u,int v){if(!u||!v) return -inf;return d[u]+d[v]-(d[LCA(u,v)]<<1);
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n>>q;for(int i=1;i<=n;i++) cin>>a[i].w,a[i].id=i;for(int i=1,u,v,w;i<n;i++){cin>>u>>v>>w;add(u,v,w),add(v,u,w);}dfs(1,0);for(int i=1;i<=__lg(n);i++)//LCA 预处理for(int j=1;j+(1<<i)-1<=n;j++)mi[i][j]=get(mi[i-1][j],mi[i-1][j+(1<<(i-1))]);sort(a+1,a+1+n,[](Node a,Node b){return a.w<b.w;});mex=n;for(int i=1;i<=n;i++) if(a[i].w!=i-1){mex=i-1;break;}for(int i=1;i<=n;i++){int x=a[i].id,a[3]{dis(x,s[i-1].u),dis(x,s[i-1].v),dis(s[i-1].u,s[i-1].v)},mx=max({a[0],a[1],a[2]});if(mx==a[0]) s[i]={x,s[i-1].u};else if(mx==a[1]) s[i]={x,s[i-1].v};else s[i]={s[i-1].u,s[i-1].v};}int x,k;while(q--){cin>>x>>k;int l=1,r=mex;while(l<r){int mid=(l+r)>>1;if(max(dis(x,s[mid].u),dis(x,s[mid].v))>k) r=mid;else l=mid+1;}cout<<a[l].w<<"\n";}return 0;
}
