光栅化
Rasterrization—光栅化(三角形的离散化)
屏幕(Screen)在图形学我们可以被抽象为一个二维数组,其中二维数组中的每个元素是像素( pixel )。
屏幕空间(screen space)是由数组构成的平面坐标系,每一个像素用坐标表示,像素的中心在x+0.5和y+0.5上。
为了把单位立方体里面的所有物体画在屏幕上(Canonical Cube to Screen)我们首先必然要做一个视口变换,要得到视口变化矩阵(Viewport transform matrix),原来我们单位立方体的x和y都是2,现在x要变成width那就需要乘width /2,而y要变成height那就需要乘height/2,而z保持不变则为1(这个z值后面会详细介绍用来做深度测试),还需要平移(width /2,height/2)个单位(概括为先缩放再平移)。这样我们就可以算出视口变化矩阵(Viewport transform matrix)(如下图):
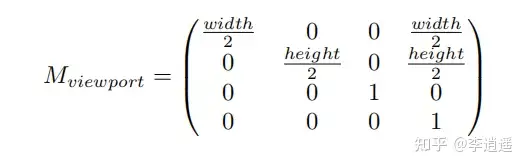
视口变化矩阵(Viewport transform matrix)
通过视口变化矩阵(Viewport transform matrix)把单位立方体映射到屏幕空间(如下图)
xy平面中的变换: [-1, 1]2 to [0, width] x [0, height]
到这一步的时候大家不要忘了我们此时得到的不过是屏幕空间中的一些三角而已,但是这远远不够我们需要把这些三角形打碎打成像素并且告诉每个像素的值是多少然后显示在屏幕上,这一个完整的过程我们称之为光栅化(Rasterization)。
三角形在图形学中可以看做是几何体的基本形状(Triangles - Fundamental Shape Primitives),三角形在图形学中有很多很好的性质:
- 三角形是最基本的多边形,并且任何其他的多边形都可以拆分为三角形。
- 三个点可以保证他在一个平面如果是四边形四个点就不能保证。
- 它可以很好地用叉积判断一个点是不是在三角形内部(三角形的内外定义特别清晰)[4]。
Sampling—(采样)
采样的概念
采样就是给定一个连续的函数,在不同的点求它的值,也可以认为,采样是把一个连续的函数离散化的过程。
采样是指利用像素的中心对屏幕空间进行采样,采样不仅可以在空间上采样,还可在时间上采样。因此需要定义一个 inside(tri, x, y)函数,使用叉乘判断这个像素的中心是否在三角形内,如果这个点一直在三角形三条边的左边或右边那么就可以认为这个点在这个三角形的内部。
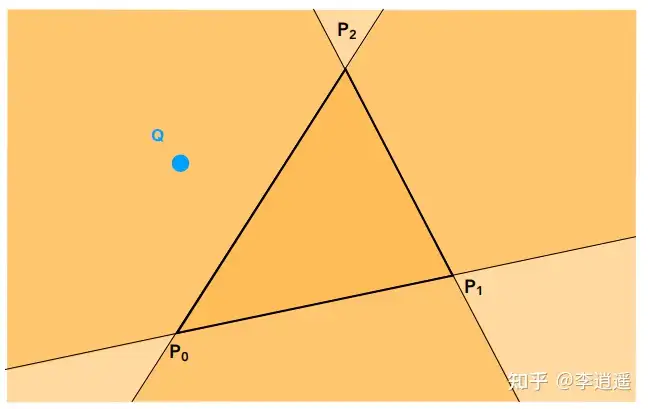
如果这个点在三角形的内部那么我们就定义它为1,不在内部就定义为0(这里的像素只考虑是显示还是不显示的问题,不考虑像素内部颜色的变化)。这样我们就可以确定inside(tri, x, y)这个函数了(如下图)
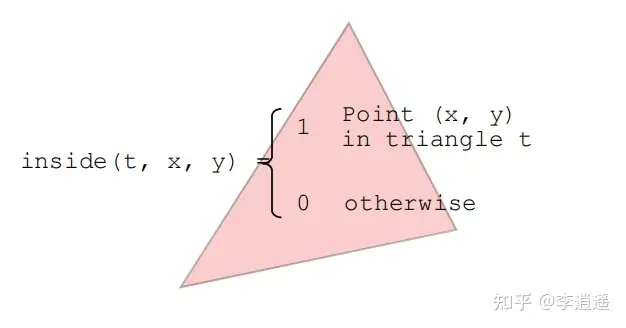
接下来就是遍历整个屏幕中的像素,然后判断像素的中心点是否在三角形内部,如果在就赋值为1并显示。

遍历整个屏幕空间的像素太浪费了,因为三角形可能只是屏幕中很小的一部分,因此可以进一步优化,只要判断这个三角形包围盒里面的像素就可以了(如下图)
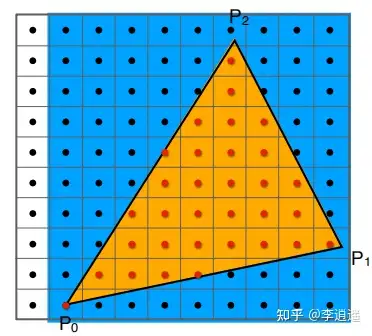
采样优化的一种:对三角形包围盒里面的函数进行采样
采样中的Artifacts(瑕疵)
锯齿
采样完成后,我们自然知道有哪些像素的中心点在三角形内,那我们自然而然的可以把这些像素填成三角形对应的颜色,我们又知道像素是一个小方块并且它内部的颜色是均匀的,所以下图左边三角形内的像素中心点对应在不同的像素上会变成右边这样(如下图)
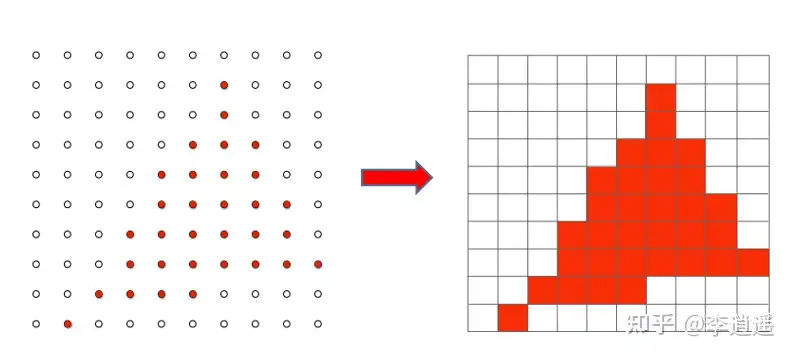
这样我们就会发现一个问题,我们想要得到的是一个三角形,但是实际得到的不完完全是一个三角形,不过的它的形状和三角形大概类似,这就是我们所说的锯齿(Jaggies!)。有两个原因导致锯齿:一是像素本身有一定的大小,二是采样的速度更不上信号变化的速度(高频信号采样不足)。
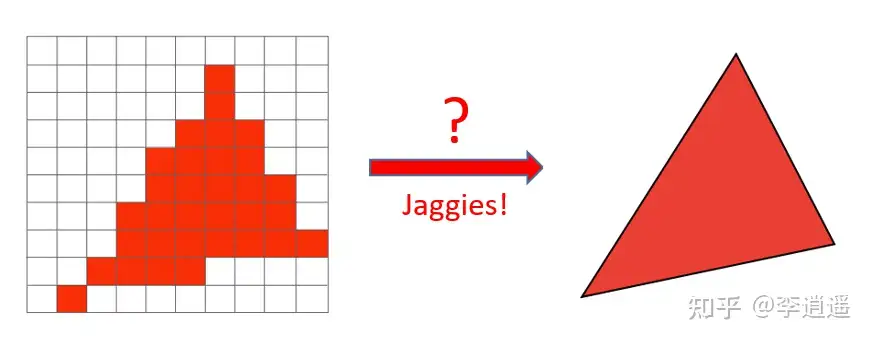
Sampling Artifacts in Computer Graphics—(采样所产生的瑕疵)
前面我们已经知道,采样在图形学中广泛存在。光栅化的过程其实就是在屏幕空间离散的像素中心点上进行采样来判断像素是否在三角形内的采样。
一张照片其实就是所有达到感光元件的光学信息,通过把它离散成图像的过程,其实这也是采样。采样不仅可以发生在不同的位置,也可以发生在不同的时间,视频就是在时间中进行采样的。因此采样是广泛存在的,同样采样带来的问题也是广泛存在的。
采样产生的第一个问题就是我们刚刚提到的锯齿问题(Jaggies)
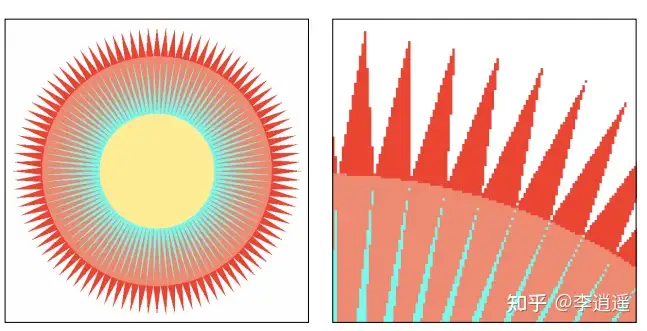
摩尔纹
