一、基本概念
【发点和收点】设点 v 是有向图 D (带箭头)的一个顶点:
1、发点:如果不存在以v为终点的弧,则称v是D的一个发点(源),通常称为vs;
2、收点:如果不存在以v为始点的弧,则称v是D的一个收点(汇),通常称为vt。
【容量和流量】
1、容量:网络中某条弧(vi,vj)的最大通过能力称为该弧的容量,记做 cij ;
2、流量:通过弧 (vi,vj)的某种流的实际数量称为该弧的流量,记做 fij 。
【可行流和最大流】
发点 vs流出的流量为 f ,则汇入收点vt的流量为 -f。这个f,就是可行流。如果一个网络图中,有n个发点,n个收点,那么可行流就是所有发点发出流量的和,也就是所有收点收到流量的和。
可行流具备以下两个特征:
1、可行性条件:对每一条弧 (vi , vj )∈ A ,均应有,0 ≤ fij ≤ cij。即每条弧的流量,都应该是非负的,是大于等于0,且小于这条弧的容量的;
2、平衡条件:除了发点和收点,其余点都是中间点,可以理解为中转站。流入任何一个中间点的流量必等于流出该顶点的流量,即对 vi ≠ vs , vt时:
因此对于可行流 f 来说,对发点,它的公式就是如下形式。对于收点就是 -f :

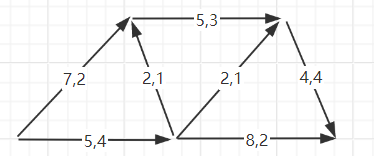
示例:下面的网络图,每个弧,弧旁第一个数字为容量,第二个数字为流量,即 cij, fij。每条弧都满足非负性和中间点的平衡条件,因而为一可行流,且可行流 f = 6(发流量为2+4)。这里有一个特殊的情况,即,可能存在某条弧完全没有启动,或者整个网络为初始状态,这时候就会有零流 fij= 0,它一定是一个可行流。因而在一个网络图中,可行流总是存在的,至少有零流。
【网络的最大流】
在一张网络中,每条弧容量不同,走每条弧的成本不同,因此,不同的规划,得到的可行流的流量,并不相同。找到最大的可行流,也就是找到网络的最大流,是很多实际问题需要的。这也是一个线性规划问题,可描述为:

