Day 25
第七章 回溯算法 part04
491.递增子序列
本题和大家刚做过的 90.子集II 非常像,但又很不一样,很容易掉坑里。
https://programmercarl.com/0491.递增子序列.html
视频讲解:https://www.bilibili.com/video/BV1EG4y1h78v
回溯三部曲
-
递归函数参数
求子序列,因此一个元素不能重复使用,需要startIndex -> 去调整下一层递归的其实位置
-
终止条件
本题类似求子集问题,要遍历树形结构找每个节点。因此可不加终止条件。
startIndex每次都会加1,并不会无限递归。
注意:本题收集结果要求->递增子序列大小至少为2
-
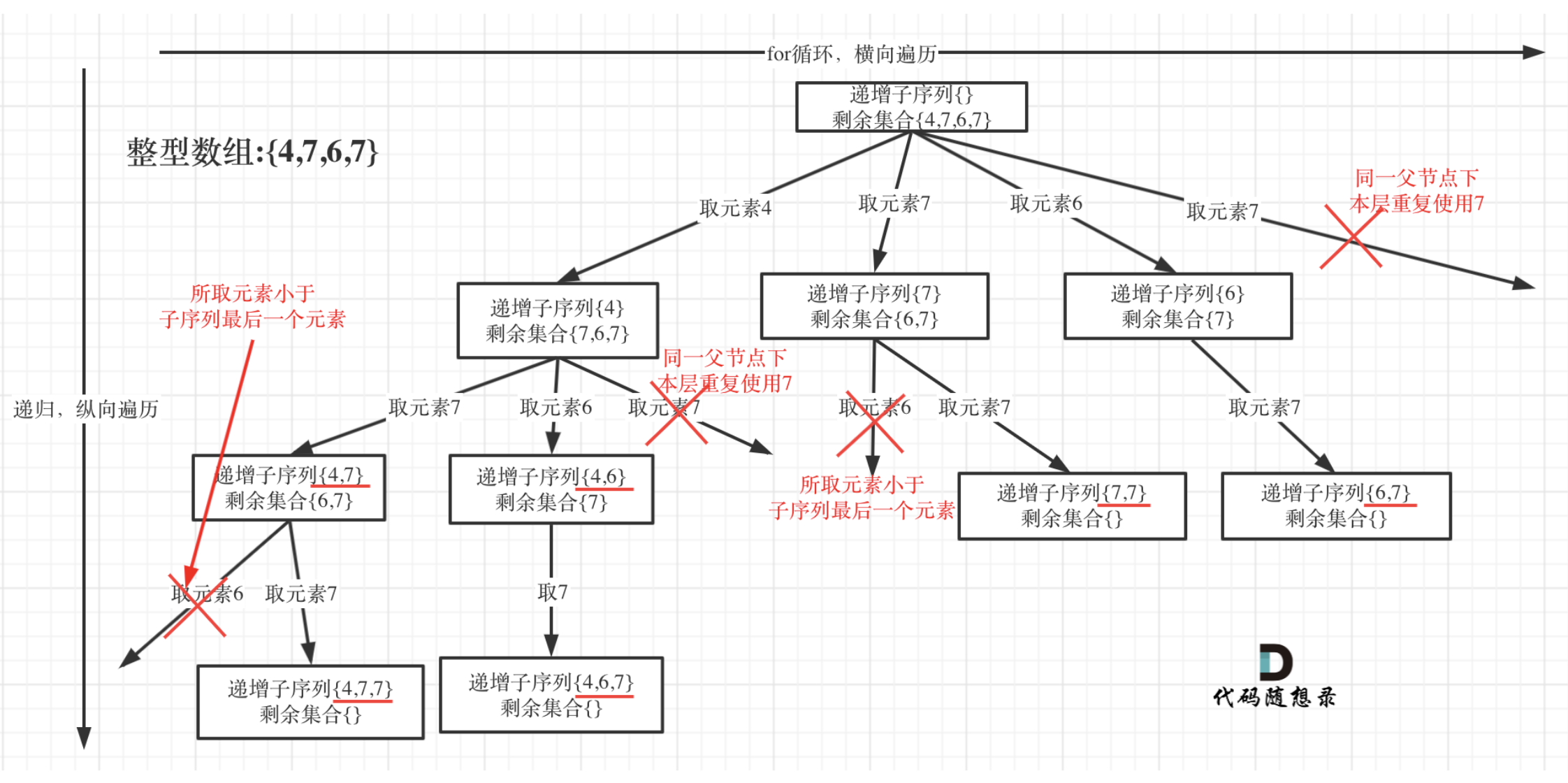
单层搜索逻辑
同一父节点下的同层上使用过的元素就不能再使用了
![img]()
class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backtracking(nums,0);return result;}private void backtracking(int[] nums, int startIndex){if (path.size() >= 2){result.add(new ArrayList<>(path));}HashSet<Integer> hs = new HashSet<>();for(int i=startIndex;i<nums.length;i++){if (!path.isEmpty() && path.get(path.size()-1) >nums[i] || hs.contains(nums[i])){continue;}hs.add(nums[i]);path.add(nums[i]);backtracking(nums, i+1);path.remove(path.size()-1);}}
📌 代码解析
class Solution {List<List<Integer>> result = new ArrayList<>(); // 存放所有符合要求的子序列List<Integer> path = new ArrayList<>(); // 存放当前递归路径(一个候选子序列)public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums, 0); // 从下标0开始递归return result;}private void backTracking(int[] nums, int startIndex){// 只要当前子序列长度 ≥ 2,就加入结果集if(path.size() >= 2)result.add(new ArrayList<>(path)); // 用 HashSet 记录本层递归用过的数字,避免重复HashSet<Integer> hs = new HashSet<>();// 遍历当前层所有选择for(int i = startIndex; i < nums.length; i++){// 剪枝条件:// 1. 必须保持非递减:path 最后一个元素 > 当前元素 -> 不符合// 2. 本层已经用过相同数字 -> 跳过if(!path.isEmpty() && path.get(path.size() - 1) > nums[i] || hs.contains(nums[i]))continue;// 本层没用过这个数字,加入 seths.add(nums[i]);// 做选择path.add(nums[i]);// 递归:继续往后选backTracking(nums, i + 1);// 撤销选择path.remove(path.size() - 1);}}
}
📌 思路解释(和 Python 对比)
Java 和 Python 的主要区别在语法和数据结构:
-
List 声明
- Java:
List<Integer> path = new ArrayList<>(); - Python:
path = []
- Java:
-
拷贝列表
- Java:
new ArrayList<>(path) - Python:
path[:]
- Java:
-
集合去重
- Java:
HashSet<Integer> hs = new HashSet<>(); - Python:
used = set()
- Java:
-
取列表最后一个元素
- Java:
path.get(path.size() - 1) - Python:
path[-1]
- Java:
-
删除最后一个元素
- Java:
path.remove(path.size() - 1) - Python:
path.pop()
- Java:
📌 Java 写法需要注意的地方
-
类型明确:
Java 必须写清楚List<Integer>,不像 Python 动态类型随便用。 -
深拷贝:
new ArrayList<>(path)等价于 Python 的path[:]。否则会被引用修改。 -
递归函数声明:
Java 需要写成private void backTracking(int[] nums, int startIndex),不能像 Python 那样随便定义。 -
逻辑运算符:
- Java 的
||等价于 Python 的or - Java 的
&&等价于 Python 的and
- Java 的
📌 总结
[] → ArrayList<>set() → HashSet<>()list[:] → new ArrayList<>(list)list.pop() → list.remove(list.size()-1)
Java 的 List 是引用类型,如果直接写:
result.add(path);
其实是把 path 的引用 加进了 result。
这样会出现什么情况呢?
⚠️ 举个例子
假设 nums = [4,6],递归过程:
-
一开始
path = [] -
选
4→path = [4] -
选
6→path = [4,6]- 如果
result.add(path),此时 result 里放进去的是 引用,指向同一个path。 - result =
[ [4,6] ]
- 如果
-
回溯,撤销
6→path = [4]- 注意:因为 result 里保存的不是拷贝,而是指针,所以 result 里的内容也变成
[4]了 - result =
[ [4] ]❌(不符合要求)
- 注意:因为 result 里保存的不是拷贝,而是指针,所以 result 里的内容也变成
等最后递归完毕,result 里保存的会是 一堆空列表或者被修改过的 path,而不是每一步的快照。
✅ 正确做法
所以必须要写:
result.add(new ArrayList<>(path));
new ArrayList<>(path) 会新建一个 新的列表对象,并把当前 path 里的元素复制过去。
这样即使 path 后面被回溯修改了,result 里已经保存了一个独立的快照,不会受到影响。
📌 对比 Python
在 Python 里写:
res.append(path)
也会遇到同样问题。
所以一般都写:
res.append(path[:]) # 切片拷贝
Java 的 new ArrayList<>(path) 就是 Python 的 path[:]。
Java 里这几个常见的数据结构
1. int[] —— 数组
-
定义:固定长度的数组,类型必须一致。
-
特点:长度一旦创建就不能改变。
-
语法:
int[] arr = new int[5]; // 长度为5的数组,默认值都是0 int[] nums = {1, 2, 3}; // 声明 + 初始化 System.out.println(nums[0]); // 访问元素,输出1 -
Python 类比:
list,但注意 Java 的数组长度固定,Python list 可以动态扩展。
2. List —— 接口(抽象类型)
-
定义:Java 里
List是一个接口,规定了“有序集合”应该支持的操作,比如add()、get()、remove()等。 -
特点:
- 是抽象的,不能直接
new List<>() - 必须用它的实现类,比如
ArrayList、LinkedList
- 是抽象的,不能直接
-
语法:
List<Integer> list = new ArrayList<>(); list.add(10); list.add(20); System.out.println(list.get(0)); // 输出10 -
好处:用
List声明变量,可以随时切换底层实现(ArrayList/LinkedList),更灵活。 -
Python 类比:Python 里没有接口的概念,但
list就相当于 Java 的List功能。
3. ArrayList —— List 的常用实现类
-
定义:基于动态数组实现的
List。 -
特点:
- 支持动态扩容,类似 Python 的
list.append()。 - 查询(
get(i))效率高:O(1) - 插入/删除效率低:O(n),因为要移动后面的元素
- 支持动态扩容,类似 Python 的
-
语法:
ArrayList<Integer> arrList = new ArrayList<>(); arrList.add(1); // 添加 arrList.add(2); arrList.remove(0); // 删除下标0的元素 System.out.println(arrList); // [2] -
Python 类比:Python 的
list。
4. HashSet —— 集合(无序、不重复)
-
定义:基于哈希表实现的集合。
-
特点:
- 元素不重复
- 元素无序(不像
List有下标) - 查询、插入、删除效率都接近 O(1)
-
语法:
HashSet<Integer> set = new HashSet<>(); set.add(1); set.add(2); set.add(1); // 重复元素不会加入 System.out.println(set); // [1, 2],顺序不保证 -
Python 类比:Python 的
set
📊 总结对比表
| Java | 含义 | Python 对应 | 是否可变 | 是否允许重复 | 是否有序 |
|---|---|---|---|---|---|
int[] |
固定长度数组 | list |
❌长度固定 | ✅允许重复 | ✅有序 |
List |
接口,抽象定义 | - | - | - | - |
ArrayList |
动态数组实现的 List | list |
✅可变 | ✅允许重复 | ✅有序 |
HashSet |
哈希集合 | set |
✅可变 | ❌不允许重复 | ❌无序 |
46.全排列
本题重点感受一下,排列问题 与 组合问题,组合总和,子集问题的区别。 为什么排列问题不用 startIndex
https://programmercarl.com/0046.全排列.html
视频讲解:https://www.bilibili.com/video/BV19v4y1S79W
回溯三部曲
-
递归函数参数
排列是有序的,因此[1, 2]和[2, 1]是两个集合
这道题也没办法用startIndex,需要用到一个used数组,标记已经选择的元素
-
递归终止条件
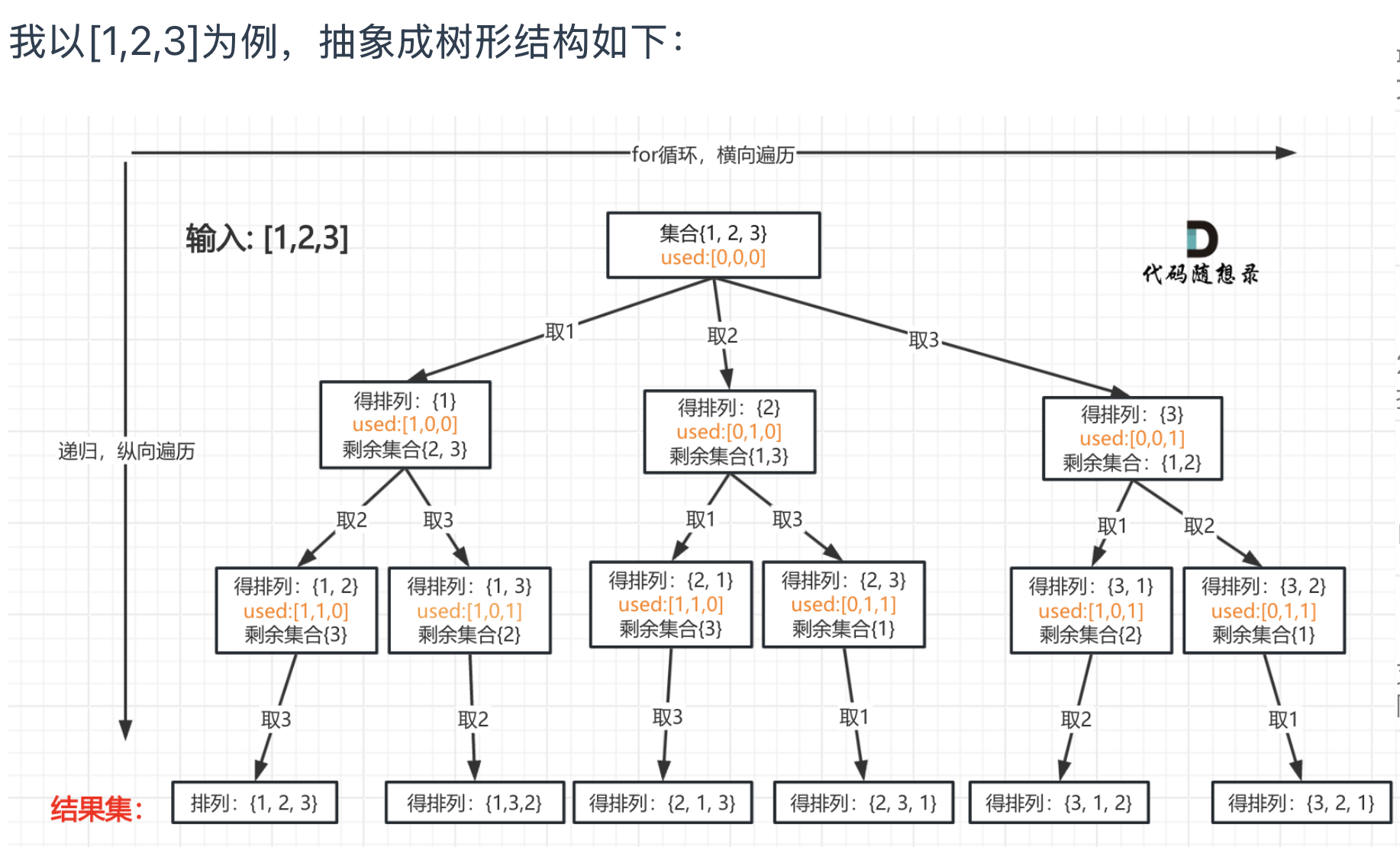
![img]()
根据此图可知,到达叶子结点,就是收割结果的地方
到达叶子结点 -> 当收集元素的数组path的大小达到和nums数组一样大的时候,说明找到了一个全排列,也表示到达了叶子节点。
-
单层搜索的逻辑
这里不用startIndex了。
因为排列问题,每次都要从头开始搜索。
used数组记录此时path里都有哪些元素使用了,一个排列里一个元素只能用一次。
class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> permute(int[] nums) {if (nums.length == 0){return result;}backtracking(nums, path);return result;}public void backtracking(int[] nums, LinkedList<Integer> path){if (nums.length == path.size()){result.add(new ArrayList<>(path));return;}for(int i = 0; i < nums.length; i++){if (path.contains(nums[i])){continue;}path.add(nums[i]);backtracking(nums,path);path.removeLast();}}
}
📌 代码逐行解析
class Solution {List<List<Integer>> result = new ArrayList<>(); // 存放所有结果LinkedList<Integer> path = new LinkedList<>(); // 存放当前排列的路径public List<List<Integer>> permute(int[] nums) {if (nums.length == 0) return result;backtrack(nums, path);return result;}public void backtrack(int[] nums, LinkedList<Integer> path) {// 递归出口:如果当前路径长度等于nums长度,说明形成了一个完整排列if (path.size() == nums.length) {result.add(new ArrayList<>(path)); // 加一个拷贝return;}// 遍历所有选择for (int i = 0; i < nums.length; i++) {// 如果当前数字已经在path里了,跳过if (path.contains(nums[i])) {continue;}// 做选择path.add(nums[i]);// 递归:继续构造下一个位置backtrack(nums, path);// 撤销选择path.removeLast();}}
}
📌 解题思路
-
回溯法框架
-
回溯的基本结构:
- 做选择
- 递归
- 撤销选择
-
-
path 的作用
path存储当前递归路径,也就是“正在生成的排列”。- 当
path.size() == nums.length,说明生成了一个完整排列 → 加入结果集。
-
如何避免重复选择?
-
每次循环时,用
if (path.contains(nums[i]))检查:- 如果当前数字已经在
path中,就跳过。
- 如果当前数字已经在
-
这样保证每个数字只出现一次。
-
-
为什么用
removeLast()?LinkedList提供了removeLast(),效率比remove(path.size()-1)更高。- 等价于 Python 里的
path.pop()。
-
拷贝
path- 必须写成
new ArrayList<>(path),而不是直接result.add(path),原因和前面你问的一样:Java 的集合是引用,直接加会被后续修改污染。
- 必须写成
📌 运行示例
以 nums = [1,2,3] 为例:
递归树大概是这样的:
[]
├── [1]
│ ├── [1,2]
│ │ └── [1,2,3] ✅
│ └── [1,3]
│ └── [1,3,2] ✅
├── [2]
│ ├── [2,1]
│ │ └── [2,1,3] ✅
│ └── [2,3]
│ └── [2,3,1] ✅
└── [3]├── [3,1]│ └── [3,1,2] ✅└── [3,2]└── [3,2,1] ✅
最后 result 收集到所有 6 个排列。
上面那份代码里用的是:
if (path.contains(nums[i])) {continue;
}
这意味着:只要 path 里已经出现过这个数,就不会再选。
这没问题的前提是 —— 输入数组 nums 里没有重复元素。
📌 情况一:没有重复元素
比如 nums = [1,2,3]
- 递归时,path 里一旦有
1,就不会再选1 - 因为数组本来就只有一个
1,所以这样正好。
这就是 LeetCode 46 (Permutations),输入保证无重复。
📌 情况二:有重复元素
比如 nums = [1,1,2]
如果你还用 path.contains(),就会出错:
- 第一次选
nums[0] = 1,放进 path - 遍历到
nums[1] = 1,path.contains(1)返回 true,就跳过了 - 结果就丢失了用第二个
1的情况
所以这种写法 不能处理重复元素。
📌 解决办法
如果题目允许数组有重复元素(LeetCode 47 Permutations II),我们要更细致地区分:
-
是否用过某个位置(而不是值)
- 用一个
boolean[] used标记每个下标是否已被选择过 - 这样就能区分第一个
1和第二个1
- 用一个
-
如何避免结果重复?
-
常用方法是 先排序,再加一条剪枝逻辑:
if (i > 0 && nums[i] == nums[i-1] && !used[i-1]) {continue; } -
这表示:如果当前数和前一个数相同,且前一个数还没被用过,那么跳过,避免重复排列。
-
📌 对比两种题目
-
全排列 I (LeetCode 46)
- 输入无重复元素
- 用
path.contains()或boolean[] used都行
-
全排列 II (LeetCode 47)
- 输入可能有重复元素
- 必须用
boolean[] used - 还要加额外剪枝,防止重复解
两道题(递增子序列 和 全排列)里 path 用 ArrayList 还是 LinkedList,并不是硬性规定,而是出于方便和习惯的选择。我们拆开讲:
📌 ArrayList 和 LinkedList 的区别(简单回顾)
-
ArrayList
- 底层是动态数组
- 随机访问快(
get(i)是 O(1)) - 在尾部增删也还行(均摊 O(1))
- 在中间插入/删除慢(O(n))
-
LinkedList
- 底层是双向链表
- 插入/删除快(只改指针 O(1))
- 随机访问慢(
get(i)是 O(n)) - 但支持
addLast()、removeLast(),写起来很简洁
📌 在回溯题里的用法
1. 递增子序列 (Increasing Subsequences)
List<Integer> path = new ArrayList<>();
为什么用 ArrayList?
- 需要经常取最后一个元素:
path.get(path.size()-1) - 需要复制快照:
new ArrayList<>(path) ArrayList在这种场景下比LinkedList更自然- Python 里你写
path[-1],其实和ArrayList的访问方式更像
2. 全排列 (Permutations)
LinkedList<Integer> path = new LinkedList<>();
为什么用 LinkedList?
-
每次只在尾部操作:
- 添加元素:
path.add(nums[i]) - 删除最后一个元素:
path.removeLast()
- 添加元素:
-
LinkedList提供了现成的removeLast()方法,写起来比ArrayList的remove(path.size()-1)更简洁直观。
📌 其实可以互换吗?
完全可以。
这两题里 用 ArrayList 或 LinkedList 都能过,区别主要是:
ArrayList→ 访问元素方便 (get(i))LinkedList→ 尾部删除方便 (removeLast())
所以很多题解写法不同,是因为 习惯 + 代码简洁度。
📌 总结
- 回溯题里
path本质就是“递归路径的存储容器”,用ArrayList或LinkedList都可以。 - 如果要频繁访问下标(比如看最后一个元素),
ArrayList更好。 - 如果主要是在末尾加/删,
LinkedList更顺手(removeLast()很好用)。
47.全排列 II
本题 就是我们讲过的 40.组合总和II 去重逻辑 和 46.全排列 的结合,可以先自己做一下,然后重点看一下 文章中 我讲的拓展内容: used[i - 1] == true 也行,used[i - 1] == false 也行
https://programmercarl.com/0047.全排列II.html
视频讲解:https://www.bilibili.com/video/BV1R84y1i7Tm
全排列 I 的数组不包含重复数字,而II包含。因此涉及去重。
注意:去重一定要对元素进行排序,那样才方便通过相邻的节点来判断是否重复使用了

一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果。
class Solution {//存放结果List<List<Integer>> result = new ArrayList<>();//暂存结果List<Integer> path = new ArrayList<>();public List<List<Integer>> permuteUnique(int[] nums) {boolean[] used = new boolean[nums.length];Arrays.fill(used, false);Arrays.sort(nums);backTrack(nums, used);return result;}private void backTrack(int[] nums, boolean[] used) {if (path.size() == nums.length) {result.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {// used[i - 1] == true,说明同⼀树⽀nums[i - 1]使⽤过// used[i - 1] == false,说明同⼀树层nums[i - 1]使⽤过// 如果同⼀树层nums[i - 1]使⽤过则直接跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}//如果同⼀树⽀nums[i]没使⽤过开始处理if (used[i] == false) {used[i] = true;//标记同⼀树⽀nums[i]使⽤过,防止同一树枝重复使用path.add(nums[i]);backTrack(nums, used);path.remove(path.size() - 1);//回溯,说明同⼀树层nums[i]使⽤过,防止下一树层重复used[i] = false;//回溯}}}
}
理解:
由于是全排列,index=2的元素开始的数组也可以往回选index=1的元素作为其下个元素,因此每次for循环从i=0开始。
辨别是否选过该元素------>used 一条路径,指的是从root到leaf;这是递归不断深入的过程,used中不断有位置标记为true
防止选出相同的路径:排序+跳过同一层相邻相同的元素。当used[i-1]==false,这就意味着是回溯回来的同一树层的过程。
下面这三道题都非常难,建议大家一刷的时候 可以适当选择跳过。
因为 一刷 也不求大家能把这么难的问题解决,大家目前能了解一下题目的要求,了解一下解题思路,不求能直接写出代码,先大概熟悉一下这些题,二刷的时候,随着对回溯算法的深入理解,再去解决如下三题。
332.重新安排行程(建议跳过,力扣修改后台数据,应该不能用回溯了)
本题没有录制视频,当初录视频是按照 《代码随想录》出版的目录来的,当时没有这道题所以就没有录制。
https://programmercarl.com/0332.重新安排行程.html
51.N皇后(适当跳过)
N皇后这道题目还是很经典的,一刷的录友们建议看看视频了解了解大体思路 就可以 (如果没时间本次就直接跳过) ,先有个印象,二刷的时候重点解决。
https://programmercarl.com/0051.N皇后.html
视频讲解:https://www.bilibili.com/video/BV1Rd4y1c7Bq
37.解数独(适当跳过)
同样,一刷的录友们建议看看视频了解了解大体思路(如果没时间本次就直接跳过),先有个印象,二刷的时候重点解决。
。
https://programmercarl.com/0037.解数独.html
视频讲解:https://www.bilibili.com/video/BV1TW4y1471V
总结
刷了这么多回溯算法的题目,可以做一做总结了!
https://programmercarl.com/回溯总结.html