洛谷P3225 矿场搭建
据说点双连通分量的题少,而矿场搭建就是其中的一道好题,老师简单讲了一下我也是套板子AC了
题面具体点链接看,大概就是要求在无向图上修最少的救援点使得任意一个点坍塌了之后,剩下的点都能走走到一个救援点;
看到点断我也是第一时间想到割点,因为显然如果坍塌的点是一个割点,就能把图分成几个点双连通分量,这时需要的救援点显然是最多的;
想到这里我就直接套了点双连通分量的板子,每一个连通分量修一个救援点,方案数则是每个连通分量结点数的乘积,写完一测,哎呀样例都过不了好尴尬;
然后老师指点了一下才知道是要根据每个连通分量中的割点数不同来分不同情况讨论(其实应该自己多画几个图的,应该能自己想出来的);
其实这个性质是很明显的,比如考虑下面这个图:
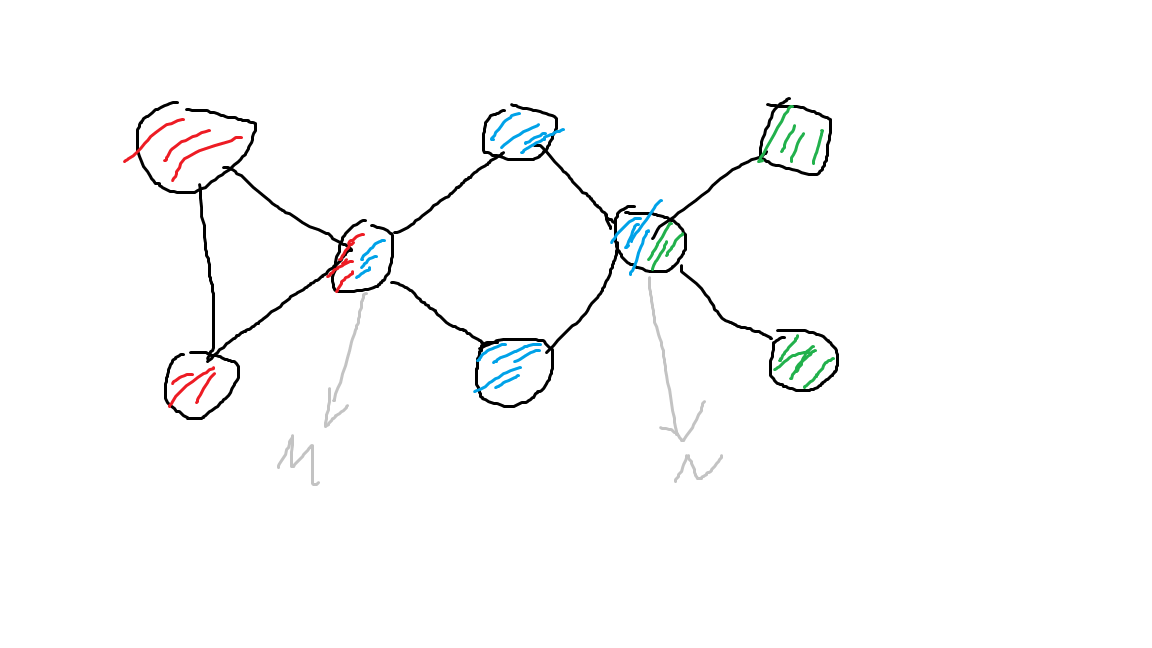
如图所示,红,蓝,绿三个部分分别是三个点双连通分量,M,N是两个割点;
现在我们注意蓝色部分的这个连通分量,显然无论是M点坍塌还是N点坍塌,蓝色点都能通过另外一个割点跑到另外一个连通分量去,所以它是不用建救援点的;更形式化的说:当一个连通分量中有两个及以上割点时,这个连通分量是不用建救援点的,它对答案没有任何贡献;
那么对于红色和绿色部分呢?它们只有一个割点,如果刚好是这个割点坍塌了红色点就将无处可去,所以必须在其中设置
一个救援点才行;能在哪些点设置呢?显然除了割点的点都可以;也就是说:当一个有n个结点的连通分量中只有一个割点时,救援点数会增加一个,且有n-1种设置方法(除去那个割点都可以设置)
最后我们还要考虑一种割点数为零的情况,显然这种情况是要建的,毕竟它没有割点,也就是说不能到其他连通分量的救援点去;那么建多少个呢?一个明显是不够的,万一刚好这个点坍塌呢?所以要建两个,而且可以任意选两个点建;也就是说:对于有n个结点且没有割点的连通分量,要建2个救援点,且有\(n\times(n-1)\div2\)种方案)(组合数化简可得)
另外要注意方案数要相乘(乘法原理)
以下就是ac代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 505;
int n, S, t, cnt, tot, ans, maxn, dfn[N], low[N], g[N]; //cnt记录dfs序,tot统计是第几组数据,maxn记录结点数
vector<int> mp[N], mp2[N];
vector<int> s; //用来维护的栈
void dfs(int u, int f){ //点双和割点的模板if(u == f && mp[u].empty()) { //特判孤点++ans;mp2[ans].push_back(u);return ;}dfn[u] = low[u] = ++cnt; //记录dfs序并初始化lows.push_back(u);for(auto v : mp[u]){if(v == f) continue;if(!dfn[v]){dfs(v, u);low[u] = min(low[u], low[v]);if(low[v] >= dfn[u]){ //如果是一个点双连通分量 ++ans;g[u]++; //u就是一个割点while(1){ //记录这个分量的点int x = s.back(); s.pop_back();mp2[ans].push_back(x);if(x == v) break; }mp2[ans].push_back(u); //把割点也放进去}}else low[u] = min(low[u], dfn[v]);}
}
signed main(){while(1){memset(dfn,0,sizeof(dfn));memset(low,0,sizeof(low));memset(g,0,sizeof(g)); ans = 0; cnt = 0; maxn = 0; //多测不清空,_______;tot++;cin >> n;if(n == 0) break;for(int i = 1; i <= n; i++){cin >> S >> t;if(S == t) continue;maxn=max(maxn, max(S, t)); //记录最大结点(题目不给)mp[S].push_back(t);mp[t].push_back(S);}for(int i = 1; i <= maxn; i++){if(dfn[i]) continue;dfs(i, i);g[i]--;}int ans1 = 0, ans2 = 1;for(int i = 1; i <= ans; i++){int num = 0;for(auto x : mp2[i]) if(g[x] > 0) num++; //统计割点数if(num >= 2) continue; //如果有两个及以上割点就不会对答案有贡献,直接跳过else if(num == 0){ //没有割点ans1 += 2; //新增两个救援点if(mp2[i].size() != 1) ans2 *= (mp2[i].size()*(mp2[i].size()-1))/2; //方案数}else if(num == 1){ //一个割点ans1 += 1; //救援点 + 1if(mp2[i].size() != 1) ans2 *= (mp2[i].size()-1); //可建在除割点外的任意一个点}} cout << "Case " << tot << ": " << ans1 << " " << ans2 << endl;for(int i = 1; i <= n; i++) mp[i].clear();for(int i = 1; i <= ans; i++) mp2[i].clear(); //清空}
}
