学习了统计学习方法的第一章
1.5正则化与交叉验证
(1)正则化的目的是模型选择的一个经典方法,正则化的是要使风险最小化的策略。正则化实在经验风险上加上一个正则化项,正则化项主要是防止模型在训练过程中出现过拟合的现象,一般正则项是由参数向量的L1,L2范式(注:L1是数据集中所有数据的绝对值的和/数据的个数,而L2是数据集中所有数据平方的和开根号/数据的个数)。
正则化为什么可以防止过拟合的数学解释

在公式中存在经验损失和正则化项,在选择模型的过程中一般选择经验损失最小的,而要选择最小的损失,我们需要对公式中的所有未知元素求偏导,是他们的偏导等于零从而来获得他们中的极小值,在极小值中进行比较就可以取得最小值.
而在进行上述操作的过程中,我们便可以将其与KKT及非线性规划最优解进行比较,发现正则化和带条件的优化是一致的,从而发现正则化对于模型选择的重要性。
(2)交叉验证便是对模型的检验,在选择好模型后,我们便需要对模型进行训练,测试和验证,这就需要我们将数据分为训练集,测试集和验证集,一般在数据充足的情况下,我们将依次将数据集分为90%,5%,5%给各个集。在验证方法上我们也分为简单验证方法,s折验证方法和留一验证方法。
简单验证方法就是将数据集分为两份,一份交给模型训练,一份交给验证
S折验证方法就是,将数据集分为S分只留一份验证,其余交给模型测试。如图
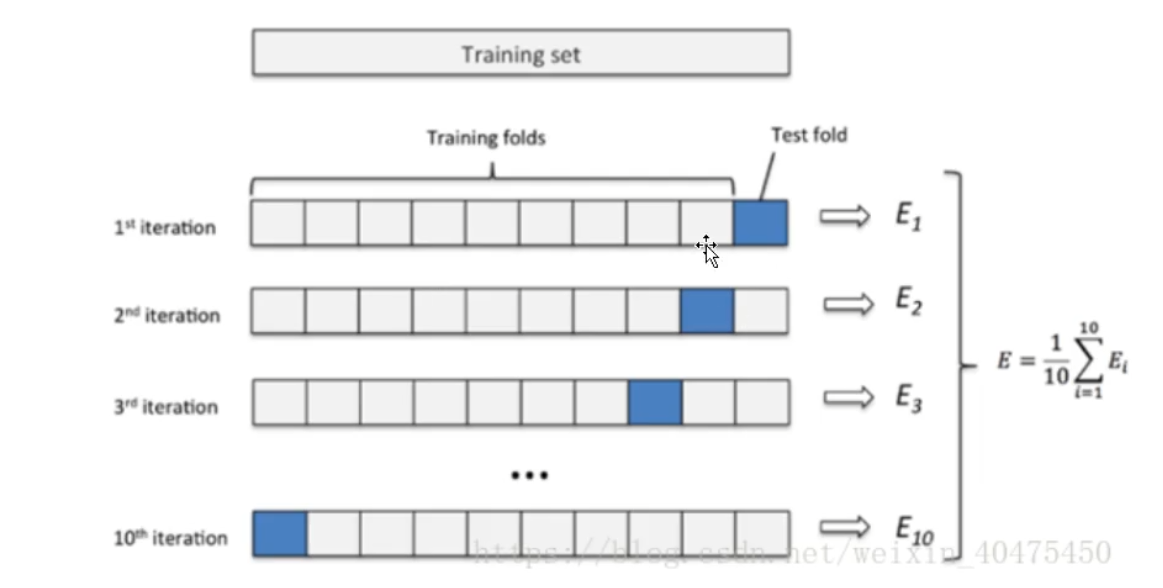
而留一是S折的特殊情况,每一份数据极为一折。
