Implicit Neural Representations with Periodic Activation Functions
SIREN:讨论sin激活函数在INR中的应用
代码仓库
注:本文涉及了一些笔者不了解的领域,仅摘取笔者自身比较熟悉的部分记录个人理解。
动机
利用sin激活函数帮助INR建模周期性且在导数上有一致性要求的信号。
方法
假设一种隐式神经表示的场景:将输入位置坐标\(x\)映射为某种感兴趣的信号,且监督导数:
本文方法SIREN使用MLP实现\(\Phi(\cdot)\),其中的每一层\(\phi_i(\cdot)\)都使用sin激活函数:
由于三角函数的导数性质,\(sin\)及\(cos\)的导数仍然是三角函数,因此SIREN的导数仍然继承了其自身的性质。因此,SIREN的任意阶导数也是若干SIREN的组合。
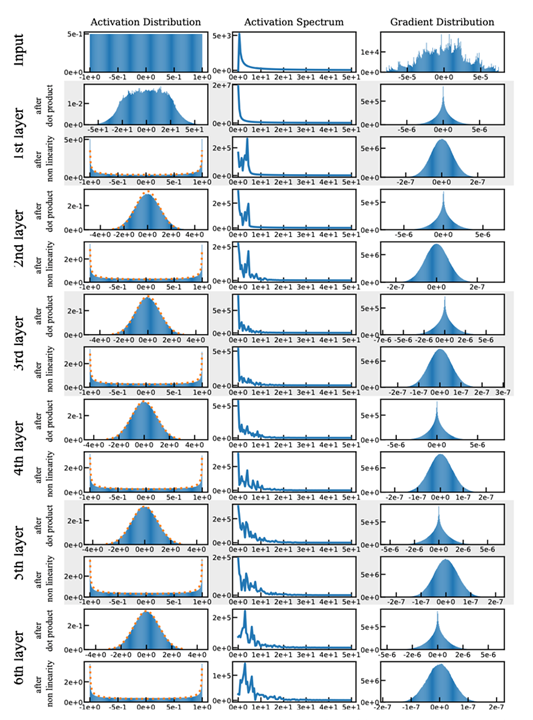
假设有一个简单的函数\(y=sin(ax+b)\),输入变量\(x\sim\mathcal{U}(-1,1)\),则对任意\(a>\frac{\pi}{2}\),有\(y\sim\arcsin(-1,1)\)。经过多层堆叠后接近正态分布,因此可根据这一性质设计权重初始化。
实验
图像重建

定义\(\mathbf{x}\)为图像上的坐标,目标为拟合对应位置上的RGB值\(f(\mathbf{x})\),监督RGB拟合的误差。实验中使用多种激活函数配置,并配以相当的网络。除了展示RGB结果外,还比较了梯度\(\nabla\Phi\)和拉普拉斯\(\Delta\Phi\)。可以看到SIREN拟合的结果和原图都相当一致。

该性质可以应用在泊松重构上:在一阶导上做图像融合得到的图像更平滑。
拟合周期性信号

由于三角函数天然具有周期性,所以适合用于拟合周期性信号,例如解决Helmholtz equation。
总结
本文主要讨论了sin作为激活函数在INR中的应用。其主要特点来源于三角函数的导数性质和周期性,也就因此能用于对导数和周期性有要求的任务。实现方法简单,效果明显。
