平面图
即所有边都不相交的图。
例:
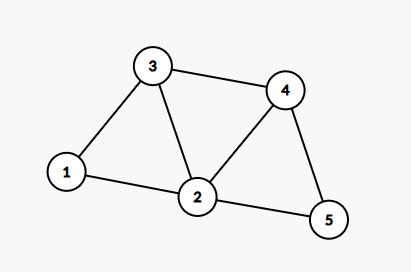
对偶图
将平面图中的面转为点,每条边连接其左右的两个面,一个朴素的例子:
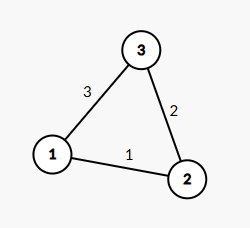
其对偶图为:
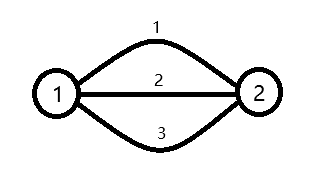
对偶图最短路
所以对偶图与最小割有什么关系呢?
在最小割问题中,我们经常会遇到面对平面图的最小割问题,但如果我们使用Dinic算法,\(O(n^2m)\) 的复杂度能让你当场AFO,此时就需要使用对偶图最短路了。
例:P2046 [NOI2010] 海拔
首先很显然,每个点的海拔高度只有可能是0或1,且肯定是左上部分是0,右下部分是1,显然是最小割。
但数据范围不支持我们用Dinic算法。
再进行观察,发现两端点海拔不同的边必然能形成一个路径,且路径两端不会同时位于左和下/右和上。
例:
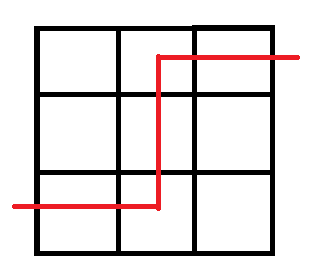
既如此,我们不妨将外部的面由左上到右下分割为二,对原来的每个边,我们令其顺时针旋转90度,代表从0走到1,即:
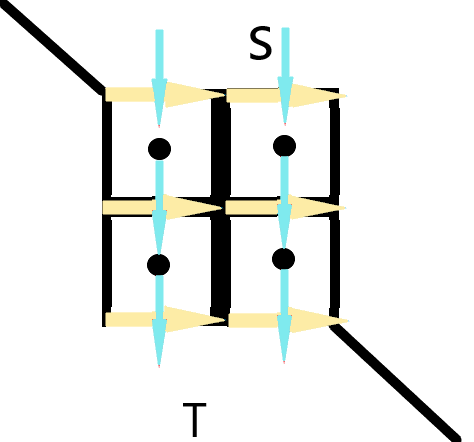
然后再跑一遍dijkstra就行啦。
