前言
彩笔运维勇闯机器学习:KNN算法,它也是分类中的一种
开始探索
scikit-learn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report, confusion_matrixnp.random.seed(0)x0 = np.random.randn(60, 2) * 0.6 + np.array([1, 2])
x1 = np.random.randn(30, 2) * 0.6 + np.array([3, 4])
x2 = np.random.randn(10, 2) * 0.6 + np.array([1, 5])X = np.vstack((x0, x1, x2))
y = np.array([0]*60 + [1]*30 + [2]*10)X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)scaler = StandardScaler()
X_train_std = scaler.fit_transform(X_train)
X_test_std = scaler.transform(X_test)k = 5
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train_std, y_train)
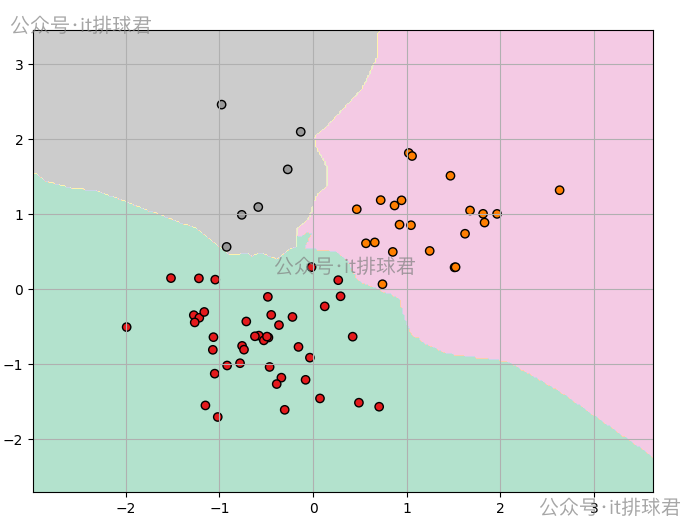
y_pred = knn.predict(X_test_std)def plot_knn_decision(X, y, model):h = 0.02x_min, x_max = X[:, 0].min()-1, X[:, 0].max()+1y_min, y_max = X[:, 1].min()-1, X[:, 1].max()+1xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))Z = model.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.figure(figsize=(8,6))plt.contourf(xx, yy, Z, cmap=plt.cm.Pastel2)plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.Set1)plt.grid(True)plt.show()plot_knn_decision(X_train_std, y_train, knn)这是一个三分类的数据,分类0有60个,分类1有30个,分类2有10个
脚本!启动:
深入理解KNN
KNN算法属于惰性学习,没有所谓的数据训练的过程。它把训练数据暂时保存,当有新的数据需要进行分类时,再使用训练数据进行对应的计算,而这个计算算法常见的是欧氏距离
下面用一个例子来加深一下算法的过程
举例说明
假设有以下训练数据
| x1 | x2 | 类别 | |
|---|---|---|---|
| A | 1 | 2 | 0 |
| B | 2 | 3 | 0 |
| C | 3 | 3 | 1 |
| D | 6 | 5 | 1 |
| E | 7 | 2 | 1 |
1)由于是惰性学习,训练数据就先放着备用
2)假设有一个测试数据,T(3,4),需要对他进行分类
对每一个点分别计算:
- A点,(1,2),\(D_A=\sqrt{(3-1)^2+(4-2)^2} \approx 2.83\)
- B点,(2,3),\(D_A=\sqrt{(3-2)^2+(4-3)^2} \approx 1.41\)
- C点,(3,3),\(D_A=\sqrt{(3-3)^2+(4-3)^2} = 1\)
- D点,(6,5),\(D_A=\sqrt{(3-6)^2+(4-5)^2} \approx 3.16\)
- E点,(7,8),\(D_A=\sqrt{(3-7)^2+(4-8)^2} \approx 5.66\)
3)设置超参数K=3,选择3个距离最小作为邻居
| 邻居 | 距离 | 类别 |
|---|---|---|
| C | 1 | 1 |
| B | 1.41 | 0 |
| A | 2.83 | 0 |
4)投票,少数服从多数,T(3,4)的类别是0
小结
KNN算法的优点是简单直接,非常容易理解。缺点也很明显,由于是惰性计算,面对高维的、数据量非常大的数据,往往需要大量的计算才能进行分类,并且对于每一个测试数据都需要“遍历所有训练数据”来计算距离,这在大规模 数据集上会变得非常慢。
异常检测
在之前讨论分类问题的时候,遇到了所谓的“类别不平衡”问题,就是多数类占据样本的大量,而少数类只占用非常少的样本,导致分类算法对于少数类不能正确分类,需要做额外的处理
在实际工作中,“类别不平衡”问题有着非常重要的实践,比如有100w的日志,怎么精准识别出10条异常日志,除了10条日常,其余999990条日志都属于正常日志。对于这种问题又叫做“异常检测”,对于“异常检测”问题,有一些算法是比较擅长处理的,比如KNN算法
举例说明
在下列数据中,找出异常点
| x1 | x2 | |
|---|---|---|
| A | 1 | 2 |
| B | 2 | 3 |
| C | 3 | 3 |
| D | 6 | 5 |
| E | 7 | 2 |
1)算法没变,还是使用欧式距离公式
| A(1,2) | B(2,3) | C(3,3) | D(6,5) | E(7,8) | |
|---|---|---|---|---|---|
| A(1,2) | - | 1.41 | 2.83 | 5.83 | 8.49 |
| B(2,3) | 1.41 | - | 1 | 4.24 | 6.71 |
| C(3,3) | 2.83 | 1 | - | 3.61 | 5.83 |
| D(6,5) | 5.83 | 4.24 | 3.61 | - | 3.16 |
| E(7,8) | 8.49 | 6.71 | 5.83 | 3.16 | - |
2)设置超参数K=2,找到最近的2个邻居计算平均距离
- A最近的邻居:(1.41 2.83),\(D_A=2.12\)
- B最近的邻居:(1 1.41),\(D_B=1.21\)
- C最近的邻居:(1 2.83),\(D_C=1.91\)
- D最近的邻居:(3.16 3.61),\(D_D=3.39\)
- E最近的邻居:(3.16 5.83),\(D_E=4.5\)
3)找出异常点
- 如果要找出最异常的,那就是E点
- 如果要找出2个的异常点,那就是D与E
scikit-learn
import numpy as np
from sklearn.neighbors import NearestNeighborsnp.random.seed(42)
X_normal = np.random.randn(100, 2)
X_outliers = np.array([[5, 5], [-5, -5], [6, -6]])
X = np.vstack((X_normal, X_outliers))k = 3
nbrs = NearestNeighbors(n_neighbors=k)
nbrs.fit(X)
distances, _ = nbrs.kneighbors(X)
k_dist = distances[:, -1]n_outliers = 3
threshold = np.partition(k_dist, -n_outliers)[-n_outliers]
outlier_mask = k_dist >= thresholdoutliers = X[outlier_mask]
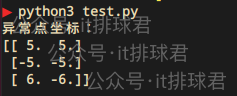
print("异常点坐标:")
print(outliers)脚本!启动:
画图分析
import matplotlib.pyplot as pltplt.figure(figsize=(8,6))
plt.scatter(X[:, 0], X[:, 1], c='blue')
plt.scatter(outliers[:, 0], outliers[:, 1], c='red', edgecolors='black', s=100)
plt.legend()
plt.grid(True)
plt.show()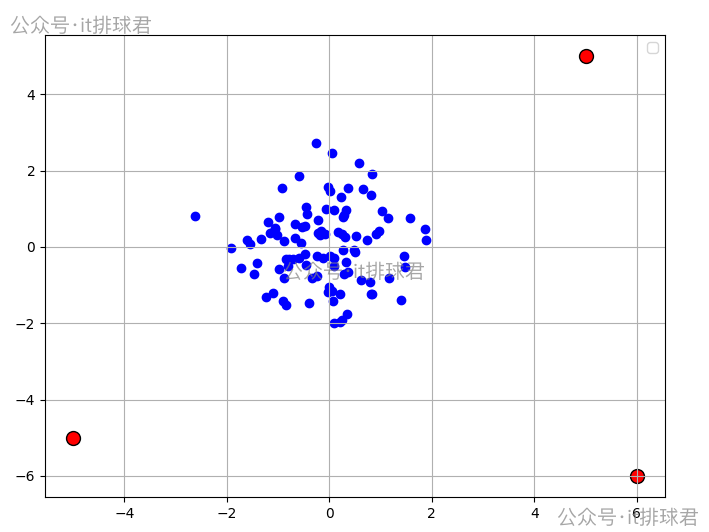
KNN增强版本LOF
局部离群因子(LOF)算法,专门用于异常检测
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactorX = np.array([[1, 2],[2, 3],[3, 3],[6, 5],[7, 9],[20, 20],
])k = 2
lof = LocalOutlierFactor(n_neighbors=k, contamination=0.3)
y_pred = lof.fit_predict(X)anomaly_scores = lof.negative_outlier_factor_
for i, (point, label, score) in enumerate(zip(X, y_pred, anomaly_scores)):status = "异常" if label == -1 else "正常"print(f"点 {i}: 坐标={point}, 状态={status}, LOF分数={score:.3f}")n_neighbors=2,就是超参数k,用来选择邻居数contamination=0.3,表示有30%的数据为异常
脚本!启动:
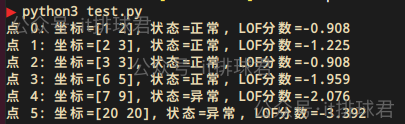
两种算法的对比
| KNN | LOF | |
|---|---|---|
| 功能 | 查找最近邻居 | 检测局部异常 |
| 输出 | 每个点最近的 k 个邻居及其距离 | 每个点的异常标签(1 或 -1)和 LOF 分数 |
| 适用任务 | 查找最近的用户/商品/样本 | 检测数据中的异常点 |
| 是否计算异常 | 否 | 是(negative_outlier_factor_) |
| 参数 | n_neighbors 只是最近邻个数 | n_neighbors, contamination 控制邻居数和异常比例 |
小结
- 联系我,做深入的交流
![]()
至此,本文结束
在下才疏学浅,有撒汤漏水的,请各位不吝赐教...

