Part 1 题目列表
- P7075 [CSP - S2020] 儒略日
- P7076 [CSP - S2020] 动物园
- P7077 [CSP - S2020] 函数调用
- P7078 [CSP - S2020] 贪吃蛇
Part 2 考试时间线
8:02 开题, 仅仅读了 10 分钟 T1 题目,就得出结论,大模拟。
9:20 在与 T1 长达 ···(数不过来了) 的搏斗后,成功过了大样例,快速开 T2。
9:50 十分钟看题,十分钟写题,十分钟调题(算多了一点),一遍过大样例。
11:00 当时一看,这不明显的数据结构大水题吗(看看我那惊人的判断力),最终没调出来。
11:20 只好写了一个超级大暴力。但当我把视野望向那仿佛遥不可及的 T4 时,却发现这不是 贪吃蛇 吗,我以前可是做过的,但是没调出来。
12:00 结束,开始担心未删调试。
Part 3 题目分析
T1
都说了是 超级打分讨,当然要加一点二分。
错因:
有一个 1582 写成了 1982
T2
最简单的一道,就不再多说了,要注意的是,答案最大值为:
开 unsigned long long 都会爆。
所以要特判。
T3
考完后成功发现时间复杂度是伪的。
首先这怎么看都像是一个图论,因为通过函数的调用关系,可以很轻松的建立一个 DAG 出来
比如这组数据:
【输入】
1
0
5
1 1 1
2 2
2 4
3 2 1 2
3 2 1 3
2
4 5
【输出】
12
可以建出如下图:
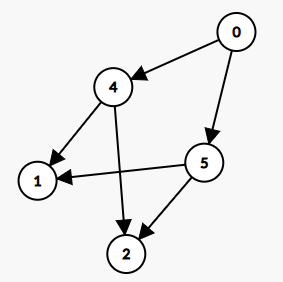
这里补了一个 0 号节点作为主函数,相当于只是调用一个主函数
首先我们发现:
所以我们只需要分别知道原数组乘的倍数,和每一个加数乘的倍数即可。
第一个十分简单,一个反向建边,加一个拓扑即可。
而第二个有一点需要注意,我们要反向枚举边,因为是后面的影响前面的。
T4
这里做一个分类讨论:
-
最大的蛇吃了最小的蛇不是最小的蛇
【策略】
应当吃掉,如何都不亏(证明略)
-
最大的蛇吃了最小的蛇是最小的蛇
【策略】
最开始我们头脑简单的认为这当然不能吃,因为吃了自己下一轮也得死,但是当我们再往下面枚举一层:
-
下一轮最大的蛇吃了自己不是最小的蛇
因为这条蛇会选择吃你,因而你在这一轮不能吃
-
下一轮最大的蛇吃了自己是最小的蛇
这里又要看下下一轮的蛇
-
我们发现这是一个递归的过程,一但要考虑第二种情况就会递归到:
- 蛇的数量为 2
- 这条递归到的蛇吃了后不是最小的蛇
且满足:
- 上个蛇要吃则这一个蛇不吃
- 上一个蛇不吃则这一个蛇吃
(满足奇偶性)
Part 4 总结
| 题目 | 预估分数 | 实际得分 | 核心算法 | 错因 | 改进方案 |
|---|---|---|---|---|---|
| 儒略日 | 100 | 70 | 模拟+分类讨论+二分 | 1582写成了1982(luogu上出现了一些TLE,但LemonLime没有) | 在检查时检查一些特殊情况(边界,如这道题的1582年) |
| 动物园 | 100 | 95 | 位运算 | 未考虑 ans=(1<<64) 的情况 | 检查特殊情况,查看是否越界 |
| 函数调用 | 45 | 45 | DAG拓扑+思维 | 方法选错了,且特殊性质没调出来 | 当发现不能在短时间内找到正解的话,先保证打满部分分 |
| 贪吃蛇 | 20 | 20 | 贪心+优先队列 | 时间不够,只能打完20分 | 节约时间 |
总分:70 + 95 + 45 + 20 = 230
预期得分: 100+100+45+20=265
改进方案:
- 在检查时检查一些特殊情况
- 当发现不能在短时间内找到正解的话,先保证打满部分分
- 节约时间
