此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第一课第三周,3.11部分的笔记内容,同时也是本周理论部分的最后一篇。
经过第二周的基础补充,本周内容的理解难度可以说有了很大的降低,主要是从逻辑回归扩展到浅层神经网络,讲解相关内容,我们按部就班梳理课程内容即可,当然,依旧会尽可能地创造一个较为丝滑的理解过程。
上一篇通过展开讲述激活函数的作用,并再次过了一遍浅层神经网络的传播过程,来说明浅层神经网络如何提高拟合能力,本篇则补上最后一块拼图,同时也是本周理论部分的最后一篇。
在这周的例子里,我们设置神经网络隐藏层的神经元为四个,输出层的神经元再综合四个神经元的输出结果计算最终的输出,那隐藏层神经元的数量增加后,又是如何发挥正向的作用呢?
我们知道每个神经元都有自己的参数,我们通过不断训练参数达到拟合效果,如何让每个神经元都真的对拟合起到帮助作用,就是本篇的内容:随机初始化
1. 什么是初始化
在训练神经网络之前,我们并不知道哪些参数(权重 \(W\) 和偏置 \(b\))是最好的,因此需要先给它们一个“起始值”,这个过程就叫做初始化。
这些初始值相当于我们在参数空间中的“出发点”,之后通过梯度下降不断调整,逐步逼近损失函数的最小值。
简单来说,就是赋初值。
2. 为什么要随机初始化
在逻辑回归中,我们并不强调初始化内容,这是因为整个网络只有一层线性组合与其相关的参数,我们的所有操作都是在更新这一组参数,因此,把这组参数初始化成什么样,并不算一个需要思考的地方,因为这组参数最终都会随着更新到底损失的最低点。
而现在,我们在隐藏层设置四个神经元,如果所有参数一开始都设为同一个值(例如全为 0),会出现一个非常严重的问题,我们看这样一个过程:
- 每个隐藏层神经元收到的输入一样;
- 计算得到的中间结果也完全一样;
- 反向传播时梯度也一样;
- 于是所有神经元更新后的参数依旧完全相同;
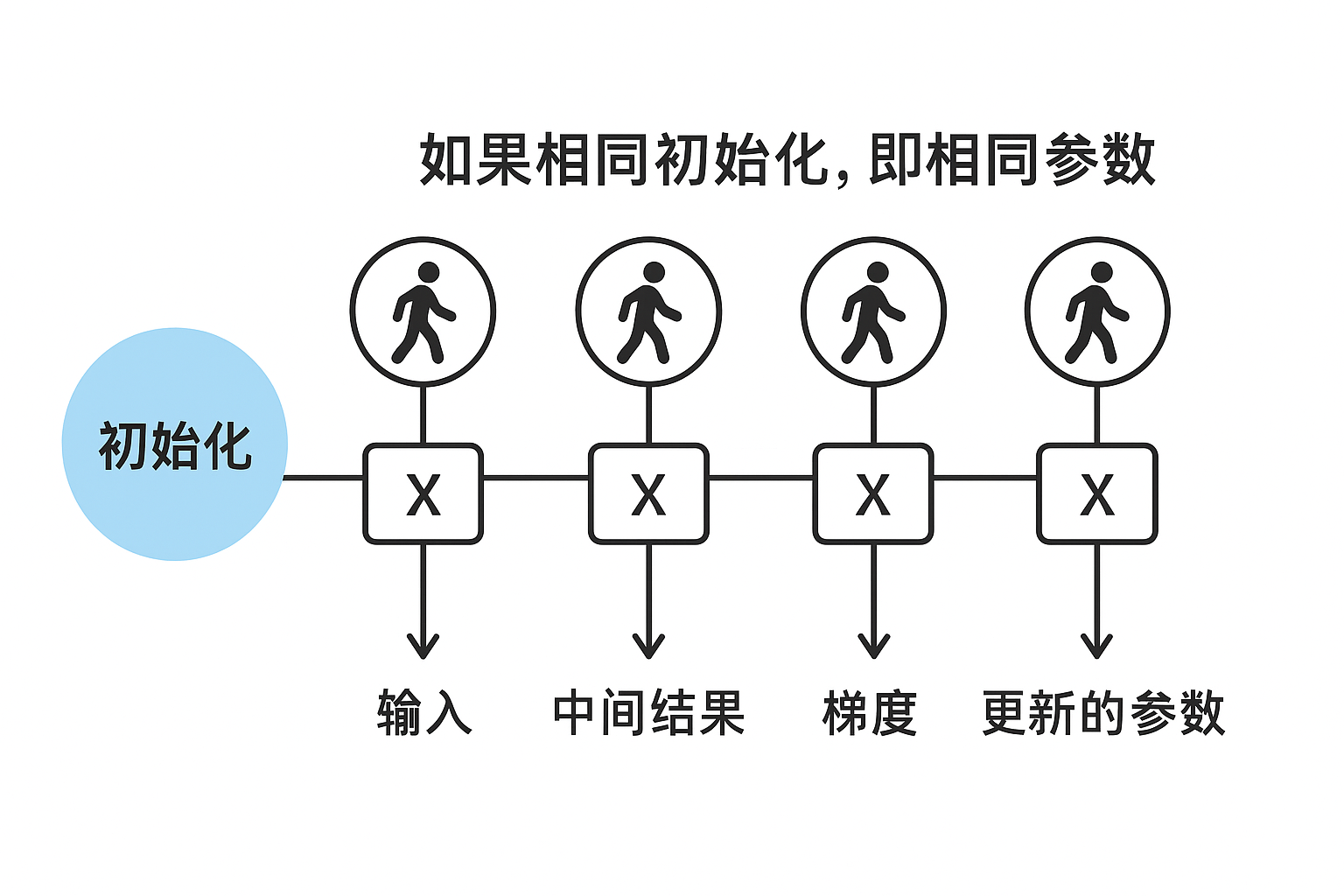
这样训练下去,即使我们设置了很多神经元,它们都在“做同样的事情”,模型就退化成只有一个神经元的效果。用专业术语来说,这叫对称性问题(Symmetry Problem)。
而解决办法就是在初始化时给每个神经元赋予一个不同的随机初始权重,打破对称性,让它们在训练过程中各自朝不同方向学习。
3.损失的凸与非凸问题
我们说逻辑回归不存在对称性问题,还有另外一个关键原因:它的损失函数是凸函数。
在第二周第四部分我们讲过,凸函数具有一个非常重要的特性:全局范围内只有一个最低点(全局最小值)。
这意味着:无论参数从哪里初始化, 只要我们沿着梯度下降方向不断更新参数,最终都会收敛到同一个最优点。
因此即使初始化相同,甚至初始化为 0,也不会导致模型陷入“学不动”或者“神经元行为完全一样”的问题,如下图所示:
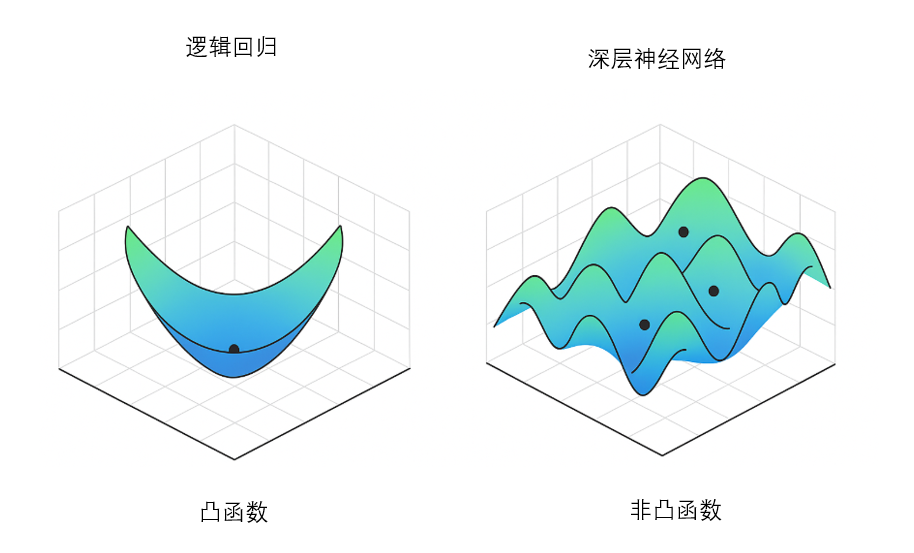
但当我们从逻辑回归(单一线性变换)扩展为神经网络(包含隐藏层、激活函数、多个权重矩阵)时,经过无数函数的相乘,损失函数就不再是一个光滑的碗形函数,而变成了一个复杂的山地地形。
有无数个山峰(局部最大值)、山谷(局部最小值)、鞍点(既不是峰也不是谷)。
此时,损失函数不是凸函数,而是非凸的。
因此,我们才需要随机初始化不同的神经元,来不断探索损失函数的最小值。
4.举例类比随机初始化的作用
我们依旧用山坡来举例:
现在,我们派 4 个登山者去寻找一片山地的最低点(损失函数的最小值):
| 情况 | 结果 |
|---|---|
| 所有人从同一个山顶出发(全零初始化) | 大家看到的坡度一样,朝同一个方向走,走的路径重叠,只等于一个人找路,效率极低。 |
| 每个人从不同位置出发(随机初始化) | 各自看到的坡度不一样,探索方向不同,更可能有人找到更低的谷底(更优解)。 |
因此,随机初始化就是给每个神经元一个不同的出发点,让它们探索不同的优化空间。
5. 权重的随机初始化
在神经网络中,隐藏层的每个神经元都拥有属于自己的权重参数 \(W\) 和偏置 \(b\)。
如果我们把所有权重都初始化为相同的值,就会造成一个严重的问题:对称性永远无法被打破,所有神经元的行为完全一样,网络就失去了“多神经元协作学习”的意义。
因此,我们需要为每一个权重赋予一个随机的初始值,这就叫做权重随机初始化。
它并不是让权重变得“乱七八糟”,而是把它们设定在一个很小且随机的范围内,例如:
这样,就可以打破对称性,实现多个隐藏神经元探索多个不同方向的效果。
而对于权重的随机初始化,也有一些科学的初始化算法,我们遇到再说。
6. 偏置的初始化
与权重不同,偏置 \(b\) 一般不需要随机初始化,而是直接初始化为 0 或一个很小的常数。
这是因为偏置项不会造成之前提到的“对称性问题”,它作为一个常数,只是简单地把激活函数的输入整体向左或向右平移,不会影响神经元之间是否相同。
因此,在权重已经随机初始化实现了打乱效果后,我们便不会把过多的算法性能浪费在偏置上。
总结
这便是本周课程的最后一部分内容,相比第二周需要较多的基础补充,本周其实只是实现了从逻辑回归到浅层神经网络的扩展,了解了神经网络规模增加是如何帮助拟合的。
下一篇的内容便是本周的课后习题和代码实践,我们用实操来感受一下带隐藏层的神经网络相比逻辑回归带来的性能提升。
