花了三篇文章的时间大致讲了讲我对于rfsoc时钟树的理解,非常的浅薄与浅应用,现在我再从原理层面记录一下我对于rf data converter这个ip核里面三种混频模式从底层上的了解,这一篇主要记录一下带通采样定理的知识,下一篇会涉及到三种混频模式的配置不同
在这里采样和频谱混叠等本科基础知识就不再赘述,直奔主题
带通采样定理
我们在大学课堂里学习的奈奎斯特采样定理内容一般都是采样率必须大于你要采集的信号的最高频率的两倍,才能避免频谱混叠
但在很多射频或通信系统中,信号不是从 0 开始的低频信号,而是高频载波附近的窄带信号,例如:一个中心在 1 GHz、带宽只有 20 MHz 的信号,或者一个经过上变频的 IF(中频)信号,范围在600-650MHz,这时候如果我们仍然用最基础的采样定理去采样,那就要使用大于等于2GHz左右的采样率,非常浪费,为什么会浪费?因为我们只关心那个窄带里面的信息,我们不需要高频的载波,于是我们就需要带通采样定理,也叫欠采样定理
带通采样定理要求我们在采样频率低于低通采样频率的时候也能无失真地还原信号,他允许混叠,但是要求混叠恰好落在我们想要的频率位置,在各频带不重叠的同时,混叠后的频谱可以唯一还原
数学形式
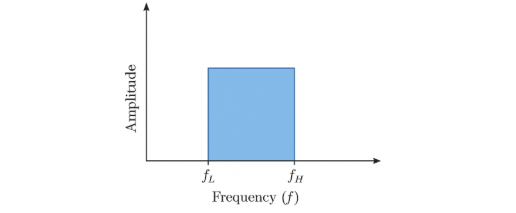
假设信号的频谱位于
则为带通信号,带宽
对于采样而言,采样会把信号的频谱“周期复制并镜像”,对连续信号 x(t)以采样频率fs 采样,得到的频谱(正频部分)是原谱的按间隔fs 复制,同时在每个周期区间有折叠现象
所以在频轴上会出现一列“原谱副本”,中心分别位于 …,−2fs, −fs, 0, fs, 2fs,…;对于实信号还要考虑镜像对称
我们希望经过采样后,[fL,fH]被映射到数字域的某一段(例如落入 [0, fs/2]),并且不同副本之间不发生重叠,换句话说,我们需要存在一个整数 n 使得原带恰好位于两个相邻的“镜像边界”之间:
以为单位,正频率轴上的边界序列
这些值是发生折叠的边界,所以我们需要存在一个整数大于等于1的整数n,使得原来的带通信号那个带通的带完整的落入区间
也就是说
且
解这个不等式就可以轻松得到
通过这个不等式我们就可以找到满足一个区间里都可以的采样率
举例
假如fL=700 MHz,fH=720 MHz,则带宽 B=20 MHz
我们在计算的时候可以通过凑数字来找到合适的采样率,例如我们发现在n=4的时候,
所以我们就可以选择400MHz作为带通信号的采样率,实现了低采样率采高频信号
奈奎斯特区
在低通采样定理中,就是奈奎斯特采样率,在这个情况下信号位于第一奈奎斯特区,由此引出定义,
当采样频率 fs 固定后,我们可以把频谱分成一系列带宽为一半采样率的区域:
第1奈奎斯特区: [0,fs/2],第2奈奎斯特区: [fs/2,fs] 第3奈奎斯特区: [fs,3fs/2] 第n奈奎斯特区: [(n−1)fs/2,nfs/2]
每一个这样的带宽区间称为一个奈奎斯特区,由于采样后频谱是以 fs 为周期周期性展开的,这些区会折叠叠加到 基带区 内(即 0~fs/2),所以在带通采样的过程中,上述公式里的n也就是第n奈奎斯特区,利用这个频谱折叠的规律,就可以把信号恰好折叠到第一奈奎斯特区
但是这里要注意一点,如果n是奇数,则折叠之后频谱不反相,若n是偶数,则折叠之后频谱反相
下一篇会讲解一下具体设置混频的原理以及设置