克鲁斯卡尔(Kruskal)算法从另一途径求网的最小生成树。其基本思想是:假设连通网G=(V,E),令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{}),概述图中每个顶点自成一个连通分量。在E中选择代价最小的边,若该边依附的顶点分别在T中不同的连通分量上,则将此边加入到T中;否则,舍去此边而选择下一条代价最小的边。依此类推,直至T中所有顶点构成一个连通分量为止。——百度百科
比较抽象,\(kruskal\)算法利用直接存边的方法存图,对存储的边进行升序排序,从小到大加入我们的最小生成树中,并且结合并查集来检查是否会生成环,如果会生成环,那么我们就不把它加入到我们的最小生成树中,反之加入。
还是有点抽象,我们结合图来理解一下整个过程。
本代码根据洛谷P3366 【模板】最小生成树所写。传送锚点
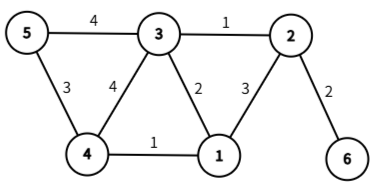
此时,我们程序已经输入完成,并已经将边升序排序。

按照升序排序,我们应将最小的边先加入最小生成树中,显然,此时没有环生成,所以我们这两条边都可以添加。
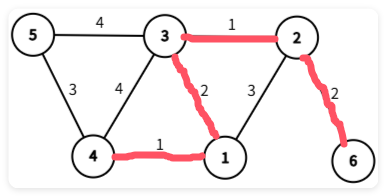
现在我们要加入第二小的边,也没有环出现,可以添加。
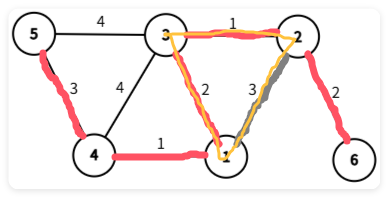
现在我们要加入第三小的边,显然,有一条边(灰色标注)与当前的树生成了环(黄色标注),所以我们不能将这条边加入到我们的最小生成树中。
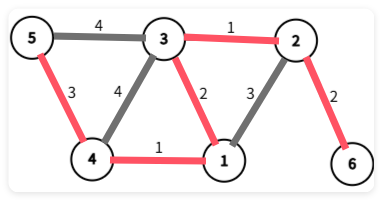
(画到这突然发现有能画直线的工具qwq)两条\(weight=4\)的边加入也会生成边,所以我们都不加入。
所以我们此图的最小生成树就有了:
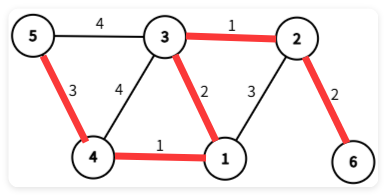
具体实现:
道理都懂了,代码如何实现呢(此处参考了这篇博客的写法)
首先,我们要直接存边,当然你可以分开存(可能会有点麻烦),这里我们使用一个结构体来保存每一条边的信息:
struct EDGE{ll w;ll pre, to;
} tree[maxn];
\(w\)为当前边的权值,\(pre\)是这条边的起始点,\(to\)是这条边的终点。
问题来了,我们如何用并查集判断当前边加入后是否会生成环呢?
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。——百度百科
(不会并查集可以先去学一下)使用并查集,用\(f\)数组存每个点的父亲,我们可以将每条边起点的父亲设为终点f[find(tree[x].pre)] = find(tree[x].to);,这样,我们就将插入的这条边的起点终点都并入到了并查集中。
那么怎么判断呢?如果我们这条边的起点终点的祖先是同一个find(tree[i].pre) == find(tree[i].to),那么说明生成了环。

(红色代表已经加入并查集)例如这种情况,现在我们要加入\(5\)到\(0\)这条边,这两个点既然已经加入了并查集,所以它们俩的祖先是相同的,显然符合find(tree[i].pre) == find(tree[i].to)这种情况,我们就直接跳过。
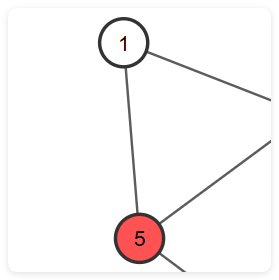
另一种情况,我们要加入\(5\)到\(1\)这条边,\(5\)在并查集中,\(1\)不在并查集中,这俩显然没有相同祖先,可以加入。
剩下一种俩点都不在并查集内的情况就不再赘述了。
void build(ll x){ans += tree[x].w; //答案加上权值f[find(tree[x].pre)] = find(tree[x].to); //将起点终点连接(加入并查集)return ;
}
ll find(ll x){ //查找祖先return f[x] == x ? x : f[x] = find(f[x]); //路径压缩写法,会更快
}
for (ll i = 1;i <= m;i ++) {if (num == n - 1) break; //最小生成树的边数很显然是点数-1(没有环,两两相连),边数到了就没有必要继续了if (find(tree[i].pre) == find(tree[i].to)) continue;//如果会生成环,就不添加此边build(i); ++ num;//边数加1}
完整代码:
#include <iostream>
#include <algorithm>
using namespace std;
const ll maxn = 2e5 + 5;
struct EDGE{ll w;ll pre, to;
} tree[maxn];
ll ans, f[maxn], num=0;
bool cmp(EDGE a, EDGE b){return a.w < b.w;
}
ll find(ll x){return f[x] == x ? x : f[x] = find(f[x]);
}
void build(ll x){ans += tree[x].w;f[find(tree[x].pre)] = find(tree[x].to);return ;
}
ll main(){ll n, m, x, y, z;cin >> n >> m;for (ll i = 1;i <= m;i ++) {cin >> x >> y >> z;tree[i].pre = x;tree[i].to = y;tree[i].w = z;}sort(tree + 1, tree + m + 1, cmp);for (ll i = 1;i <= n;i ++)f[i] = i;for (ll i = 1;i <= m;i ++) {if (num == n - 1) break;if (find(tree[i].pre) == find(tree[i].to)) continue;build(i); ++ num;}if (num != n - 1){cout << "orz";return 0;}cout << ans;return 0;
}
可\(AC\)通过洛谷P3366 【模板】最小生成树传送锚点
下面我们来看一道简单的例题:
洛谷P1195 口袋的天空传送锚点

读题发现,这道题要连成\(K\)个棉花糖,而且要让花费的代价最小,其实就是我们的最小生成树。
其实就是把图中的点用一颗最小生成树连接起来,但是最后的答案要去掉其中的几条边,使这棵树变成\(K\)块。
完整跑完一遍\(kruskal\)然后再去掉其中最大的几条边比较麻烦,还需要记录这棵树中存在的每一条边,然后从大往小删除(不能从图中的所有边里面从大往小删,根据我们上面的例子,图中最大的边是4,但是两条权值为4的边都不在树中,所以会出现错误,所以想要这样做必须要记录树中的边)
我们可以从另外一种角度想一想,我们想要分成\(K\)块,我们是不是需要删除\((K(块数)-1)\)条边啊,最小生成树里\(M(边数)=N(点数)-1\),所以我们最小生成树中总共有\(N-1-(K-1)=N-K\)条边,那么我们只需让\(kruskal\)在有\(N-K\)条边时停止,就能得到我们的最终答案。
代码:(可\(AC\)通过)
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 2e5 + 5;
struct EDGE{int w;int pre, to;
} len[maxn];
int ans, f[maxn], num=0, tw[maxn], tot=0;
bool cmp(EDGE a, EDGE b){return a.w < b.w;
}
int find(int x){return f[x] == x ? x : f[x] = find(f[x]);
}
void build(int x){ans += len[x].w;tw[tot ++] = len[x].w;f[find(len[x].pre)] = find(len[x].to);return ;
}
int main(){int n, m, T;cin >> n >> m >> T;if (T > n){cout << "No Answer";return 0;}for (int i = 1;i <= m;i ++) {int x, y, z;cin >> x >> y >> z;len[i].pre = x;len[i].to = y;len[i].w = z;}sort(len + 1, len + m + 1, cmp);for (int i = 1;i <= n;i ++) f[i] = i;for (int i = 1;i <= m;i ++) {if (num == n - T) break;if (find(len[i].pre) == find(len[i].to)) continue;build(i);++ num;}if (num != n - T){cout << "No Answer";return 0;}cout << ans;return 0;
}
