一、预备知识
1. 强连通图
有向图 \(G\) 强连通是指,\(G\) 中任意两个结点连通。
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图。
2. DFS 生成树
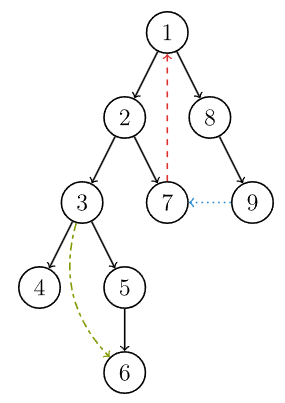
有向图的 DFS 生成树主要有 4 种边(不一定全部出现):
- 树边(tree edge):示意图中以黑色边表示,每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
- 反祖边(back edge):示意图中以红色边表示(即 \(7→1\)),也被叫做回边,即指向祖先结点的边。
- 横叉边(cross edge):示意图中以蓝色边表示(即 \(9→7\)),它主要是在搜索的时候遇到了一个已经访问过的结点,但是这个结点 并不是 当前结点的祖先。
- 前向边(forward edge):示意图中以绿色边表示(即 \(3→6\)),它是在搜索的时候遇到子树中的结点的时候形成的。
3. DFS 生成树和强连通分量的关系
如果结点 \(u\) 是某个强连通分量在搜索树中遇到的第一个结点,那么这个强连通分量的其余结点肯定是在搜索树中以 \(u\) 为根的子树中。结点 \(u\) 被称为这个强连通分量的根。
二、Tarjan 算法
1. 概述
Robert E. Tarjan(罗伯特·塔扬,1948~),生于美国加州波莫纳,计算机科学家。
Tarjan 发明了很多算法和数据结构。不少他发明的算法都以他的名字命名,以至于有时会让人混淆几种不同的算法。比如求各种连通分量的 Tarjan 算法,求 LCA(Lowest Common Ancestor,最近公共祖先)的 Tarjan 算法。并查集、Splay、Toptree 也是 Tarjan 发明的。
大牛啊。
2. 思路
Tarjan 算法基于对图进行深度优先搜索。
我们视每个连通分量为搜索树中的一棵子树,在搜索过程中,维护一个栈,每次把搜索树中尚未处理的节点加入栈中。
对于每一个 \(u\),维护这么几个变量:
- \(dfn_u\):深度优先搜索时 \(u\) 被搜索的次数,即 dfs 序中对应的编号;
- \(low_u\):在以 \(u\) 为根的子树中最早能遍历到的节点。
可以证明一个有趣的结论:在从根节点到一个叶子节点的路径上,\(dfn\) 严格单增,\(low\) 严格非降。
按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索,维护每个结点的 \(dfn\) 与 \(low\) 变量,且让搜索到的结点入栈。每当找到一个强连通元素,就按照该元素包含结点数目让栈中元素出栈。
对于节点 \(u\) 和节点 \(v\),\(v\) 不是 \(u\) 的父亲节点:
- \(v\) 未被访问:继续访问 \(v\),并用 \(low_v\) 来更新 \(low_u\);
- \(v\) 被访问过,已在栈中:用 \(dfs_v\) 跟新 \(low_u\);
- \(v\) 被访问过,不在栈中:无需处理。
把代码转换为伪代码:
TARJAN_SEARCH(int u)vis[u]=truelow[u]=dfn[u]=++dfncntpush u to the stackfor each (u,v) then doif v hasn't been searched thenTARJAN_SEARCH(v) // 搜索low[u]=min(low[u],low[v]) // 回溯else if v has been in the stack thenlow[u]=min(low[u],dfn[v])
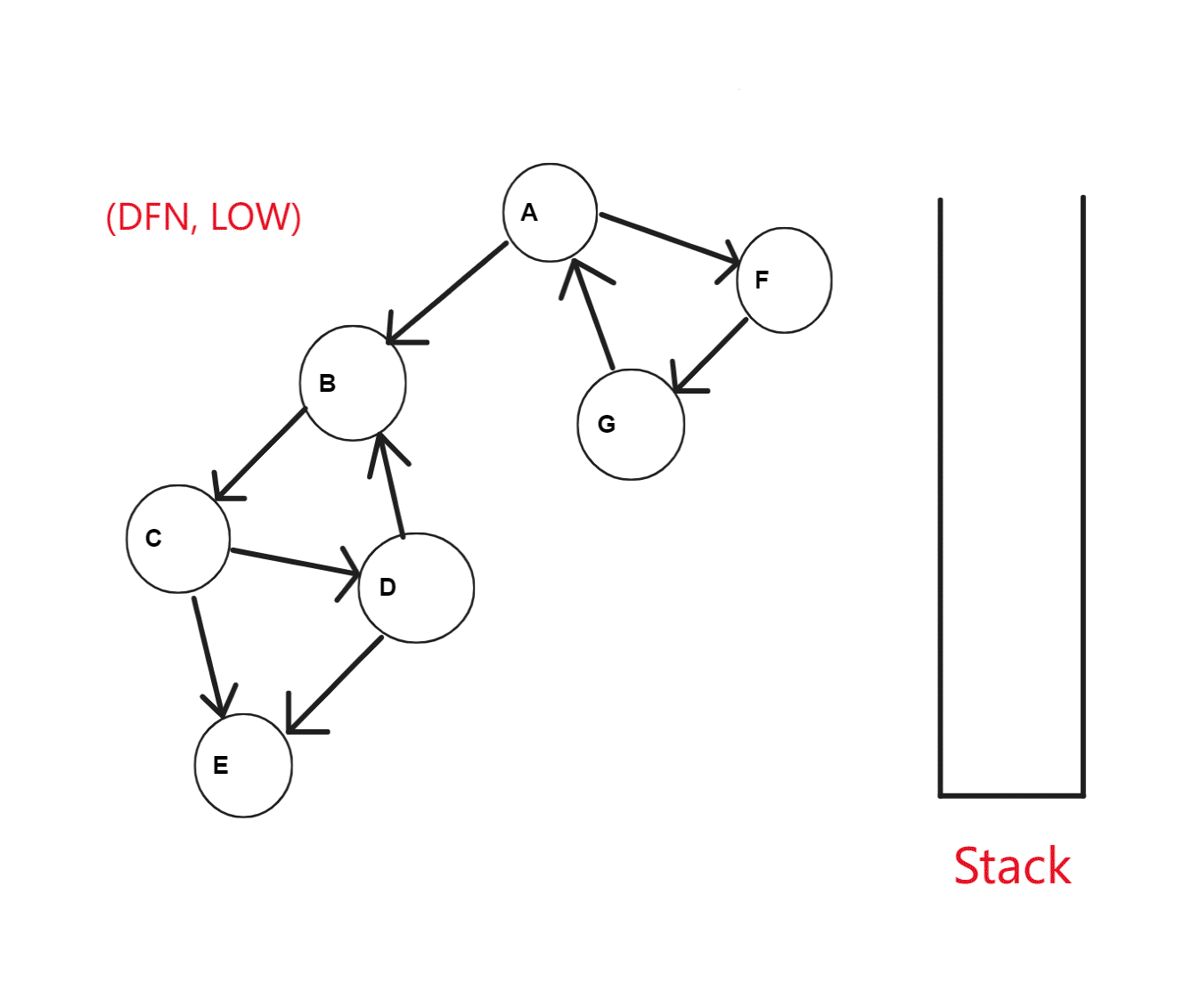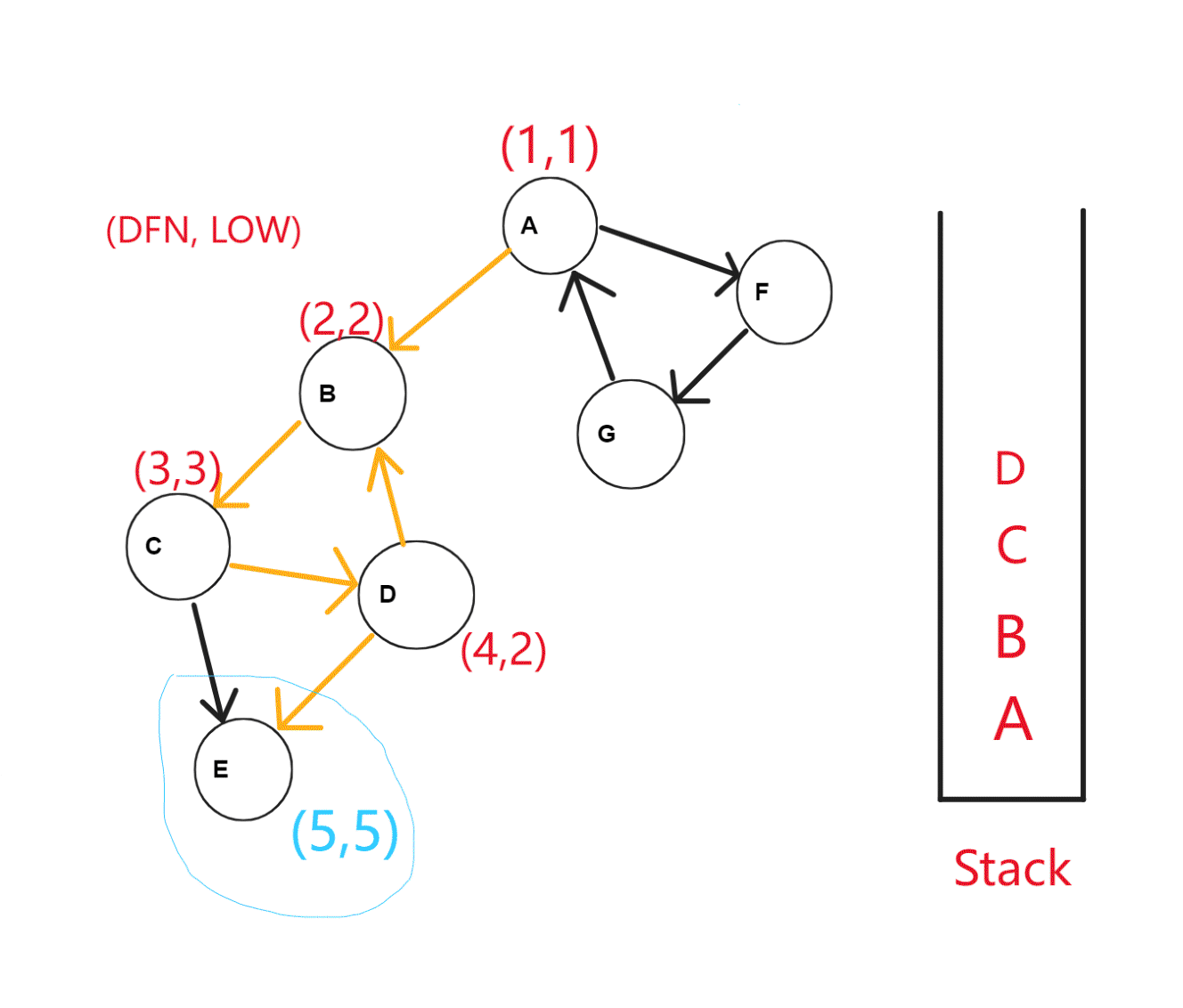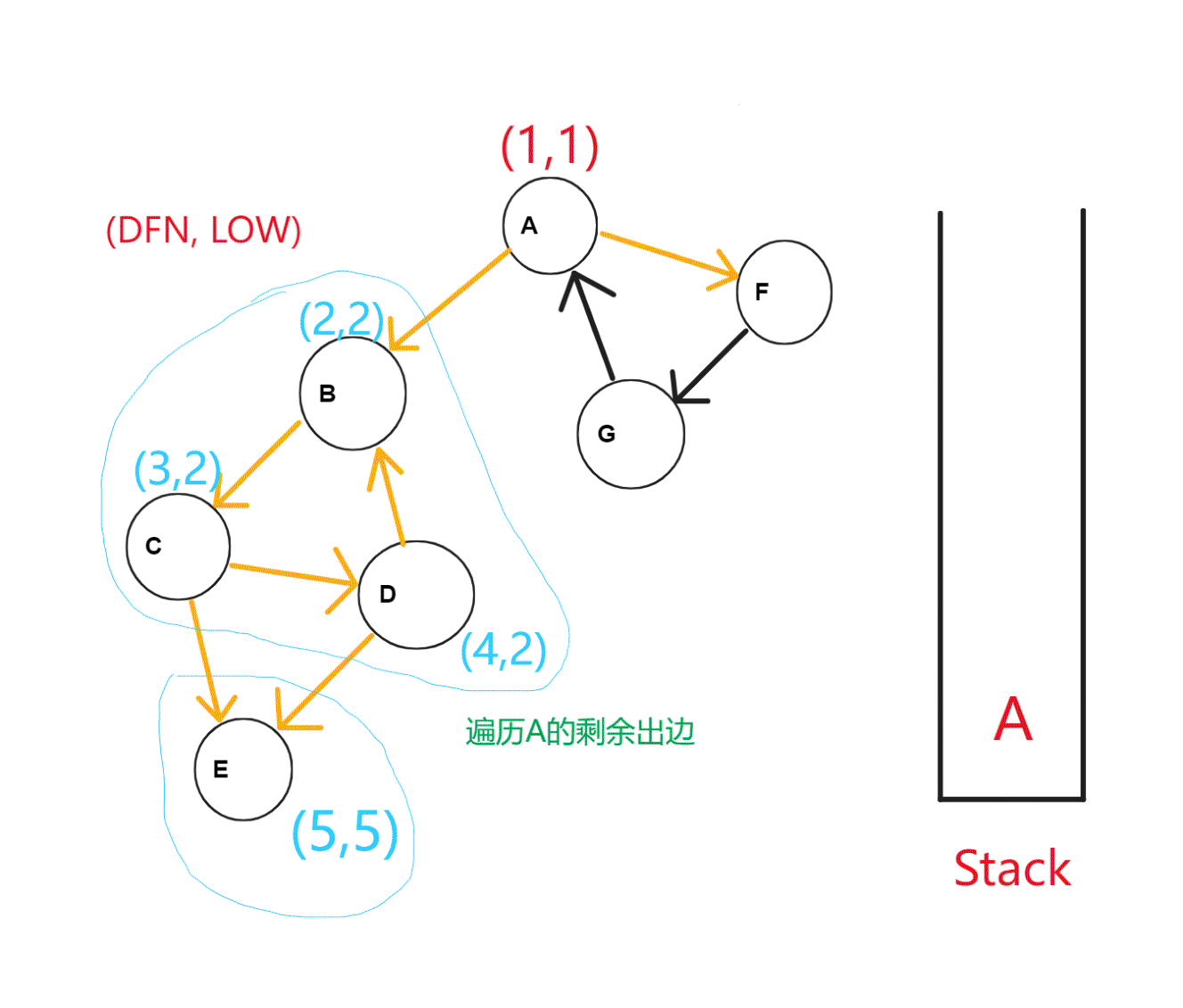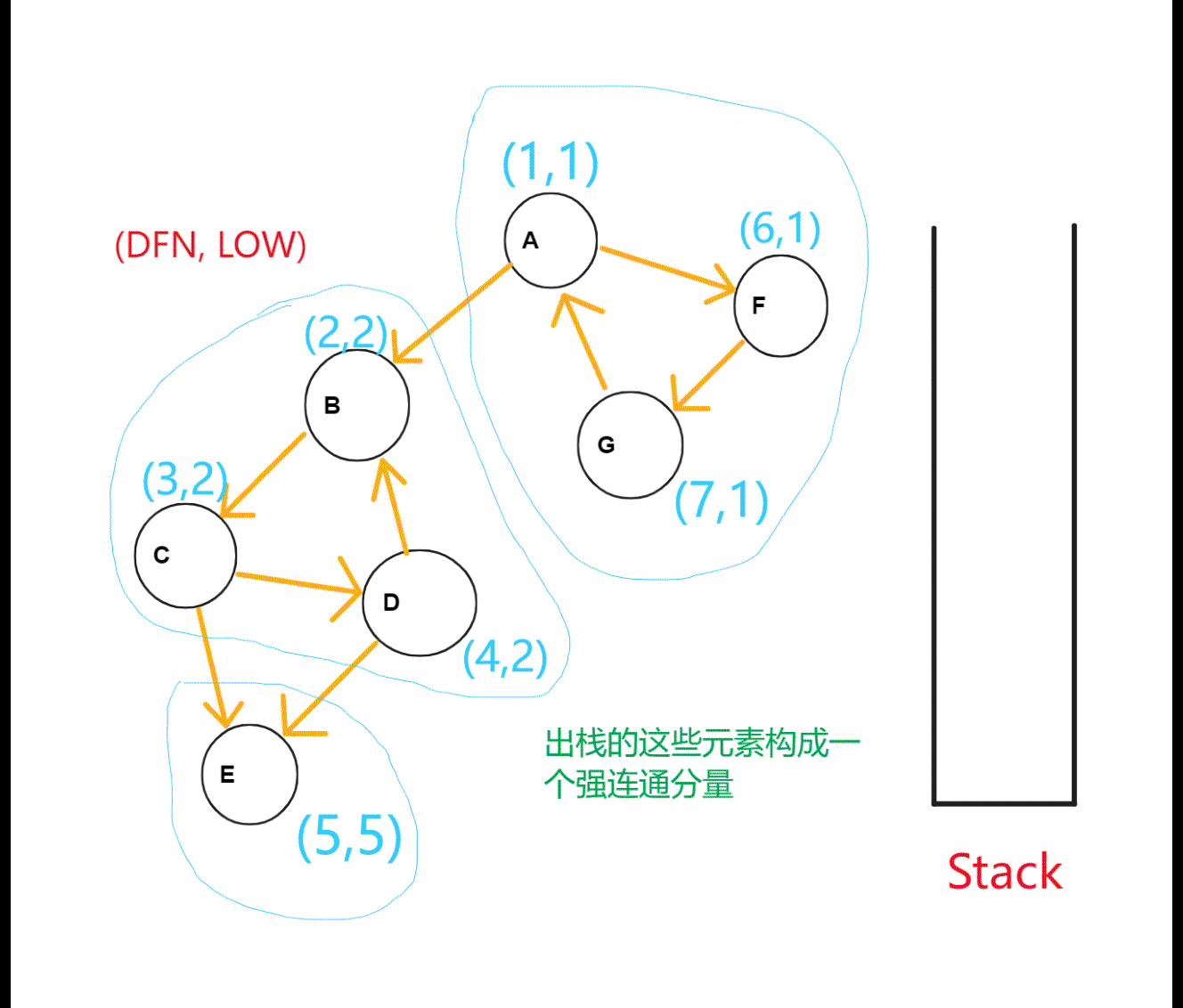
那么,对于第一个被强连通分量访问到的节点而言,存在 \(dfs_u=low_u\),而且一个强连通分量中尤其只有一个这样的点。
三、例题讲解
说是讲解,其实挺惭愧,被板子题肘击了。
1. 题面
P3387 【模板】缩点
题目描述
给定一个 \(n\) 个点 \(m\) 条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。
输入格式
第一行两个正整数 \(n,m\)。
第二行 \(n\) 个整数,其中第 \(i\) 个数 \(a_i\) 表示点 \(i\) 的点权。
第三至 \(m+2\) 行,每行两个整数 \(u,v\),表示一条 \(u\rightarrow v\) 的有向边。
输出格式
共一行,最大的点权之和。
输入输出样例 #1
输入 #1
2 2
1 1
1 2
2 1
输出 #1
2
说明/提示
对于 \(100\%\) 的数据,\(1\le n \le 10^4\),\(1\le m \le 10^5\),\(0\le a_i\le 10^3\)。
- 2024-11-1 添加了 hack 数据;
2. 思路
大概就是用 Tarjan 将强连通图缩成一个点,毕竟这些点互相可达,就像你拿到某国的护照就可以去这个国家任意一个省份是一个道理,没必要再看点了。这样会剩下不少时间。
然后关于求最大点值,这里采用拓扑排序,套用 DP,就能做出来了。
这个主包讲的不错:更好的讲解
3. 代码
写的很烂,批判性参考。
#include <iostream>
#include <cstdio>
#include <vector>
#include <stack>
#include <queue>
#define int long long
using namespace std;
const int MAXN=1e5+5;
bool check(int);
void tarjan(int);
void topsort();
vector<int> g[MAXN],G[MAXN];
int indeed[MAXN],belong[MAXN];
int a[MAXN],u[MAXN],v[MAXN];
int f[MAXN];
int n,m,ans;
signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=m;i++){cin>>u[i]>>v[i];g[u[i]].push_back(v[i]);}for(int i=1;i<=n;i++){if(!check(i)){tarjan(i);}}for(int i=1;i<=m;i++){int x=belong[u[i]],y=belong[v[i]];if(x!=y){// 顶点不同G[x].push_back(y);indeed[y]++;}}topsort();for(int i=1;i<=n;i++){ans=max(ans,f[i]);}cout<<ans;return 0;
}
stack<int> s;
bool book[MAXN];
int low[MAXN],dfn[MAXN];
int scc[MAXN];// 节点在强连通分量中的编号
int len[MAXN];// 这个强连通分量的大小
int dfncnt,size;
bool check(int u){return dfn[u];
}
void tarjan(int u){low[u]=dfn[u]=++dfncnt;// 赋 dfs 序编号 s.push(u);book[u]=true;// 在栈中for(auto v:g[u]){if(!dfn[v]){// 这个点没有遍历过 tarjan(v);low[u]=min(low[u],low[v]);}else if(book[v]){// 在栈中low[u]=min(low[u],dfn[v]); }}if(dfn[u]==low[u]){// 强连通分量的起始点 ++size;while(true){int t=s.top();s.pop();scc[t]=size,book[t]=false;belong[t]=u;// 链接点 len[size]++;if(t==u){break;}a[u]+=a[t];// 缩点 }}
}
queue<int> q;
void topsort(){// 拓扑排序for(int i=1;i<=n;i++){if(i==belong[i]&&!indeed[i]){q.push(i);f[i]=a[i];}}while(!q.empty()){int u=q.front();q.pop();for(auto v:G[u]){f[v]=max(f[v],f[u]+a[v]);indeed[v]--;if(!indeed[v]){q.push(v);} }}
}
