AI学习日记 - 实践
目录
一、决策树
1.定义
2.算法步骤
(1)特征选择
(2)节点分裂
(3)递归停止条件
(4)剪枝处理
3.特殊特征
(1)独热编码
(2)连续值特征
二、熵
1.定义
2.公式
3.信息增益
总结
一、决策树
1.定义
决策树是一种基于树状结构的监督学习算法,用于分类和回归任务。通过递归划分数据集,决策树模拟人类决策过程,每个内部节点代表一个特征判断,分支代表判断结果,叶节点代表最终预测类别或数值。
适用场景:结构化数据(不适用于处理图片,音频,文本等非结构化信息)
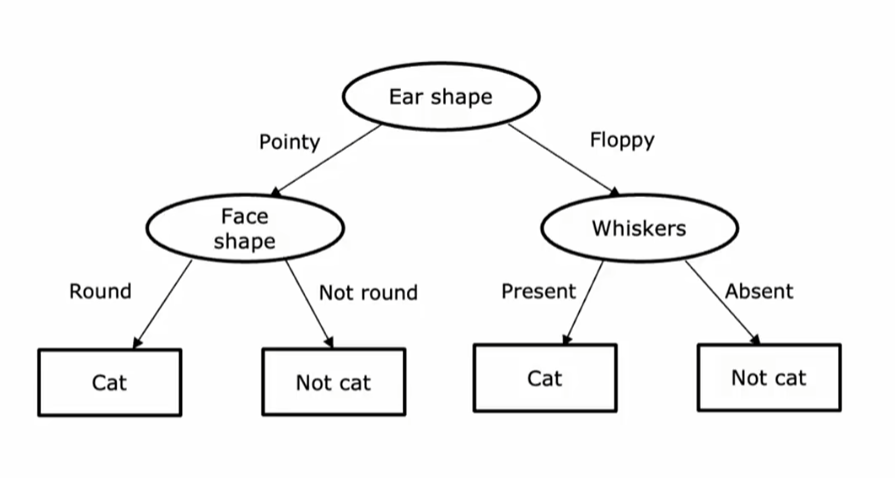
2.算法步骤
(1)特征选择
根据算法(如信息增益、基尼指数)选择能获得纯度最高的子集作为最佳划分特征。
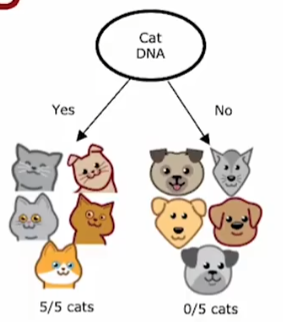
例1,就是:以下四个特征中,选择catdna是作为特征得到的结果纯度最高。有dna的全是猫,没有dna的全不纯度拉满!
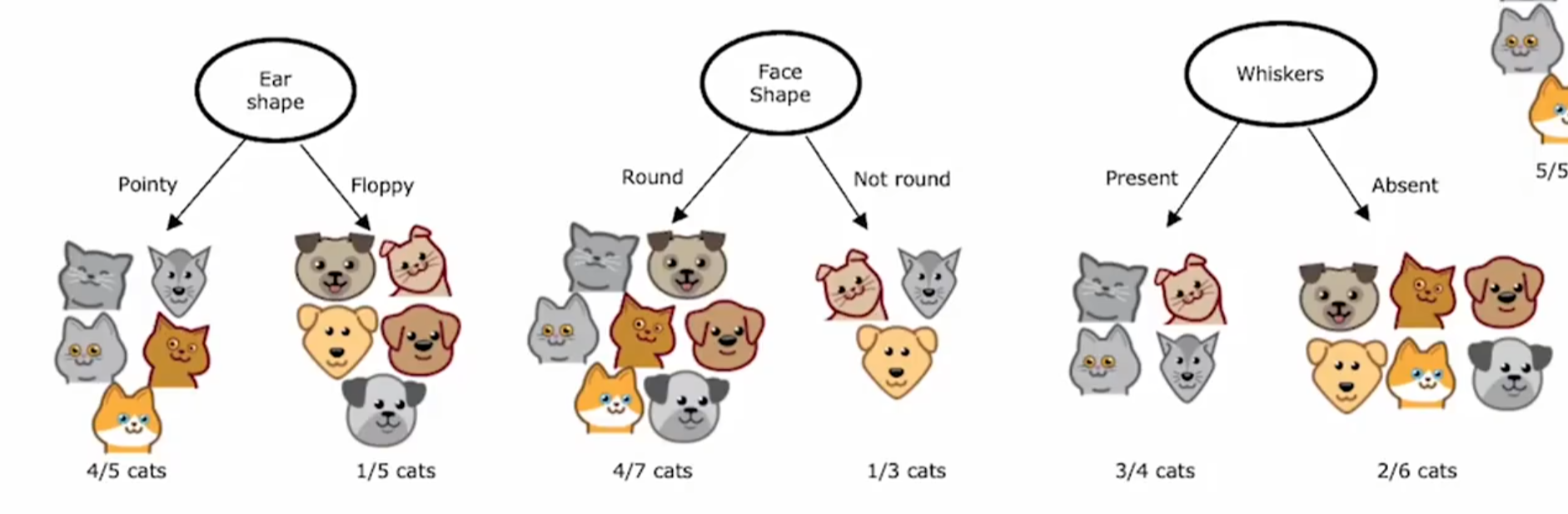
(2)节点分裂
将材料集按特征值划分为子集,生成分支。
(3)递归停止条件
- 节点样本属于同一类别。(如例1中的catdna)
- 超过设定深度
- 无剩余特征或样本数低于阈值。
(4)剪枝处理
凭借预剪枝(限制树深度)或后剪枝(代价复杂度剪枝)防止过拟合。
3.特殊特征
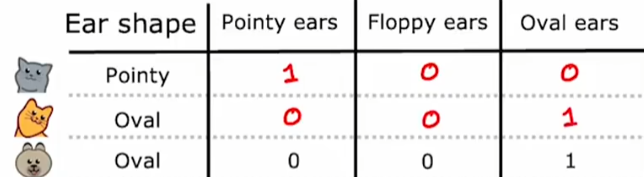
(1)独热编码
决策树无法直接处理在二分类以上的特征(比如耳朵形状有三种),需凭借独热编码(热=1)转换为数值形式。将具有k个类别的特征展开为k个二进制列,每列对应一个类别值,样本属于该类别则标记为1,否则为0。
(2)连续值特征
决策树的特征不再是非0即1,而是从一个特定的区间取值(比如体重15kg),尝试选定不同的阈值(体重<=8),计算信息增益公式来获取信息增益最大的阈值。
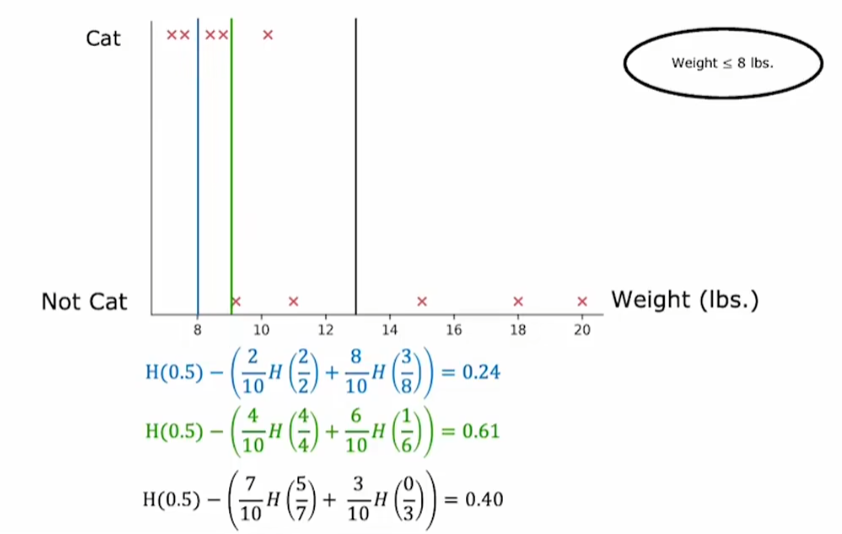
二、熵
1.定义
熵(Entropy)是信息论中的核心概念,用于衡量系统的不确定性或混乱程度。
在决策树中用于评估材料集的纯度(特征选择)。熵值越高,数据的不确定性越大;熵值越低,数据的纯度越高。
熵=不纯度
2.公式
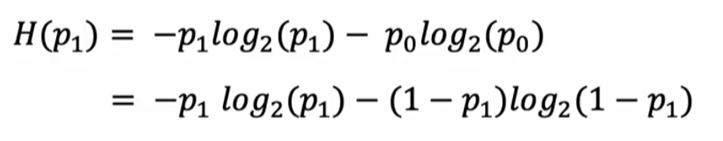
- H(p1) 表示数据集p1 的熵
- 猫概率,p1为非猫概率)就是p0=1-p1(p0为
log以2为底是为了刚好峰值是1
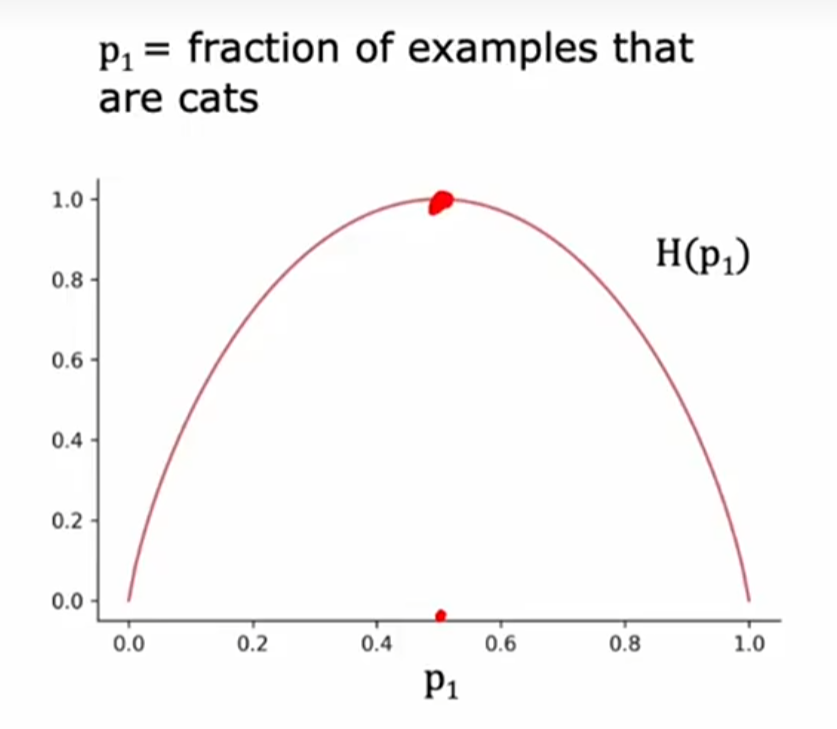
例2:当数据集中一半猫一半狗,混乱程度最大,H(p1)=1;反之材料集要是只有猫或只有狗,H(p2)=0,混乱程度最小

3.信息增益
信息增益是决策树算法中用于选择最优划分特征在选择分裂某个特征时,素材集就是的算法,基于熵(Entropy)概念。它衡量的混乱性(熵)减少的程度。信息增益越大,意味着使用该属性进行划分能带来更多的信息量,从而更有效地分类资料。
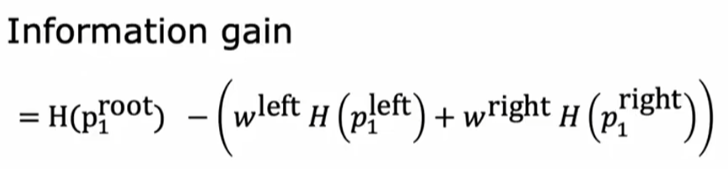
用父节点的熵 -左右子节点的熵的加权和= 混乱性(熵)减少的程度
例3:父节点共有十个样本,五猫五狗,H(5/10)=1。左右子节点按照有无胡须划分,左边三猫一狗,右边2猫4狗,所以分别是H(3/4)和H(2/6)。按照加权求和即使按照子节点分得的样本数加权,左边四只有胡须的,右边六只有胡须的,所以是4/10H(3/4)+6/10H(2/6)。最终我要计算他的熵减少的程度:H(5/10)-( 4/10H(3/4)+6/10H(2/6))
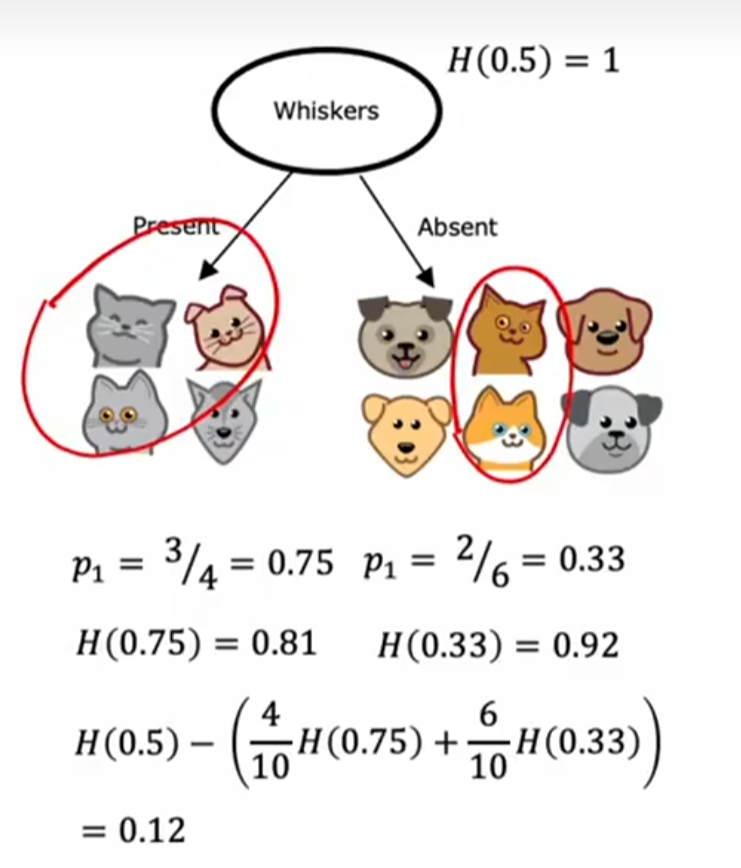
总结
本文介绍了决策树算法的首要过程,详细聚焦于特征选择于递归停止条件,并且引入了熵的概念从而引出信息增益的公式,此外还简单提及了一些特殊特征取值的处理方式