Learning Continuous Image Representation with Local Implicit Image Function

Learning Continuous Image Representation with Local Implicit Image Function

LIIF：利用INR实现任意倍数的超分。
代码仓库

动机

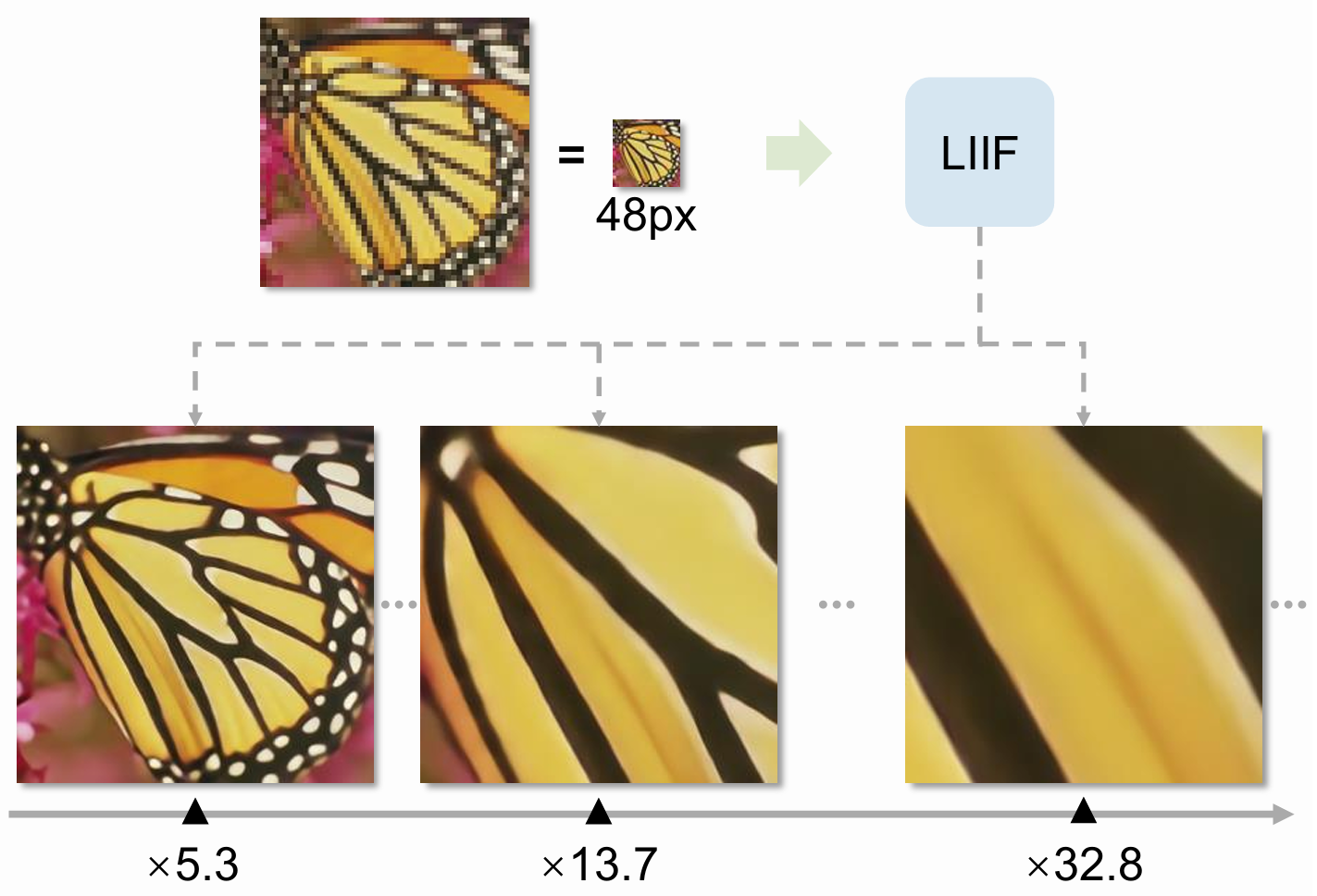
学习一个从坐标值到RGB值的映射，从而实现任意倍数的超分。

方法

局部隐式图像函数

本文目标为将隐向量\(z\)、坐标\(x\)映射为信号（RGB）\(s\)：\(s=f_{\theta}(z,x)\)。其中，坐标是连续的，即目标是拟合一副连续的图像。

由于真实图像只存储了有限的像素点，所以连续图像位置\(x_q\)处的像素值由离散图像上的最近邻\(v^*\)及其对应的隐向量（特征向量）\(z^*\)得到：\(I^{(i)}(x_q)=f_\theta(z^*,x_q-v^*)\)。

特征展开

显然，单点的特征组成的特征图\(M^{(i)}\)精度有限，所以用周围\(3 \times 3\)邻域特征的级联进行替换：

\[\hat{M}^{(i)}_{jk}={Concat}(\{ M^{(i)}_{j+l,k+m} \}_{l,m\in{-1,0,1}}) \]

局部编码

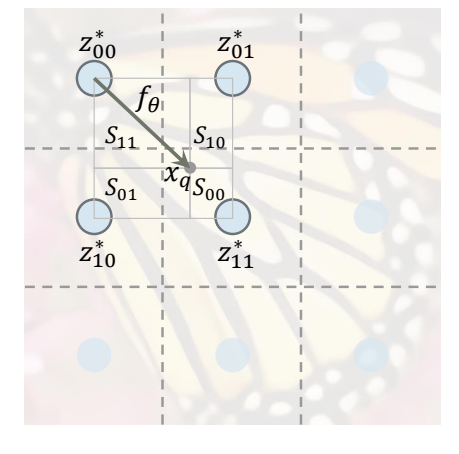
最近邻这种方法比较离散，在边界处选取的点会突变。因此本文使用周围四点的欧氏距离加权平均实现：

\[I^{(i)}(x_q)=\sum_{t\in \{ 00, 01, 10, 11\}}\frac{S_t}{S} \cdot f_\theta(z_t^*,x_q-v_t^*) \]

单元解码

虽然通过坐标能够直接得到HR图像对应的像素值，但是这样没有考虑放大倍数。因此将放大倍数也作为输入进行控制：

\[s=f_{cell}(z, [x,c]) \]

其中，\(c\)具体为查询的信号对应的区域大小\([c_h, c_w]\)。该函数可以理解为：查询连续图像\(x\)位置上，大小为\(c\)对应区域的像素值。

训练

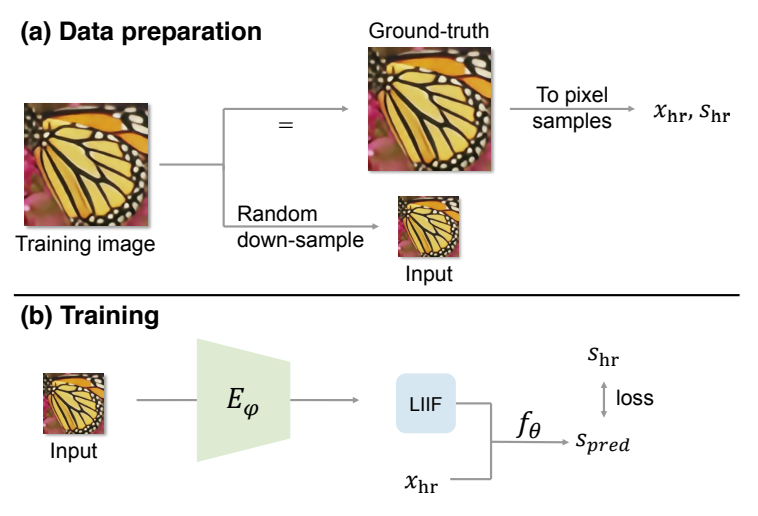
• 将输入图像随机倍数下采样获得输入。输入经过编码器得到二维特征图。
• 通过本文的模块与坐标值预测HR（高分辨率）上的像素值，与GT作损失（本文用L1）。

实验

在任意倍数超分上性能达到SOTA，有良好的视觉效果。

单元解码确实能够控制获得的像素对应区域。在\(c\)取值较大时，能够形成类似马赛克的模糊效果。相比于不使用单元更清晰。

总结

本文利用近邻特征及坐标偏移计算连续坐标上的颜色值。某种程度上相当于“高级插值”，只是这一“插值”是通过特征映射到连续图像域\(f_\theta\)上实现。本文巧妙地用隐式神经表示实现了连续图像上的采样与插值过程。不过若严格一点考虑，\(f_\theta\)的输入是特征向量、坐标偏移量、放大倍数，相当于对特征进行了有条件的解码，和一般的图像重建INR有些许的差异。