1.
U612392 追忆
是一个小技巧
考虑在序列中尽量向前匹配,在那个位置计数
然后发现要求是对于一个元素,在其前面的元素与其之间的空隙不能有这个字符
所以可以枚举结尾位置
通过 $\sum _{i = 0}^n \binom{i - n - 1}{n - 1} \times 26^{n + k - i} \times 25^{i - n} $
简单计算即可
AC
2.
P11390 [COCI 2024/2025 #1] 教师 / Učiteljica
想到枚举右端点,然后统计和法左端点
\(k = 1\)
维护每种数的合法区间
然后相当于求非零位置和
是区间加和非 0 位置个数
把右端点看成 x 轴,合法左端点放到 y 轴上,其实就是一个简单的扫描线模版,不用离散化
有两种解决方案
-
维护最小值及其个数
-
维护区间覆盖次数
我写的第一种
\(k > 1\)
考虑其实是要求每种 k 都出现,相当于是求交集,不好写,转换成求并集容斥就行
复杂度 \(O(2^k \times k \times n \log n)\)
这个容斥的原理和并集转换是一样的
用二项式定理可以简单证明
AC
3.
P4922 [MtOI2018] 崩坏3?非酋之战!
前言
这是一篇 \(O(n)\) 的题解
NOIP 模拟赛放了这道题目
个人认为还是较为简单的
赛时思路完整推导
读完题目,发现没有关于时间的最优化,所以可以发现其实技能的很大一部分是被其他技能单调的
-
闪避不如大招
-
爱酱的炸弹不如技能
-
犹大的誓约不如大招
其实时间暂停和减速都是 buff 在打伤害
-
奥托之光由于清除 buff,没用
-
律者之力不如大招
所以其实有用的技能只有 3 个
-
大招用于时间暂停 5s
-
技能用于获得 1 层燃烧 buff
-
分支攻击用于减速
此时设 dp[i][j] 表示当前有 \(i\) 层燃烧 buff , \(j\) 层减速的最大攻击值
直接每次转移三个技能就是 \(O(n^3)\)
for(int j = 0;j <= i;j ++) {for(int k = 0;k <= i - j;k ++) {if(f[j][k] == -inf) continue;int h = f[j][k] + (j + 1) * k * atk;g[j][k] = max(g[j][k] , h + 5 * k * atk + 12 * atk);g[j + 1][k] = max(g[j + 1][k] , h + 7 * atk);g[j][k + 1] = max(g[j][k + 1] , h + 8 * atk);}
}
然后 \(n^2\) 的解法就是通过分析大招与技能 / 大招与分支攻击的最优相对关系
(可以自己设当前有几层燃烧 buff和减速 buff ,然后列关系式)
分析出大招在最后更优
这样 dp 过程中只需要维护两个 buff , 然后每次最后的大招伤害可以 \(O(1)\) 计算
复杂度到了 \(O(n^2)\),已经可以通过了
然而我们可以继续剖析题目性质
我有两个猜测
-
三个技能是有顺序的,大概为燃烧,减速,大招
-
当 n 很大时显然主要靠燃烧 buff 打伤害
想到这里时 我们不想思考,可以打个表
#include<bits/stdc++.h>
#define int long long
using namespace std;template <typename T>
void _debug(const T& t) { std::cerr << t << '\n'; }
template <typename T, typename... Args>
void _debug(const T& t, const Args&...res) { std::cerr << t << ' '; _debug(res...); }
#define debug(...) _debug(#__VA_ARGS__ " =", __VA_ARGS__)const int N = 1e4 + 10 , inf = 1e18;
int n , hp , atk;
int f[1010][1010] , g[1010][1010] , pr[200][200][200];
void fa(int i) {debug(f[0][0]);int x = 0 , y = 0;for(int j = 0;j <= i;j ++)for(int k = 0;k <= i - j;k ++) if(f[j][k] > f[x][y]) x = j , y = k;debug(x , y , f[x][y]);for(int j = i;j >= 1;j --) {debug(j , x , y , pr[j][x][y]);if(pr[j][x][y] == 2) x --;else if(pr[j][x][y] == 3) y --;else if(!pr[j][x][y]) { cout << "WAWAWA---\n"; exit(0); }}
}signed main() {
// freopen("c1.in","r",stdin);
// freopen("c.out","w",stdout);cin >> n >> hp >> atk; atk /= 10;for(int j = 0;j <= n;j ++)for(int k = 0;k <= n;k ++) g[j][k] = -inf;g[0][0] = 0;for(int i = 0;i <= n;i ++) {int mx = 0;for(int j = 0;j <= i;j ++)for(int k = 0;k <= i - j;k ++) f[j][k] = g[j][k] , mx = max(mx , f[j][k]);if(mx >= hp) { fa(i); cout << i << '\n' << "LeiZeProMax Nb!!!"; return 0; }if(i == n) { fa(i); cout << mx << '\n' << "hks"; return 0; }for(int j = 0;j <= i + 1;j ++)for(int k = 0;k <= i + 1 - j;k ++) g[j][k] = -inf;if(i == 30) debug(f[15][15] , g[15][15]);for(int j = 0;j <= i;j ++) {for(int k = 0;k <= i - j;k ++) {if(f[j][k] == -inf) continue;int h = f[j][k] + (j + 1) * k * atk;if(h + 5 * k * atk + 12 * atk >= g[j][k]) pr[i + 1][j][k] = 1;g[j][k] = max(g[j][k] , h + 5 * k * atk + 12 * atk);if(h + 7 * atk >= g[j + 1][k]) pr[i + 1][j + 1][k] = 2;g[j + 1][k] = max(g[j + 1][k] , h + 7 * atk);if(i == 29 && j == 14 && k == 15) debug(g[j + 1][k] , pr[i + 1][j + 1][k]);if(h + 8 * atk >= g[j][k + 1]) pr[i + 1][j][k + 1] = 3;g[j][k + 1] = max(g[j][k + 1] , h + 8 * atk);if(i == 29 && j == 15 && k == 14) debug(g[j][k + 1] , pr[i + 1][j][k + 1]);}}}return 0;
}
打出来发现
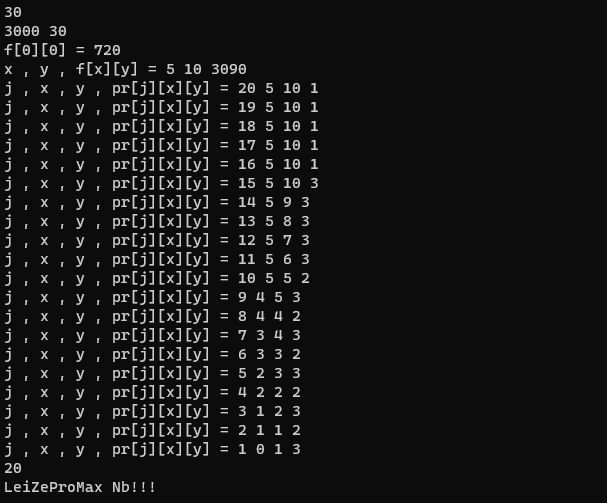
看最后一列是转移点
发现是 燃烧减速交错 ?
不对结尾处不同,多打几个发现最后 10 个其实是固定的
所以程序告诉我们答案是 先燃烧减速交错,后 10 个直接叠 5 层减速,最后 5 个用大招
分析原因的话用上面第二个猜测,我们可以考虑只 buff 的伤害, 设当前有 x 层减速, y 层燃烧
则下一次打的伤害即为 \(x \times y\) ,由初中奥数可得,当 \(x + y\) 一定, \(x = y\) 时 \(x \times y\) 最大
所以可得大部分是减速燃烧交错叠加
至于最后的特殊情况,其实也是好感性考虑的
减速其时是为后面每一次都增加 1 秒的攻击事件,是永久的
而大招暂停 5 秒是为当前轮增加 5 秒的攻击事件,是暂时的
从长远来看,我们当然是选择减速,但当后缀攻击次数小于 5 时,暂时性的大招反而具有优势
大招前叠 5 次燃烧,其实也是为了和后面的大招凑平方数
所以如果大招暂停时间更长,其后面的特殊情况的长度也会对应线性增长
至此就没了
代码
代码直接按上面的结论打即可,应该挺短的,注意长度不足 10 的情况
跑到了最优解,不卡常比非线性做法第一名快了 5 倍,线性做法不就应该比平方做法快吗?
下面是我赛时代码,可以参考结构 ?
注意输出的字符串不同
#include<bits/stdc++.h>
#define int long long
using namespace std;template <typename T>
void _debug(const T& t) { std::cerr << t << '\n'; }
template <typename T, typename... Args>
void _debug(const T& t, const Args&...res) { std::cerr << t << ' '; _debug(res...); }
#define debug(...) _debug(#__VA_ARGS__ " =", __VA_ARGS__)const int N = 1e4 + 10 , inf = 1e18;
int n , hp , atk;
int f[1010][1010] , g[1010][1010];
int col[N];
bool check(int x , int y , int mx) {for(int i = 1;i <= 5;i ++) {mx += (x + 1) * y * atk + 8 * atk , y ++;if(mx >= hp) return 1;}for(int i = 1;i <= 5;i ++) {mx += (x + 6) * y * atk + 12 * atk;if(mx >= hp) return 1;}return 0;
}
void dp(int len) {for(int j = 0;j <= len;j ++)for(int k = 0;k <= len;k ++) g[j][k] = -inf;g[0][0] = 0;for(int i = 0;i <= len;i ++) {int mx = 0;for(int j = 0;j <= i;j ++)for(int k = 0;k <= i - j;k ++) f[j][k] = g[j][k] , mx = max(mx , f[j][k]);if(mx >= hp) { cout << i << '\n' << "Tech Otakus Save The World!"; exit(0); }for(int j = 0;j <= i + 1;j ++)for(int k = 0;k <= i + 1 - j;k ++) g[j][k] = -inf;for(int j = 0;j <= i;j ++) {for(int k = 0;k <= i - j;k ++) {if(f[j][k] == -inf) continue;int h = f[j][k] + (j + 1) * k * atk;g[j][k] = max(g[j][k] , h + 5 * k * atk + 12 * atk);g[j + 1][k] = max(g[j + 1][k] , h + 7 * atk);g[j][k + 1] = max(g[j][k + 1] , h + 8 * atk);}}}
}signed main() {cin >> n >> hp >> atk; atk /= 10;if(!hp) { cout << 0 << '\n' << "Tech Otakus Save The World!"; return 0; }if(n <= 300) {for(int j = 0;j <= n;j ++)for(int k = 0;k <= n;k ++) g[j][k] = -inf;g[0][0] = 0;for(int i = 0;i <= n;i ++) {int mx = 0;for(int j = 0;j <= i;j ++)for(int k = 0;k <= i - j;k ++) f[j][k] = g[j][k] , mx = max(mx , f[j][k]);if(mx >= hp) { cout << i << '\n' << "Tech Otakus Save The World!"; return 0; }if(i == n) { cout << mx << '\n' << "MiHoYo Was Destroyed!"; return 0; }for(int j = 0;j <= i + 1;j ++)for(int k = 0;k <= i + 1 - j;k ++) g[j][k] = -inf;for(int j = 0;j <= i;j ++) {for(int k = 0;k <= i - j;k ++) {if(f[j][k] == -inf) continue;int h = f[j][k] + (j + 1) * k * atk;g[j][k] = max(g[j][k] , h + 5 * k * atk + 12 * atk);g[j + 1][k] = max(g[j + 1][k] , h + 7 * atk);g[j][k + 1] = max(g[j][k + 1] , h + 8 * atk);}}}return 0;}else {dp(10);for(int i = 1;i <= n - 10;i ++) {if(i & 1) col[i] = 3;else col[i] = 2;}for(int i = n - 9;i <= n - 5;i ++) col[i] = 3;for(int i = n - 4;i <= n;i ++) col[i] = 1;int x = 0 , y = 0 , mx = 0;for(int i = 1;i <= n;i ++) {int adv = 0;if(col[i] == 1) adv = (x + 6) * y * atk + 12 * atk;else if(col[i] == 2) adv = (x + 1) * y * atk + 7 * atk , x ++;else adv = (x + 1) * y * atk + 8 * atk , y ++;if(mx >= hp - adv) break;mx = mx + adv;if(i == n) { cout << mx << '\n' << "MiHoYo Was Destroyed!"; return 0; }}x = 0 , y = 0 , mx = 0;for(int i = 1;i <= n - 10;i ++) {
// debug(x , y , mx , check(x , y , mx));int adv = 0;if(i & 1) adv = (x + 1) * y * atk + 8 * atk , y ++;else adv = (x + 1) * y * atk + 7 * atk , x ++;mx += adv;if(check(x , y , mx)) { cout << i + 10 << '\n' << "Tech Otakus Save The World!"; return 0; }
// debug(i , mx);}
// cout << "hhh";}return 0;
}
后记
由于作者本人很懒还有点笨,所以这是作者第一篇题解,如果有问题可以私信联系,感谢 ~~
乐一下
搬题时同学把题面改成关于吕布的,
玩过农的都知道,吕布只有 3 个技能,一个一技能附魔(挂 buff),二技能减速,还有大招(血条再厚,一刀带走)
还是写实
4.
P12336 第三心脏
逆天改造
先推柿子
$ \sqrt{a^2 + b^2 + c^2 + d^2} = a \oplus b \oplus c \oplus d $
$ a^2 + b^2 + c^2 + d^2 = (a \oplus b \oplus c \oplus d)^2 \ge d^2 = (d + x)^2 $
拆开得
$ a^2 + b^2 + c^2 + d^2 = (d + x) ^ 2$
\(a^2 + b^2 + c^2 = 2 \times d \times x + x^2\)
\((a \oplus b \oplus c \oplus d)^2 = (d + x) ^ 2\)
\(a \oplus b \oplus c \oplus d = d + x\)
合起来即为
设 x 最高位为 p , 我们让 d 的 \(\le p\) 位,直接可以得到
然后我让 x = 1 ,后面的构造可以看出对任意 x 都可以构造
让 \(b = 2^p + a , c = 2^p + 2^{p + 1} + 1\)
发现成立,
但当 a 为奇数时, \(d \equiv 0 (\bmod 2)\) 不成立
微调一下 \(b = 2^p + a - 1 , c = 2^p + 2^{p + 1}\) 即可
AC
